

La distorsione è una alterazione della forma del segnale di uscita di un quadripolo rispetto al segnale di ingresso.
Un errore grave, sintomo di non comprensione dell'argomento: confondere la distorsione con il rumore.
La figura di apertura ovviamente non ha nulla a che fare con i contenuti di questa pagina.
Un quadripolo ideale deve avere distorsione nulla, cioè il segnale di uscita deve avere la stessa forma del segnale di ingresso, sia nel dominio del tempo che in quello della frequenza:
Non costituisce distorsione:
In genere la presenza di una distorsione è considerata un difetto del quadripolo; esistono però circuiti o applicazioni in cui la distorsione è voluta; per esempio:
Le distorsioni vengono classificate confrontando lo spettro del segnale di ingresso con lo spettro del segnale di uscita:
In un circuito reale possono essere presenti contemporaneamente entrambi i tipi di distorsione.
In un circuito reale, oltre alle distorsioni, è presente anche il rumore.
La distorsione di ampiezza è una distorsione lineare presente in quadripoli il cui guadagno G dipende dalla frequenza (nota 6).
Il grafico che meglio mette in evidenza la distorsione di ampiezza è la risposta in frequenza. Essa rappresenta, per un segnale sinusoidale, il modulo del guadagno in dB in funzione della frequenza su scala logaritmica. Se un quadripolo è privo di distorsione di ampiezza questo grafico appare come una linea orizzontale, cioè il guadagno è costante per tutte le frequenze.
Tale distorsione può essere presente in tutti i circuiti, lineari e non lineari.
Essa non è osservabile se in ingresso è presente una singola sinusoide (perché?).
Il grafico seguente mostra la risposta in frequenza di un quadripolo:
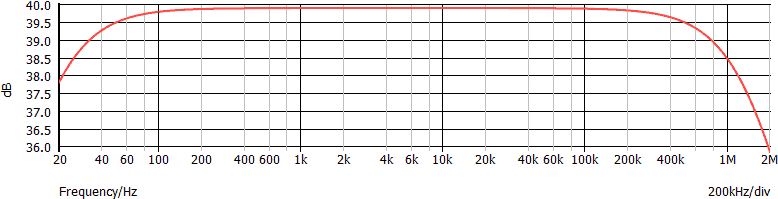
Questo quadripolo presenta un distorsione di ampiezza, non essendo la sua risposta in frequenza una linea orizzontale.
Si noti che tale comportamento è un difetto per gli amplificatori, ma la base del funzionamento dei filtri.
Per limitare gli effetti negativi della distorsione di ampiezza, il quadripolo dovrebbe essere utilizzato solo nell'intervallo di frequenze in cui il suo guadagno è costante: nell'esempio mostrato il guadagno è costante indicativamente tra 200 Hz e 100 kHz; in questo intervallo G vale poco meno di 40 dB.
La banda di un quadripolo è l'intervallo di frequenze entro cui il guadagno è sufficientemente costante. La definizione di "sufficientemente" dipende dal''applicazione e valori spesso utilizzati sono ±3 dB oppure ±1 dB. Per esempio, in riferimento al grafico, possiamo indicare come banda a -1 dB l'intervallo tra 30 Hz e 800 kHz.
Consideriamo un quadripolo con guadagno di tensione:
L'ingresso del quadripolo è costituito dalla somma di una sinusoide con frequenza 1 kHz ed una sinusoide con frequenza 2 kHz; per entrambe l'ampiezza è 1 V.
I due grafici seguenti, disegnati utilizzando un simulatore, mostrano ingresso (a sinistra, rosso) ed uscita (a destra, blu) nel dominio del tempo:

La seconda coppia di grafici mostra ingresso (a sinistra, rosso) ed uscita (a destra, blu) nel dominio della frequenza, rendendo più chiaro il legame tra guadagno e frequenza:

Il cambiamento nella forma dell'uscita rispetto all'ingresso è evidente sia nel dominio del tempo (manca la seconda "gobba") chi in quello della frequenza (il rapporto tra le linee spettrali è diverso).
Un segnale richiede sempre un tempo finito per passare dall'ingresso all'uscita di un quadripolo. Tale tempo può essere indicato come tempo di propagazione oppure ritardo di propagazione (Delay time, TD).
La distorsione da ritardo è una distorsione lineare presente in quadripoli il cui tempo di propagazione TD non è costante, ma dipende dalla frequenza.
Con qualche precisazione non discussa in questo contesto, tale distorsione può essere indifferentemente indicata come distorsione di fase (nota 2) o distorsione da ritardo di gruppo.
Tale distorsione può essere presente in tutti i circuiti, lineari e non lineari.
Essa non è osservabile se in ingresso è presente una singola sinusoide (perché?).
Il grafico seguente mostra il ritardo di propagazione di un quadripolo in funzione della frequenza del segnale sinusoidale in ingresso:
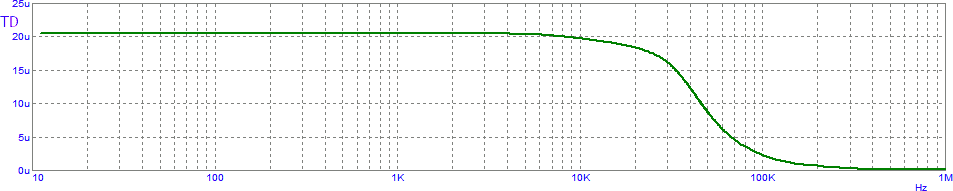
Questo quadripolo presenta un distorsione da ritardo, non essendo il suo tempo di propagazione costante.
Per limitare gli effetti negativi della distorsione di fase, questo quadripolo dovrebbe essere utilizzato solo nell'intervallo di frequenze in cui il suo ritardo di propagazione è costante, nell'esempio mostrato indicativamente fino a 4 kHz (TD = 20 µs) oppure oltre i 400 kHz (TD = 0).
I grafici seguenti mostrano ingresso ed uscita di un quadripolo con G = 10. Questo quadripolo:
Il segnale di ingresso è la somma di due sinusoidi con ampiezza 1 V e frequenze 1 kHz (porpora) e 2 kHz (verde):
Il quadripolo utilizzato come esempio, a causa del suo funzionamento non ideale:
Il guadagno è uguale per entrambe le sinusoidi (G = 10): il quadripolo quindi non introduce distorsioni di ampiezza.
Si vede chiaramente dal grafico ottenuto con un simulatore che l'uscita (secondo grafico, segnale rosso) ha cambiato forma rispetto al grafico dell'ingresso:
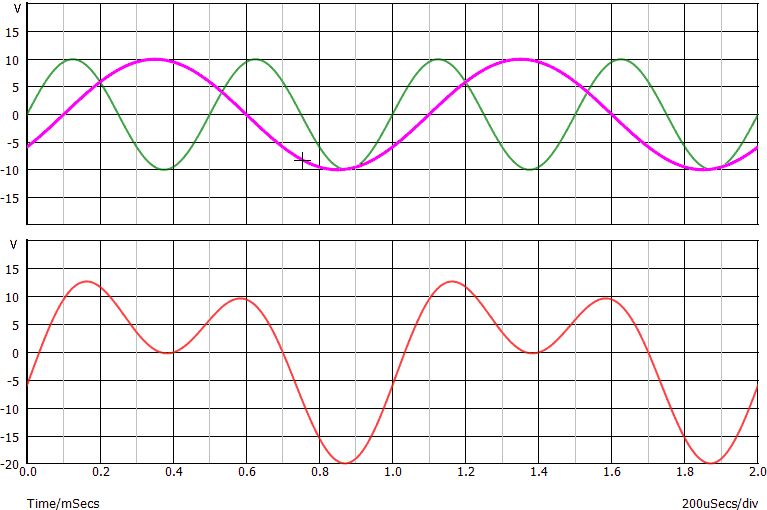
Si noti che, al contrario, le singole sinusoidi non hanno cambiato forma.
La distorsione armonica (Harmonic Distortion, HD) è una distorsione non lineare, tipica dei quadripoli non lineari (nota 7).
Un quadripolo presenta distorsione armonica se in presenza di un ingresso sinusoidale:
Le due definizioni esprimono esattamente lo stesso concetto (perché?).
Il nome distorsione armonica deriva dal fatto che i multipli interi della frequenza di una sinusoide sono spesso indicati col nome di armoniche, termine che deriva da contesti musicali.
Nei grafici seguenti sono mostrati ingresso ed uscita di un quadripolo che presenta distorsione armonica.
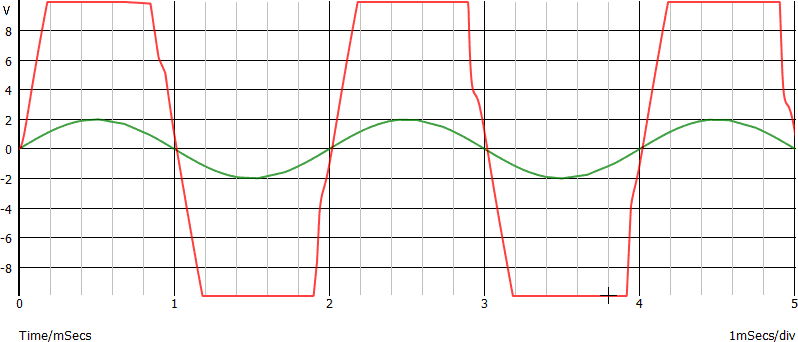
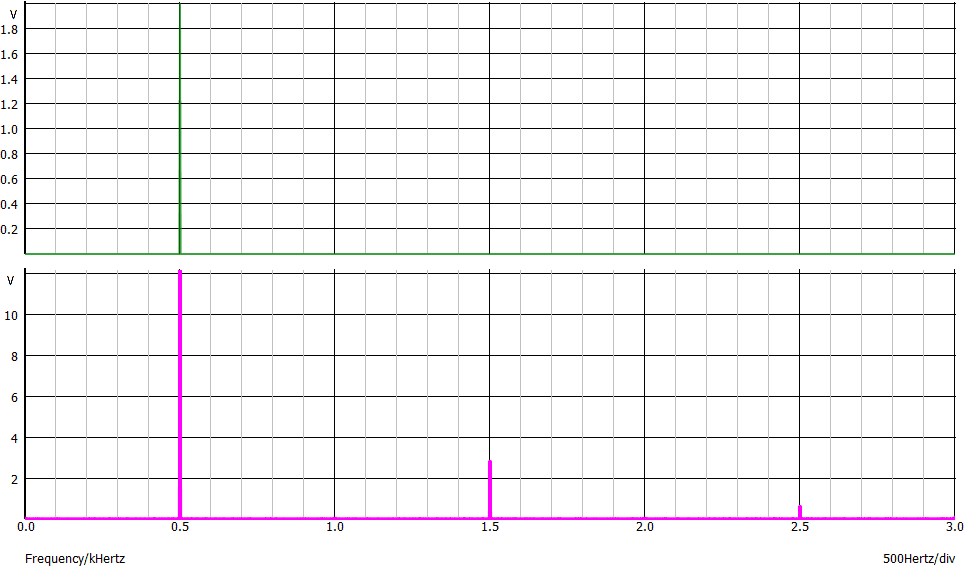
Da entrambi i grafici si osserva che la forma del segnale di ingresso (sinusoidale) è stata distorta diventando un segnale vagamente simile ad un'onda quadra.
Lo spettro del segnale di uscita spesso è disegnato con scala verticale logaritmica (o in dBV, cosa ovviamente equivalente) per poter meglio apprezzare le distorsioni introdotte dal quadripolo. Di seguito lo stesso grafico dell'esempio precedente con la tensione indicata in dBV. In questo grafico si vedono chiaramente le linee spettrali in corrispondenza dei tutte le armonica del segnale di ingresso, anche quelle che nel grafico su scala lineare non erano visibili perché troppo piccole.
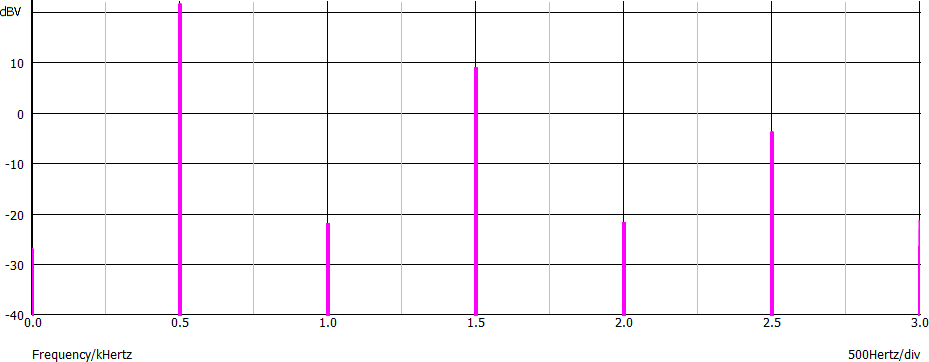
La distorsione da intermodulazione (Inter-Modulation Distortion, IMD) è una distorsione non lineare, tipica dei quadripoli non lineari. Essa si manifesta nei circuiti non lineari quando in ingresso sono presenti almeno due sinusoidi.
Se un quadripolo presenta questo tipo di distorsione, nell'ipotesi di ingresso costituito da due sole linee spettrali con frequenza f1 ed f2, in uscita sono presenti:
L'ingresso di un quadripolo che presenta IMD è costituito dalla somma di due sinusoidi con frequenza 3 kHz e 3.5 kHz.
In uscita avremo:
Di seguito la rappresentazione dell'ingresso (in rosso, in alto) e dell'uscita (in verde, in basso) nel dominio della frequenza:
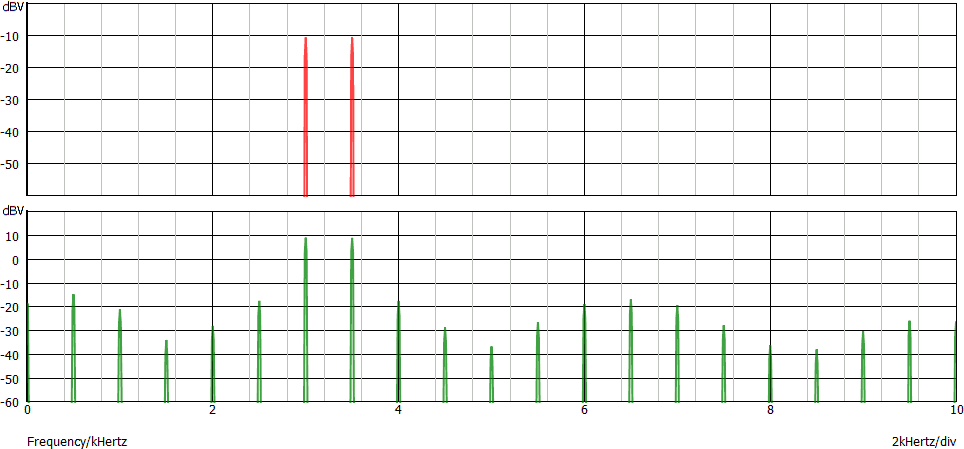
Nel dominio del tempo il grafico non è particolarmente significativo in quanto ingresso ed uscita appaiono praticamente uguali:
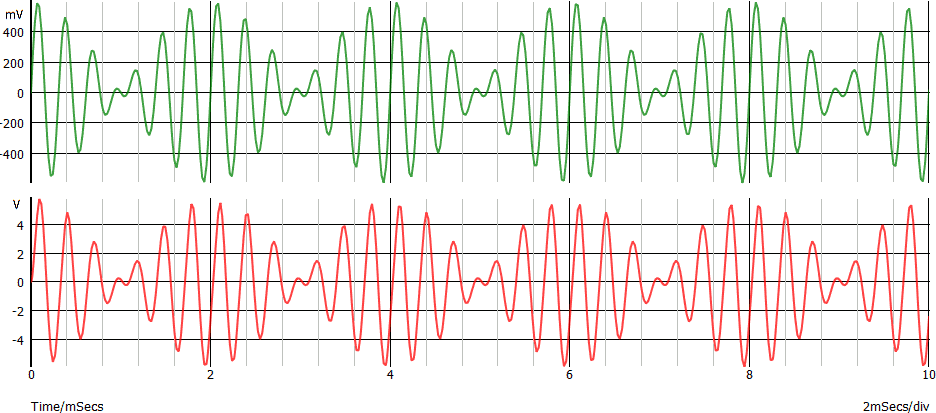
Due effetti della distorsione di intermodulazione (nota 3):
Le distorsioni da non linearità possono essere misurate attraverso numerosi metodi, spesso con definizioni piuttosto complesse e specialistiche. Sono qui ripostati solo due esempi, entrambi relativi ad un segnale di ingresso puramente sinusoidale:
La distorsione armonica totale (Total Harmonic Distortion, THD) misura il rapporto tra le ampiezze delle linee spettrali indesiderate causate dalla distorsione e quella del segnale utile (nota 4); normalmente è espressa in percentuale con la seguente formula:
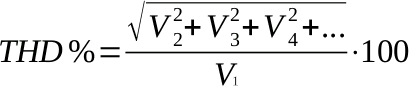
Dove:
Questa misura è tipicamente usata per valutare la qualità degli apparati di riproduzione audio.
In genere è ignorata l'ampiezza della linea spettrale con frequenza 0 (valor medio).
Consideriamo lo spettro seguente; esso mostra l'uscita di un quadripolo il cui ingresso è una sinusoide con frequenza 2 kHz:
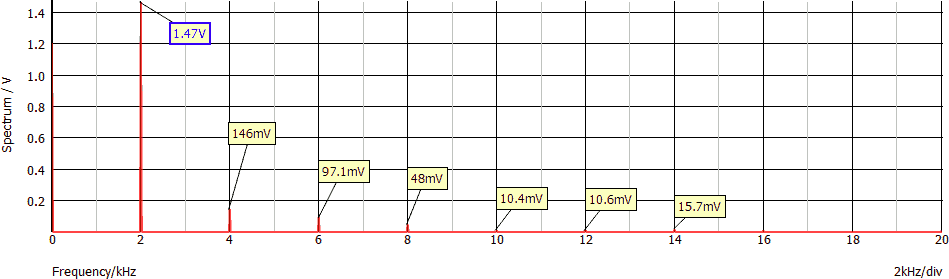
La THD percentuale calcolata con la formula mostrata è circa THD = 12,4%
Questo valore è decisamente elevato in molti campi applicativi. Per esempio, in campo audio viene considerata accettabile una distorsione dell'1%.
L'SFDR (Spurious-Free Dynamic Range) è il rapporto espresso in unità logaritmiche (dBc, dove la "c" indica portante o carrier, termine derivato dalle comunicazioni radio) tra l'ampiezza del segnale utile e quella della più grande tra le linee spettrali indesiderate.
Questa misura è tipicamente usata per valutare la qualità degli apparati radio o dei convertitore AD e DA.
Consideriamo lo stesso spettro già esaminato nel paragrafo precedente, di seguito ridisegnato in unità logaritmiche:
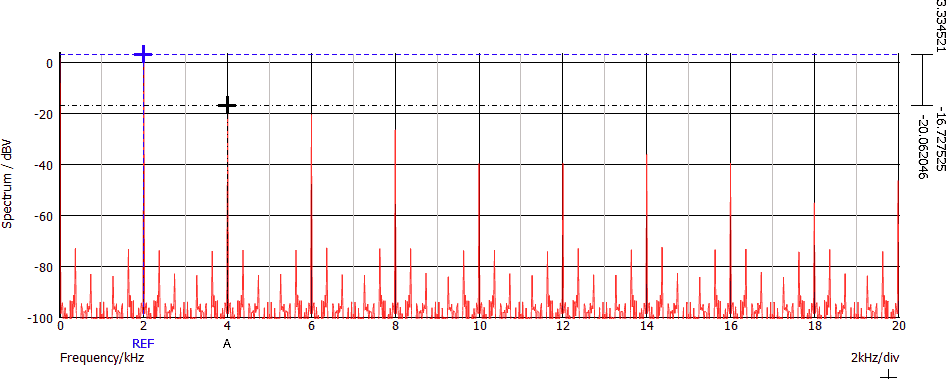
Dal grafico si legge immediatamente che SFDR = 20,1 dBc. A tale risultato si poteva giungere facilmente anche partendo dallo spettro in unità lineari, applicando le proprietà dei logaritmi.
Tra THD e SFDR non esiste alcuna relazione numerica anche se descrivono
entrambe distorsioni non lineari.
Nei circuiti reali distorsione e rumore sono sempre presenti contemporaneamente e quindi potrebbe essere utile esprimere questi difetti con un solo numero. Anche in questo caso esistono numerose misure, spesso complesse e specialistiche; di seguito qualche esempio:
Anche i segnali digitali possono essere distorti da un quadripolo. Per esempio il seguente grafico mostra in blu l'ingresso di una linea di trasmissione ed in rosso l'uscita.
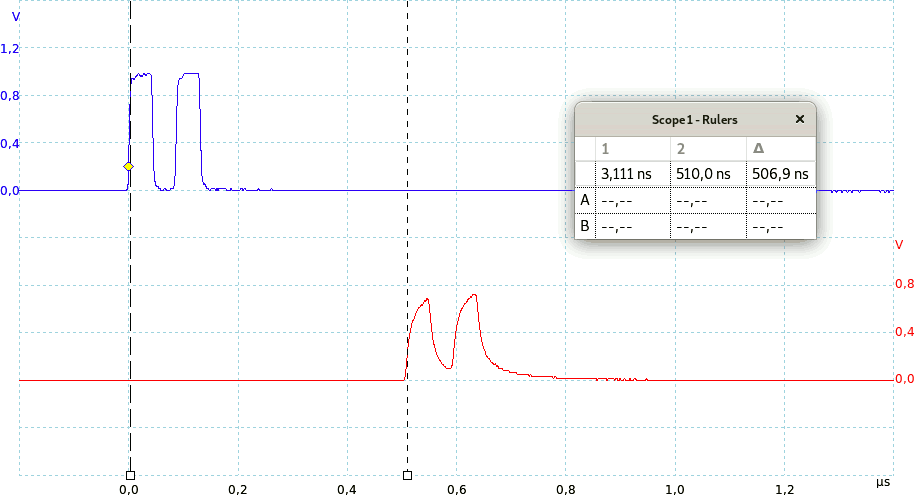
La distorsione è causata dal comportamento non ideale di una linea di trasmissione: infatti un'onda quadra è la somma di sinusoidi con varie frequenza che:
Si può dimostrare che sono invece trascurabili le distorsioni da non linearità.
Pur essendo il segnale di uscita piuttosto distorto, rimangono in questo caso chiaramente riconoscibili i valori alti e bassi. Questo comportamento è tipico dei segnali digitali: distorsioni non troppo grandi sono ininfluenti o quasi.
Se la distorsione fosse invece più ampia di quanto mostrato, un bit potrebbe cambiare valore: è intuitivo immaginare che, maggiore è la distorsione, maggiore sarà la probabilità di avere bit errati. Il tasso di errori in genere viene indicato come BER (Bit Error Rate), definito come rapporto tra il numero di bit errati ed il numero totale di bit. Valori ragionevoli di BER vanno da 10-3 (telefonia di vecchio tipo) a 10-12 (Ethernet).
Pagina creata nell'ottobre 2021
Ultima modifica: 22 gennaio 2026
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)