Un filtro è un quadripolo che permette al segnale sinusoidale applicato in ingresso di arrivare all'uscita solo se la sua frequenza è compresa in un determinato intervallo. Tale intervallo di frequenze viene indicato con il termine di banda passante del filtro oppure, semplicemente, banda (B). La o le frequenze che costituiscono i confini della banda sono indicate come frequenze di taglio (fT).
Se il segnale non è sinusoidale, possiamo scomporlo nelle sue componenti spettrali, alcune delle quali saranno presenti in uscita al filtro ed altre no.
Ovviamente l'immagine di apertura, relativa ad un filtro dell'olio usato nei motori endotermici, non ha nulla a che fare con il contenuto di questa pagina.
I filtri possono essere classificati come:
I simboli spesso utilizzati sono i seguenti, dal significato piuttosto ovvio.
Per descrivere questo comportamento spesso si ricorre al concetto di guadagno:
Un filtro si dice passivo se contiene solo elementi passivi, in genere resistori, induttori e condensatori. In alcuni casi sono presenti anche altri componenti come cristalli di quarzo e trasformatori. Si noti che il segnale di uscita di un filtro passivo deve necessariamente avere una potenza minore o uguale alla potenza del segnale di ingresso: mancano infatti generatori interni al filtro. Il guadagno di potenza è quindi minore di 1 (oppure minore di 0 dB)
Un filtro si dice ideale se il guadagno è costante all'interno della banda e nullo all'esterno.
Fino a non molti anni fa lungo il doppino telefonico viaggiavano contemporaneamente due segnali:
I due segnali si disturbano a vicenda:
La soluzione è stata utilizzare:
Il genere questi filtri erano costruiti in un solo contenitore con un ingresso e due uscite. Spesso sono indicati anche con il termine splitter ADSL (cioè separatori).
Un segnale musicale contiene molte frequenze. Un altoparlante in genere è in grado di riprodurre con fedeltà solo un certo intervallo di frequenze:
Un filtro di cross-over viene inserito tra un amplificatore e un altoparlante per permettere il passaggio delle sole frequenze che un altoparlante può efficacemente riprodurre. In genere tali filtri hanno un ingresso e più uscite, una per ciascun tipo di altoparlante.
Tutti i segnali radiofonici in modulazione di frequenza arrivano contemporaneamente all'antenna ricevente. Ciascun canale radio occupa una banda di circa 250 kHz, scelta in un intervallo tra 87.5 e 108 MHz. Un sintonizzatore radio FM contiene un filtro bassa banda con banda pari a 250 kHz che permette di ascoltare uno solo tra tutti i canali ricevuti (nota 7).
Se il segnale in ingresso ad un convertitore AD non rispetta il teorema del campionamento, in uscita sono presenti linee spettrali non presenti in ingresso. La soluzione universalmente adottata è quella di anteporre al campionatore un filtro passa basso che impedisce il passaggio di frequenze superiori alla metà della frequenza di campionamento: si preferisce infatti digitalizzare, eventualmente, solo una parte del segnale piuttosto che avere uno spettro in cui è impossibile distinguere linee spettrali reali da linee spettrali causate dall'aliasing.
Un filtro reale può essere descritto graficamente dalla sua risposta in frequenza; essa rappresenta il modulo del guadagno (in decibel) in funzione della frequenza su scala logaritmica (nota 3). Matematicamente un filtro è descritto dalla sua funzione di trasferimento, argomento che può essere classificato come avanzato.
Il grafico seguente mostra un esempio con la risposta in frequenza di un filtro passa alto reale:
Leggiamo il grafico:
L'ingresso del filtro descritto dalla risposta in frequenza sopra riportata è una sinusoide con frequenza 100 Hz e ampiezza VIN = 10 V. Calcoliamo il segnale di uscita.
Nell'ipotesi di circuito lineare sappiamo che l'uscita è una sinusoide con frequenza 100 Hz.
Dal grafico leggiamo che il guadagno di tensione a 100 Hz è circa -40 dB, cioè 10(-40/20) = 0,01. L'ampiezza della sinusoide in uscita è quindi circa VOUT = 10 · 0,01 = 0,1 V.
Lo stesso risultato lo si poteva ottenere, più comodamente, usando nei calcoli le unità logaritmiche (nota 4):
Ovviamente -20 dBV = 0,1 V
Lo stesso grafico (nota 5) è utilizzabile anche per le potenze.
Se il segnale in ingresso ha frequenza 1 kHz e potenza 10 dBm, il guadagno vale circa -20 dB e quindi la potenza di uscita è circa -10 dBm.
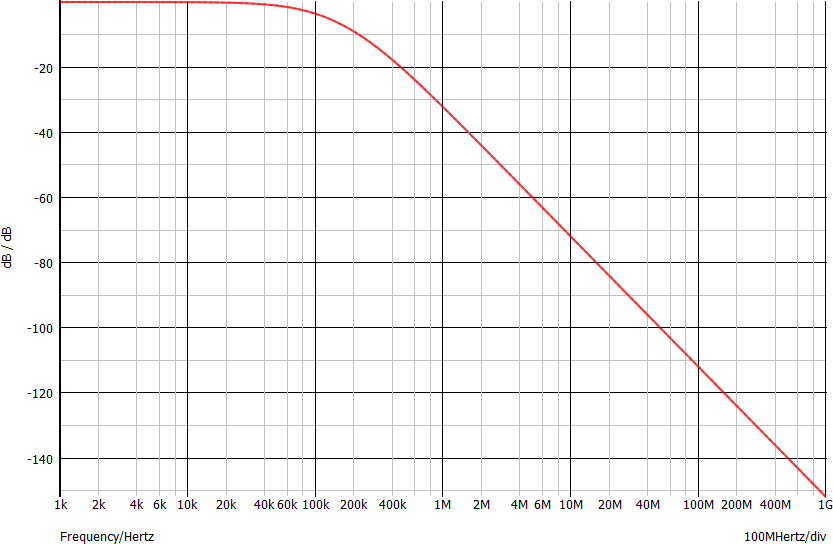
Consideriamo la seguente risposta in frequenza di un filtro passa basso adattato. Il guadagno è pari a circa -6 dB (nota 6) fino a 100 MHz, poi decresce.
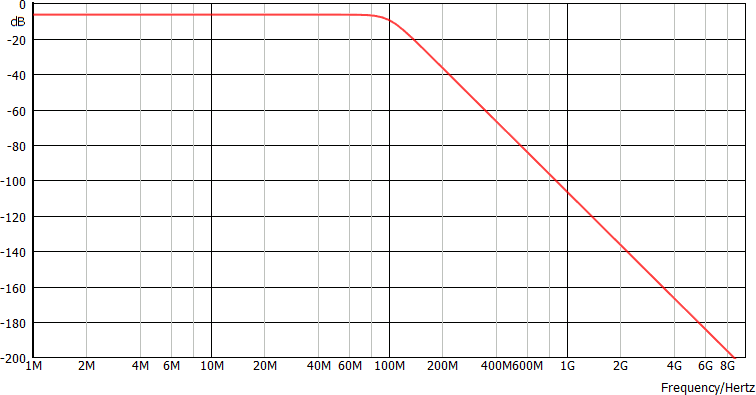
Q1 - L'ingresso è una sinusoide con frequenza 10 MHz e ampiezza 10 dBV. Determinare l'uscita.
Il guadagno a 10 MHz è circa -6 dB. L'uscita è una sinusoide con frequenza 10 MHZ ed ampiezza VOUT = 10 dBV - 6 dB = 4 dBV
Q2 - L'ingresso è una sinusoide con frequenza 1 GHz e ampiezza 0 dBV. Determinare l'uscita.
Il guadagno alla frequenza di 1 GHz è circa -106 dB. L'uscita è una sinusoide con frequenza 1 GHZ ed ampiezza VOUT = 0 dBV - 106 dB = -106 dBV circa
Q3 - L'ingresso è una sinusoide con frequenza 100 MHz e ampiezza 10 V. Determinare l'uscita.
Innanzitutto: VIN = 20 log(10) = 20 dBV. Il guadagno a 100 MHz è circa -9 dB. L'uscita è una sinusoide con frequenza 100 MHZ ed ampiezza VOUT = 20 dBV - 9 dB = 11 dBV circa (3.55 V circa)
(Strada alternativa alla precedente, meno "elegante") Il guadagno di tensione a 100 MHz è pari a circa 10(-9/20) = 0,35, la tensione di uscita è quindi VOUT = 10 · 0.35 = 3,5 V (10.9 dBV circa)
Q4 - L'ingresso è una sinusoide con frequenza 100 MHz e potenza 10 dBm. Determinare l'uscita.
Il guadagno a 100 MHz è circa -9 dB. L'uscita è una sinusoide con frequenza 100 MHZ ed potenza POUT = 10 dBm - 9 dB = 1 dBm circa
Q5 - L'ingresso è una sinusoide con frequenza 100 MHz e potenza 3 mW. Determinare l'uscita.
Innanzitutto: PIN = 10 log(3) = 4,8 dBm. Il guadagno a 100 MHz è circa -9 dB. L'uscita è una sinusoide con frequenza 100 MHZ ed potenza POUT = 4.8 dBm - 9 dB = -4,2 dBm circa (0,38 mW circa)
(Strada alternativa alla precedente, meno "elegante") Il guadagno di potenza a 100 MHz è pari a circa 10(-9/10) = 0,13, la potenza di uscita è quindi POUT = 3 · 0.13 = 0.39 mW (-4,1 dBm circa)
Q6 - L'ingresso è un'onda quadra con frequenza 100 MHz e ampiezza 1 V. Determinare l'uscita.
La risposta è qui complessa, in quanto l'uscita non è un'onda quadra. Possiamo scomporre l'ingresso in una somma di infinite sinusoidi con frequenza 100 MHz, 300 MHz, 500 MHz... e considerare singolarmente il loro contributo, secondo il principio di sovrapposizione degli effetti. Si veda per una soluzione tramite simulazione, l'attività 7.
[Definizione avanzata] Matematicamente viene definito ordine di un filtro (passa alto o passa basso) il numero di poli presenti nella funzione di trasferimento (nota 1).
Graficamente più è elevato l'ordine di un filtro, più è elevata la pendenza dei tratti inclinati della diagramma di Bode, avvicinandosi a quello che è il comportamento di un filtro ideale.
In particolare:
A titolo di esempio si riporta il grafico della funzione di trasferimento reale di un filtro passa basso del primo ordine (rosso), del secondo ordine (blu) e del quarto ordine (verde) con frequenza di taglio pari ad 1 Hz.
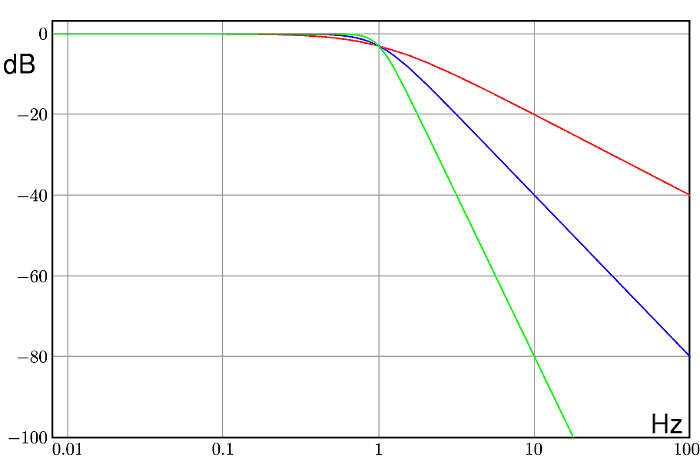
Leggendo il grafico si vede che:
Disegnare la funzione di trasferimento (asintotica) di un filtro con le seguenti caratteristiche:
Per disegnare manualmente la funzione di trasferimento asintotica può essere utile seguire le seguenti indicazioni:
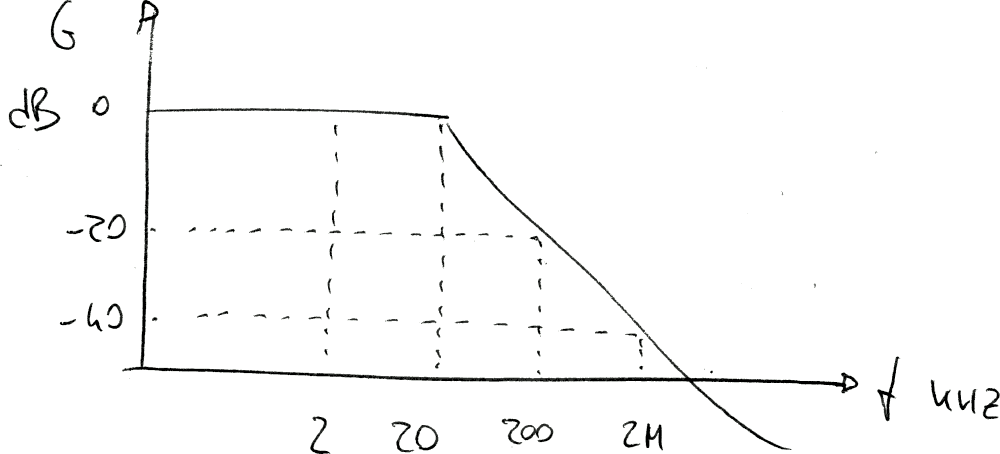
Nella funzione di trasferimento reale il passaggio tre le due rette è più "morbido" ed in corrispondenza della frequenza di taglio la linea reale differisce da quella asintotica di 3 dB.
Disegnare la funzione di trasferimento (asintotica) di un filtro con le seguenti caratteristiche:
Il procedimento è analogo al precedente, ma trattandosi di un filtro del secondo ordine, conviene indicare il guadagno a passi di 40 dB.
Inoltre il tratto orizzontale deve essere disegnato nella parte destra del grafico. Il tratto inclinato non deve passare necessariamente per l'origine.
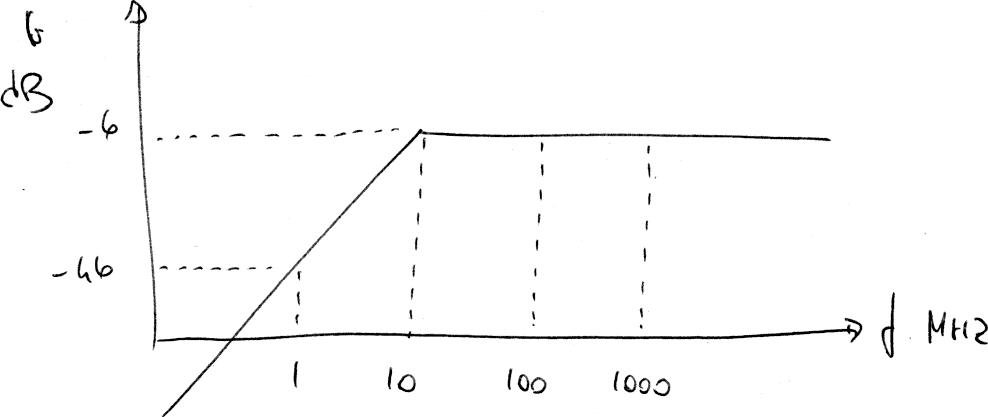
Nella funzione di trasferimento reale il passaggio tre le due rette è più "morbido" ed in corrispondenza della frequenza di taglio la linea reale differisce da quella asintotica di 3 dB.
Disegnare la funzione di trasferimento di un filtro con le seguenti caratteristiche:
Il procedimento è analogo ai precedenti, ma trattandosi di un filtro del quarto ordine, conviene indicare il guadagno a passi di 80 dB.
Data la seguente funzione di trasferimento di un filtro adattato:
Determinare:
I filtri possono essere realizzati in differenti tipologie a secondo degli aspetti che più interessano una determinata applicazione. Tre tipi (tra i tanti) ampiamente utilizzati sono descritti brevemente in seguito.
Questi filtri presentano un guadagno in banda passante costante (in termini tecnici: massimamente piatto). Il diagramma di Bode di tale tipologia di filtro, per vari ordini, è quello dell'esempio sopra riportato: si osservi come per le frequenze basse il guadagno sia effettivamente "piatto".
In questo tipo di filtro la frequenza di taglio fT è definita come quella frequenza in cui il guadagno è inferiore di 3 dB al valore massimo assunto in banda passante, indipendentemente dall'ordine. Quindi i tre filtri dei quali è disegnata la risposta in frequenza hanno la stessa banda (pari a 1 Hz)
Questi filtri presentano un passaggio brusco tra il guadagno in banda passante e quello in banda attenuata, a scapito della "piattezza" della risposta in banda passante. Uno dei parametri di progetto è la fascia massima di oscillazione del guadagno in banda passante, identificata dalla linea tratteggiata in figura (3 dB nell'esempio).
La frequenza di taglio per questi filtri è definita come la frequenza alla quale il guadagno esce definitivamente dalla fascia di oscillazione (in figura: 1 Hz)
Il grafico seguente mostra il confronto tra la risposta in frequenza di un filtro di Chebychev (in rosso) ed uno di Butterworth (in verde). I due filtri hanno la stessa banda (1 Hz) e lo stesso ordine (quarto). Si osservi che nel tratto a destra nel grafico le due linee sono parallele e con pendenza pari a -80 dB/decade. In corrispondenza della frequenza di taglio invece la pendenza appare molto diversa.
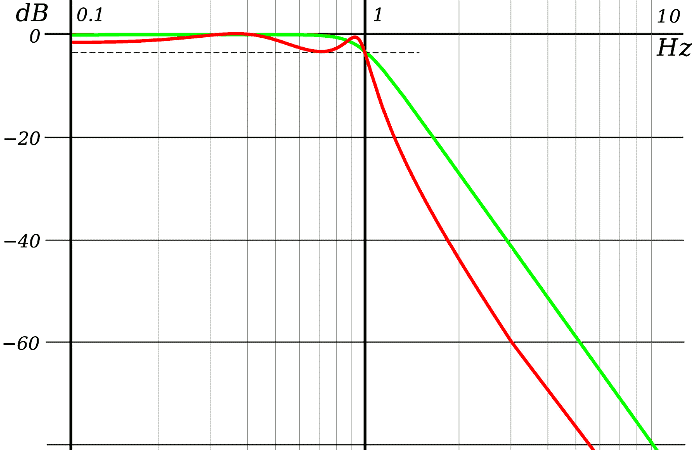
Questi filtri assomigliano nel modulo a quelli di Butterworth, ma presentano un andamento della fase più lineare. Non sono qui trattati.
Pagina creata nel dicembre 2012
Ultima modifica: 10 novembre 2024
Appunti scolastici - Versione 0.1029 - Gennaio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)
