
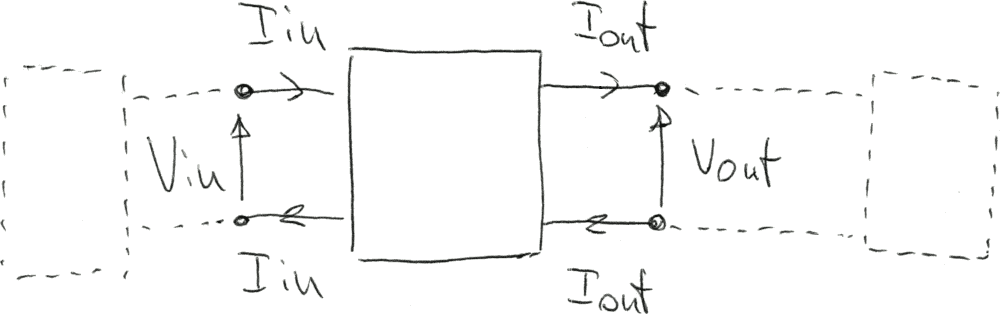
Un quadripolo è un circuito dotato di due morsetti per il segnale di ingresso e due morsetti per il segnale di uscita.
Normalmente è disegnato con un rettangolo vuoto, come nella figura di apertura; sono messe in evidenza le tensioni e le correnti di ingresso (Vin e Iin, a sinistra) e di uscita (Vout e Iout, a destra; nota 6). Esse dipendono sia dalle caratteristiche del quadripolo che dai circuiti collegati all'ingresso e all'uscita, in figura tratteggiati (nota 1).
In genere non sono disegnati eventuali generatori che alimentano il quadripolo, aspetto tipico dei quadripoli attivi.
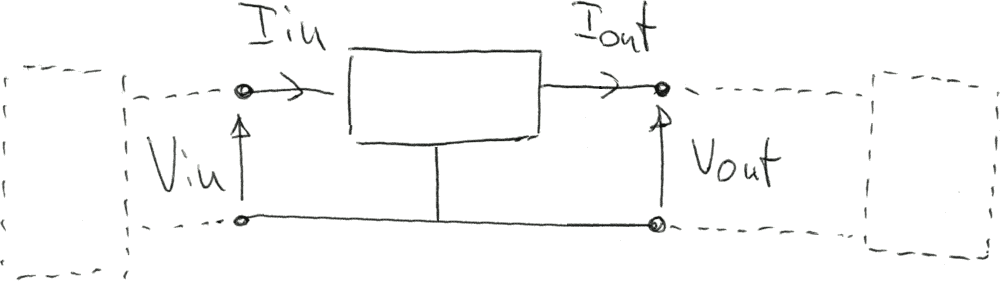
Un caso particolare è il tripolo: in esso i due terminali di ingresso ed uscita in basso sono collegati tra di loro e, in genere, alla massa dell'intero circuito.
Esempi di quadripoli nell'ambito delle telecomunicazioni sono i filtri passivi, gli amplificatori, le linee di trasmissione.
La descrizione matematica di un quadripolo costituito solo da elementi lineari (resistori, generatori dipendenti, condensatori, induttori, trasformatori...) è piuttosto complessa e viene fatta, per esempio, attraverso l'uso di matrici. Ancora più complessa la descrizione di quadripoli non lineari, contenenti anche diodi, transistor. MOS...
Di seguito verrà fatta una descrizione semplificata, limitatamente alle tipiche applicazioni nel campo delle telecomunicazioni.
Si definisce (nota 5) guadagno (G, gain) il rapporto tra una grandezza elettrica di uscita e la corrispondente di ingresso. Esso è adimensionale, cioè un numero puro, senza unità di misura (nota 3).
Il guadagno di tensione GV è definito come:
GV = Vout / Vin
Normalmente si utilizza il valore efficace della tensione, per definizione sempre positivo; di conseguenza anche il guadagno è positivo (nota 2).
Se il modulo del guadagno di tensione è maggiore di uno, evidentemente la tensione di uscita è, in modulo, maggiore di quella di ingresso.
Analogamente il guadagno di corrente GA è definito come:
GA = Iout / Iin
Il guadagno di corrente è meno utilizzato nell'ambito delle telecomunicazioni e probabilmente non verrà più citato in questi appunti.
Il guadagno di potenza è definito come:
GP = Pout / Pin = (Vout · Iout ) / (Vin · Iin)
La potenza da utilizzare è quella media; il guadagno di potenza è sempre positivo. Se il guadagno di potenza è maggiore di uno, evidentemente la potenza di uscita è maggiore di quella di ingresso. Solo i quadripoli attivi possono avere un guadagno di potenza maggiore di uno.
In molti quadripoli i guadagni dipendono, oltre che dalle caratteristiche del quadripolo, sia dal circuito collegato in ingresso, sia dal circuito collegato in uscita, complicando notevolmente i calcoli teorici.
Viene definita (nota 5) attenuazione di tensione (αV, α è la lettere greca alfa) il reciproco del guadagno di tensione:
αV = Vin / Vout = 1 / GV
Analogamente possiamo definire l'attenuazione di potenza:
αP = Pin / Pout = 1 / GP
Si definisce (nota 5) impedenza (o resistenza) di ingresso di un quadripolo (Zin) il rapporto tra tensione di ingresso e corrente di ingresso:
Zin = Vin / Iin
L'unità di misura è l'ohm.
Si definisce (nota 5) impedenza (o resistenza) di uscita (Zout) di un quadripolo il rapporto tra tensione di uscita e corrente di uscita:
Zout = Vout / Iout
L'unità di misura è l'ohm.
In molti quadripoli le impedenze dipendono sia dal circuito collegato in ingresso, sia dal circuito collegato in uscita, complicando notevolmente i calcoli teorici.
Un apparato di telecomunicazioni ben progettato cerca di rispettare le seguenti caratteristiche. Si tratta di obbiettivi che, con risultati più o meno ottimali, sono raggiunti dagli apparati commerciali. In queste pagine non sono descritte tecniche per ottenere questi risultati...
Obbiettivo 1: le impedenze di ingresso ed uscita:
Obbiettivo 2: Zin dovrebbe essere uguale a Zout. In questo caso si dice che il quadripolo è simmetrico e l'impedenza è indicata come impedenza caratteristica del quadripolo (Z0).
Obbiettivo 3: a seconda delle applicazioni, gli apparati dovrebbero essere progettati per avere un'impedenza caratteristica Z0 di valore standard. Per esempio:
Un quadripolo correttamente progettato ed utilizzato presenta le seguenti grandezze in ingresso ed uscita. Calcolare i guadagni e le impedenze:
GV = 2 / 0,1 = 20
GI = 30 / 1 = 30
GP = (30·10-3 · 2) / (1·10-3 · 0,1) = 600
Zin = 100 / 1 = 100 Ω
Zout = 2 / 0.03 = 67 Ω
In questo esempio, diversamente da quanto avviene in molti apparati reali, le impedenze di ingresso e di uscita sono diverse tra di loro: si tratta quindi di un quadripolo non simmetrico. Inoltre nessuna delle due impedenze assume un valore standard.
Un quadripolo presenta:
Calcolare:
In molti casi un quadripolo è collegato a:
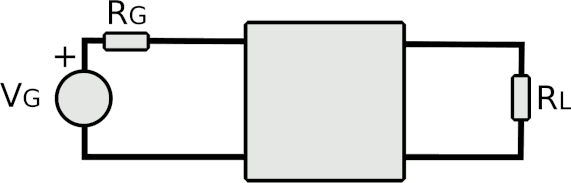
Si può dimostrare che, al fine del miglior funzionamento dell'intero circuito, è necessario che:
Queste sono chiamate condizioni di adattamento e devono essere sempre rispettate nei circuiti ad alta frequenza. Un quadripolo che le rispetta è detto adattato.
In queste condizioni la potenza erogata a RL è quella massima ottenibile (nota 4) e sono assenti distorsioni e "riflessioni" del segnale trasmesso.
L'immagine seguente mostra una situazione piuttosto comune nei sistemi di telecomunicazione: tre quadripoli sono collegati tra di loro in cascata e mettono in comunicazione un generatore (VG con la sua resistenza interna RG) ad un carico, modellizzato da RL.

La rete è adattata se:
In questo caso il guadagno complessivo è pari al prodotto del guadagno dei singoli quadripoli, risultato che semplifica di molto lo studio della rete (nota 7).
G = VL / VG = G1 · G2 · G3
Per rispettare le condizioni di adattamento a volte è necessario inserire adattatori di impedenza, cioè quadripoli non simmetrici che presentano:
Pagina creata nell'agosto 2024
Ultima modifica: 16 settembre 2024
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)