
In questa pagina cerco di spiegare il significato di potenza elettrica in circuiti in cui tensione e corrente sono variabili nel tempo.
La potenza istantanea è, istante per istante, il prodotto di tensione e corrente, esattamente come definito per il caso di tensioni continue.
Nel caso in cui la tensione (o la corrente) è variabile, ovviamente è variabile anche la potenza istantanea. A volte la potenza istantanea è indicata come P(t) per sottolineare il fatto che è una funzione dipendente nel tempo.
La potenza media (o semplicemente potenza, se non vi sono dubbi interpretativi), è la media dei valori istantanei all'interno di un certo intervallo di tempo. Per i segnali periodici la potenza media viene calcolata per un periodo (nota 1).
Se non vi va: saltatelo...
Consideriamo il circuito seguente, formato da un generatore sinusoidale (2 V di picco, frequenza 1 kHz) ed un resistore (12 kΩ).

Troviamo quanto valgono la tensione, la corrente e la potenza (medie ed istantanee). Il calcolo può essere svolto secondo il seguente schema (nota 2):
Qui, nella prima parte, la traccia di soluzione analitica. In attesa di digitalizzazione...
Analizziamo lo stesso circuito dell'esercizio 1 con un simulatore, per esempio SIMetrix/SIMPLIS Elements.
Nel grafico seguente in rosso la tensione ed in blu la corrente. Tali grafici, a meno dei segni, valgono sia per il generatore che per il resistore, essendo contemporaneamente sia in serie che in parallelo.
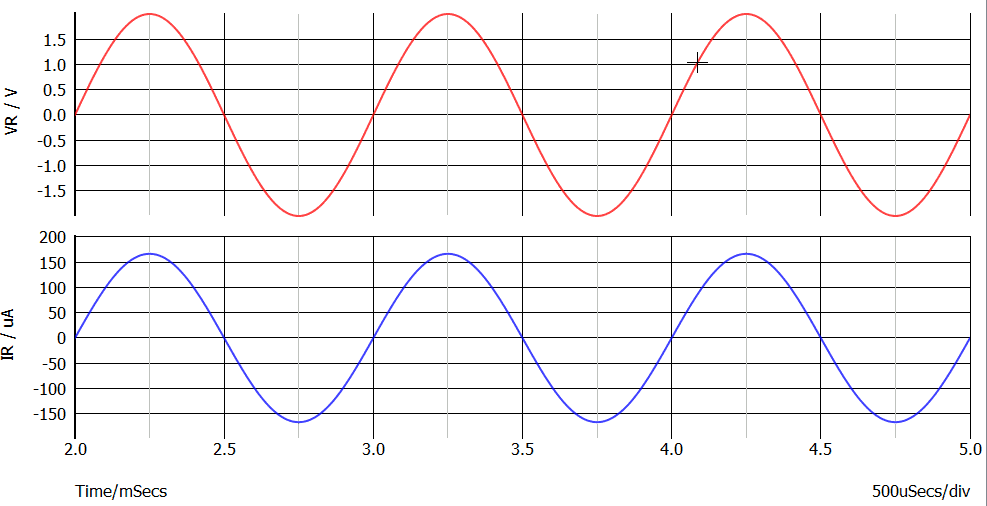
Alcune osservazioni:
Il grafico seguente mostra in verde il grafico della potenza istantanea dissipata dalla resistenza:
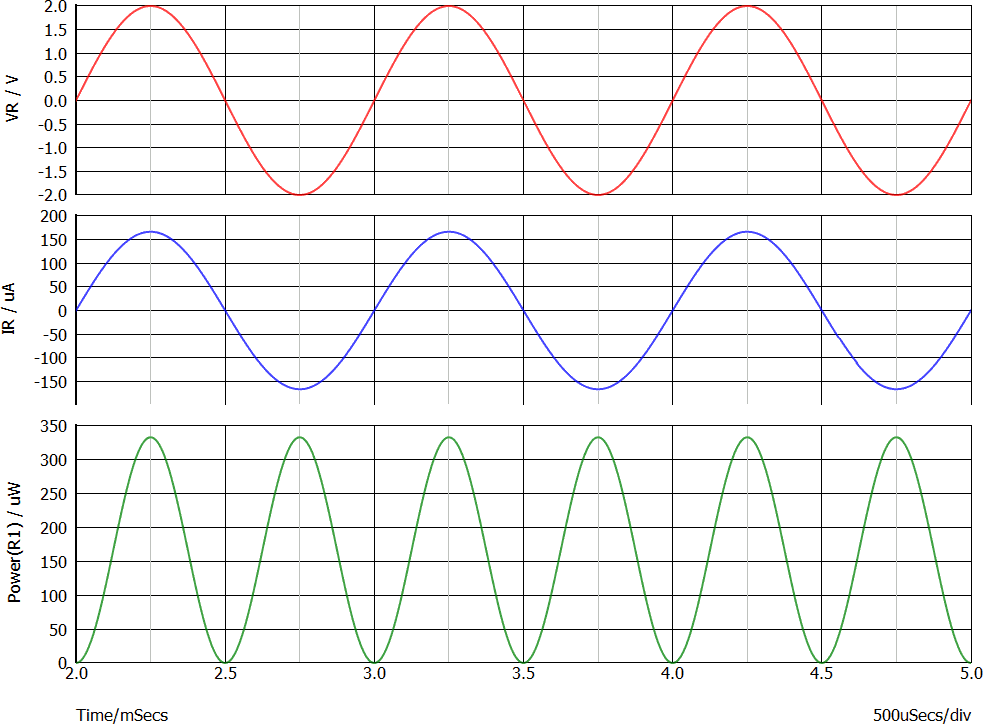
Si tratta di una sinusoide con valor medio diverso da zero che ha le seguenti caratteristiche:
La potenza (media) può essere calcolata anche come prodotto della tensione efficace per la corrente efficace oppure come (VRMS)2 / R, formule valide esclusivamente per i resistori:
W = VRMS · IRMS = (VRMS)2 / R
Se un componente assorbe una potenza (media) maggiore di zero significa che trasforma questa energia in un'altra forma; nel caso dei resistori in calore.
Attenzione: la nomenclatura non aiuta! La potenza media (o semplicemente la potenza) è il prodotto della tensione efficace per la corrente efficace. Per evitare errori, ricordarsi che:Se non vi va: saltatelo...
Consideriamo il circuito seguente, formato da un generatore sinusoidale (2 V di picco, frequenza 1 kHz), un condensatore (10 nF) ed un resistore (10 kΩ).
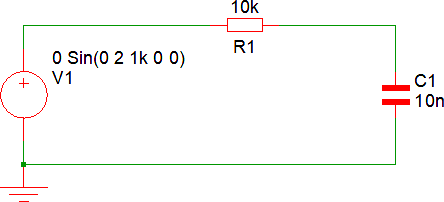
Troviamo quanto valgono le tensioni, la corrente e le potenze (medie ed istantanee). Il calcolo può essere svolto secondo il seguente schema (nota 2):
Qui la traccia di soluzione analitica, in attesa di digitalizzazione...
Analizziamo lo stesso circuito dell'esercizio 3 con un simulatore, per esempio SIMetrix/SIMPLIS Elements.
Analizziamo il condensatore. In rosso la tensione ed in verde la corrente (nota 4).
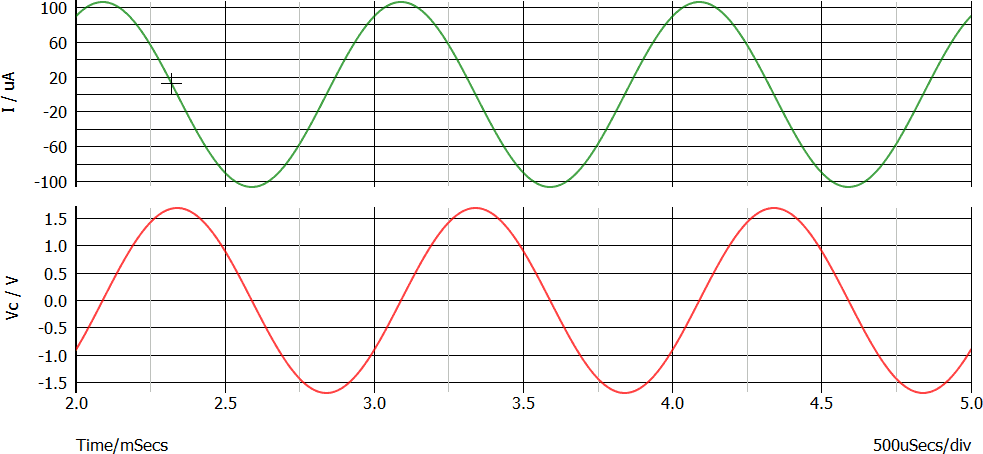
Le due sinusoidi sono tra di loro sfasate di 90°, come qui mostrato in forma analitica oppure come si può misurare con i cursori.
La potenza istantanea è il prodotto, punto per punto, di tensione e corrente. Ovviamente tale prodotto si annulla quando la tensione (oppure la corrente) si annulla. Il grafico è la linea azzurra nel grafico seguente, come ha scoperto per via analitica chi ha svolto il precedente esercizio 3:
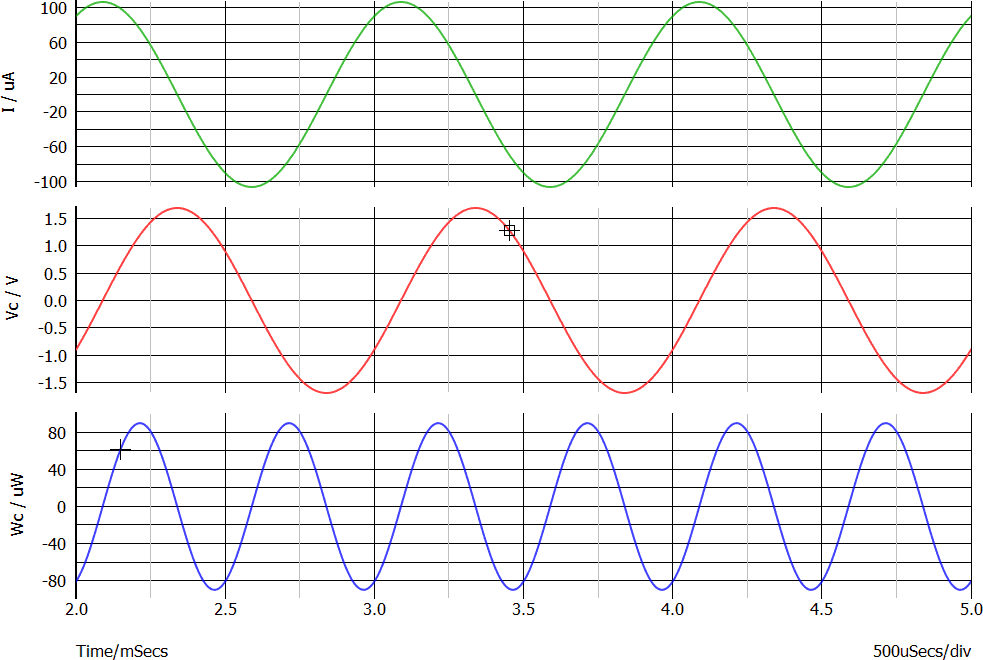
Si tratta di una sinusoide che ha le seguenti caratteristiche:
La potenza (media) dissipata da un condensatore (ideale) è quindi nulla; in altri termini: un condensatore ideale non si riscalda qualunque sia la corrente che lo attraversa e qualunque sia la tensione applicata ai suoi capi.
Possiamo pensare al condensatore come ad un componente che assorbe energia caricandosi quando la potenza è positiva e la restituisce scaricandosi quando la potenza è negativa.
Il seguito il grafico mostra la corrente nel resistore (verde), la tensione ai suoi capi (rosso) e la potenza (blu) (nota 4).
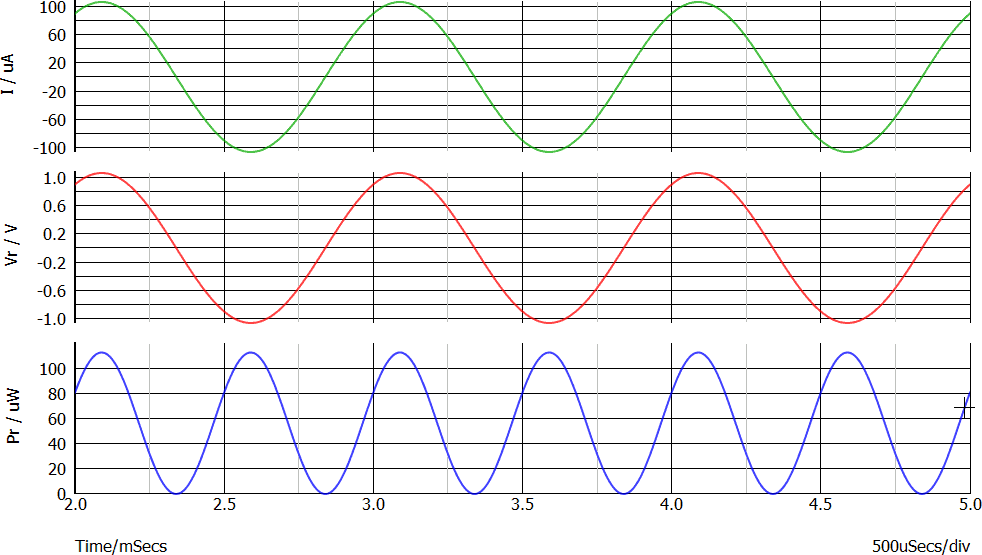
I tre grafici sono analoghi all'esempio 2.
In particolare la potenza istantanea è una sinusoide traslata verticalmente che ha le seguenti caratteristiche:
Il calcolo rigoroso della potenza media è complesso, ma una valutazione intuitiva ci porta a dire che è poco più di 55 µW, cioè la media tra massimo e minimo (la curva è chiaramente simmetrica). il valore corretto può essere "misurato" con il simulatore; in alternativa (nota 3) può essere calcolato come prodotto della tensione efficace (752 mV) moltiplicata per la corrente efficace (75.2 µA): vale circa 56 µW.
Se un componente assorbe una potenza (media) maggiore di zero significa che trasforma questa energia sotto un'altra forma; nel caso dei resistori in calore.
Il seguito il grafico mostra la corrente nel generatore (verde), la tensione ai suoi capi (rosso) e la potenza (blu) (nota 4).
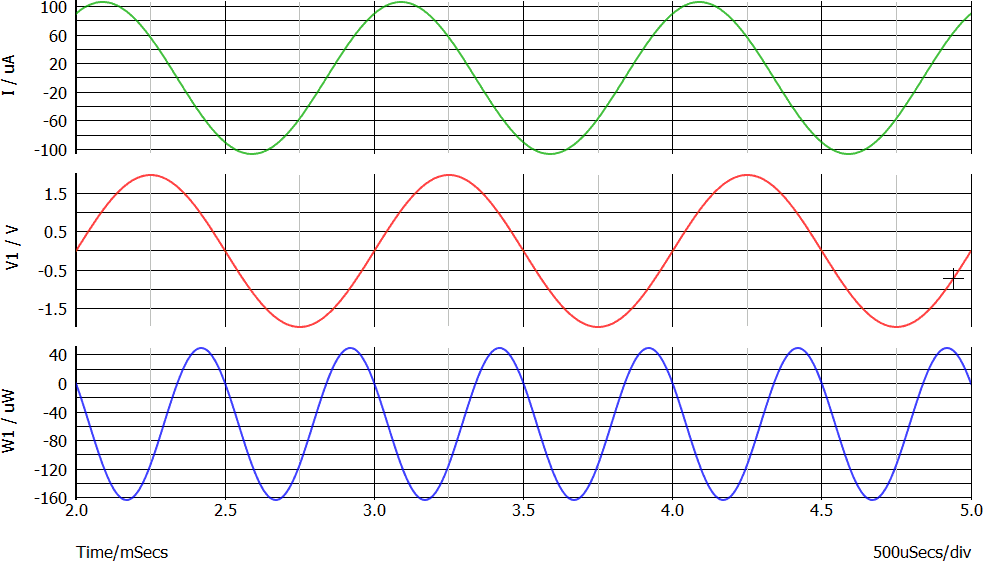
Leggendo il grafico (e con l'aiuto dei cursori, qui non mostrati) possiamo "misurare" i valori di picco ed efficaci e la fase φ tra le due sinusoidi:
Il grafico della potenza istantanea è una sinusoide traslata verticalmente che ha le seguenti caratteristiche:
Questa potenza (media) negativa è quella che il generatore fornisce al circuito; non casualmente coincide in modulo con la somma delle potenze medie dissipate da R e C.
La potenza (media) erogata dal generatore può essere calcolata come prodotto della tensione efficace per la corrente efficace per il coseno dello sfasamento φ tra tensione e corrente:
W = VRMS · IRMS · cos(φ) = 56 µW
Il termine cos(φ) è a volte indicato come fattore di potenza.
Quest'ultima formula è valida per tutti gli elementi lineari e include come casi particolari:
Consideriamo un MOS che pilota in ON/OFF un carico. Il circuito è descritto descritto in questa pagina, ma siamo ora interessati solo a visualizzare la potenza istantanea e media.
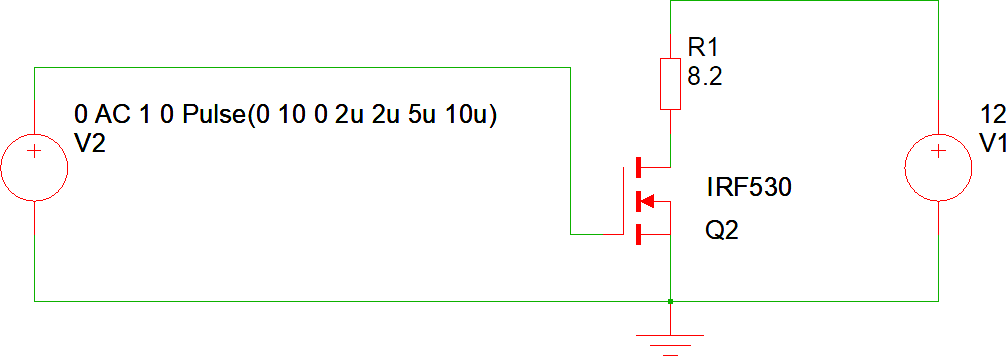
Di seguito il grafico della tensione sul Drain (in rosso) e della corrente di Drain (in verde).
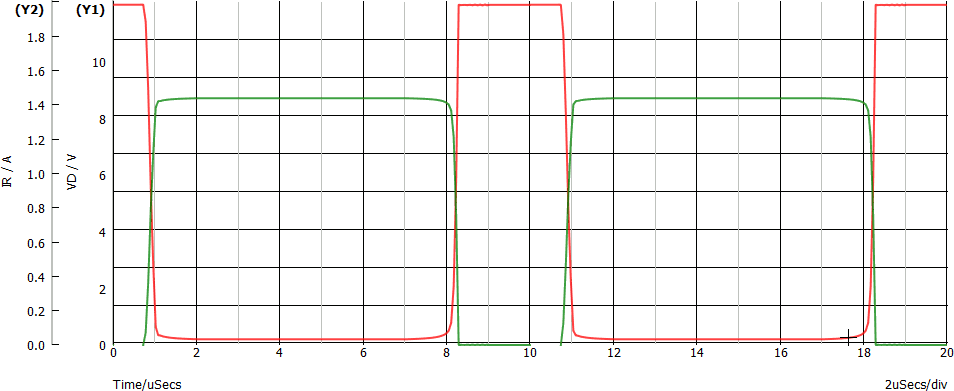
Possiamo individuare tre situazioni ben precise:
Il calcolo della potenza istantanea e della potenza media è ovviamente complesso senza usare il simulatore. Di seguito il grafico con la potenza istantanea:
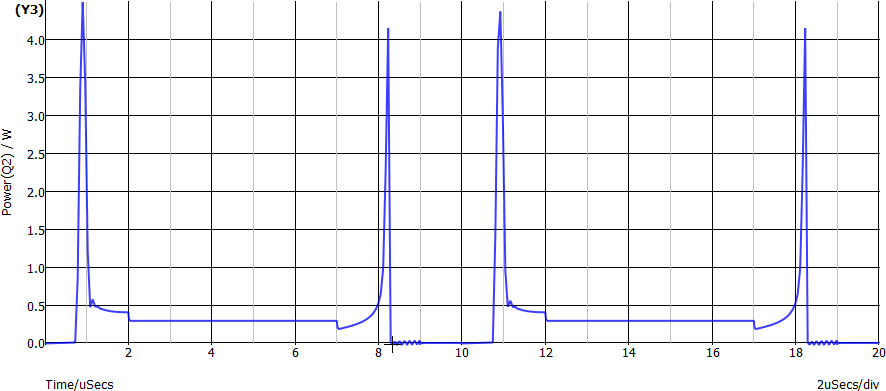
La potenza media non è individuabile senza strumenti specifici. Vale circa 375 mW.
Pagina creata nel settembre 2020
Ultima modifica: 7 gennaio 2023
L'immagine di apertura mostra un agricoltore lucano; non è un fattore di Potenza, ma di Matera.
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)