
Il metodo simbolico è una tecnica che permette di applicare gli stessi strumenti nati per la soluzione dei circuiti in corrente continua anche a quelli in corrente alternata. Per esempio la formula di Ohm, i principi di Kirchhoff oppure la definizione di circuito equivalente di Thévenin rimangono formalmente invariati.
Il metodo è applicabile alle seguenti condizioni:
A queste condizioni (nota 3) si verifica che tutte le tutte le correnti e tutte le tensioni presenti nel circuito sono sinusoidali e con la stessa frequenza.
Come già visto una tensione sinusoidale è rappresentata nel dominio del tempo (ovviamente...) da una sinusoide. Qui sotto un esempio di rappresentazione grafica:
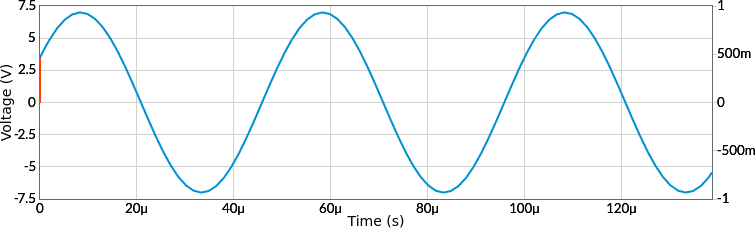
Guardando il grafico, concentriamoci su due soli parametri:
Una sinusoide può essere immaginata come generata dalla rotazione di un vettore in senso positivo (antiorario), a velocità costante e a partire da una certa posizione. Una rappresentazione grafica animata è disponibile all'indirizzo upload.wikimedia.org/.../Unfasor.gif.
Questo vettore rotante viene identificato con il termine fasore.
Nel grafico seguente è rappresenta la stessa sinusoide di apertura attraverso un fasore:
Questa rappresentazione può essere facilmente disegnata a partire dalla sinusoide per via grafica, applicando formule trigonometriche oppure tramite il teorema di Pitagora. Analogamente, dato un fasore possiamo facilmente disegnare la sinusoide corrispondente.
Il disegno del fasore non contiene informazioni sulla forma del segnale, che comunque è sempre sinusoidale, né sulla sua frequenza, che deve essere specificata a parte.
Rispondere, senza passaggi numerici o formule, alle seguenti domande:
In questo paragrafo è mostrato il legame tra tensione e corrente in resistori, condensatori ed induttori.
Partiamo da un dato sperimentale. Il componente in esame è collegato ad un generatore di tensione sinusoidale, curva verde nei tre prossimi grafici. Sullo stesso grafico è disegnata la corrente con una linea tratteggiata azzurra. In questo momento non siamo interessati alla frequenza, uguale per entrambi i segnali, alla forma, che comunque sappiamo essere sempre sinusoidale, e neppure all'ampiezza.
In un resistore tensione e corrente sono in fase tra di loro, cioè entrambe passano per l'asse orizzontale nello stesso istante:
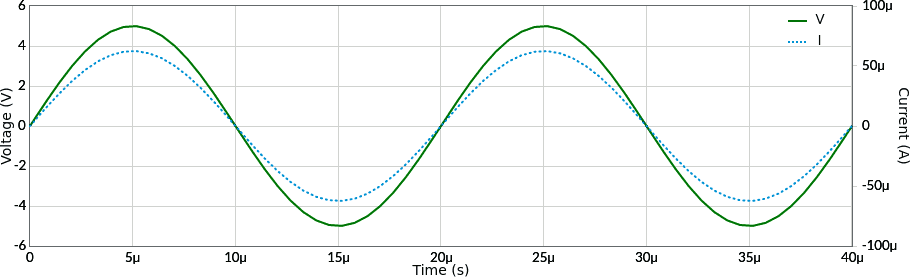
In un induttore la corrente è in ritardo di 90° rispetto alla tensione, cioè la curva della corrente attraversa l'asse orizzontale dopo la curva della tensione. Questo ritardo è per ad 1/4 del periodo oppure, parlando in termini di angoli, arriva 90° gradi dopo (nota 2):
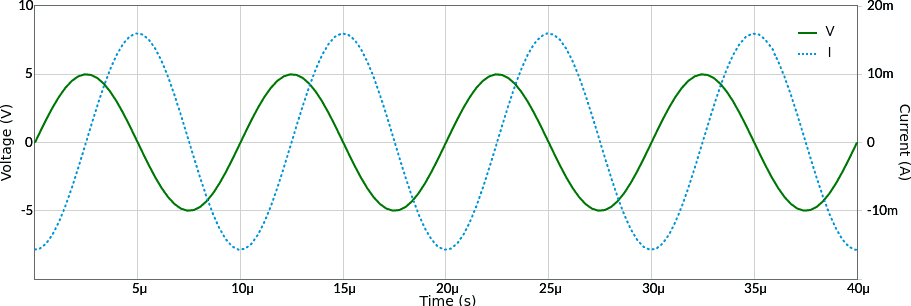
In un condensatore la corrente è in anticipo di 90° rispetto alla tensione:
Possiamo rappresentare tensione e corrente con due fasori. Per esempio, nel caso del condensatore, la tensione ha fase zero e la corrente fase +90°:
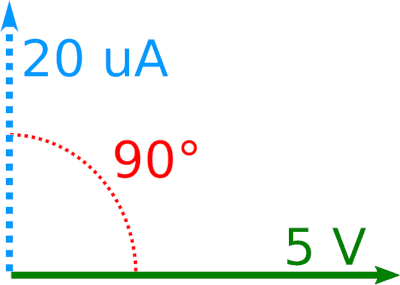
Disegnare i fasori per tensione e corrente nel caso dell'induttore e del resistore
Per utilizzare nella risoluzione dei circuiti AC gli stessi strumenti usati per la risoluzione dei circuiti DC occorre trasformare:
La scelta è quella di utilizzare i numeri complessi per rappresentare sia l'impedenza dei componenti che i segnali.
Una tensione si rappresenta attraverso un numero complesso, osservando l'analogia tra la rappresentazione grafica di un fasore e quella di un numero complesso:
La sinusoide disegnata all'inizio di questa pagina nel dominio del tempo si esprime quindi con il numero complesso:
![]()
Le correnti si rappresentano in modo assolutamente analogo alle tensioni.
L'equivalente della resistenza in regime sinusoidale è detta impedenza. Essa può essere calcolata con la legge di Ohm, dopo aver rappresentato tensione e corrente con un numero complesso.
Per esempio, consideriamo il condensatore a cui si riferisce il grafico sinusoidale appena mostrato ed il corrispondente fasore. Calcoliamo l'impedenza:
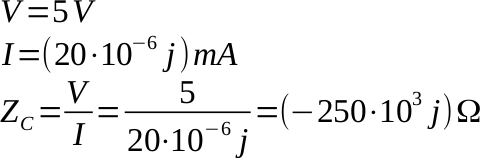
Due osservazioni:
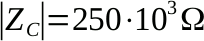
Più in generale, le impedenze di condensatori, induttori e resistori sono espresse con le seguenti formule:
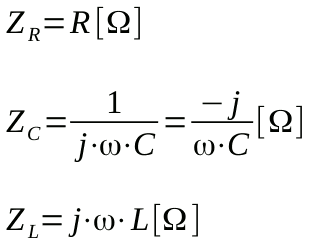
Disegnando tali impedenze come vettori si osserva che:
L'uso di numeri complessi per rappresentare le impedenze rende possibile applicare le formule già viste per i resistori in serie e in parallelo.
Trovare l'impedenza complessiva dei tre seguenti componenti in serie alla frequenza di 20 kHz
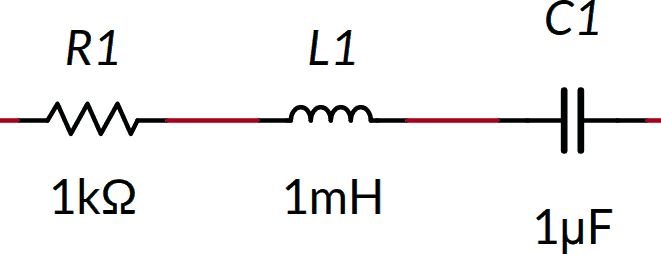
Occorre trovare le impedenze dei tre componenti, usando le formule proposte, e sommarle:
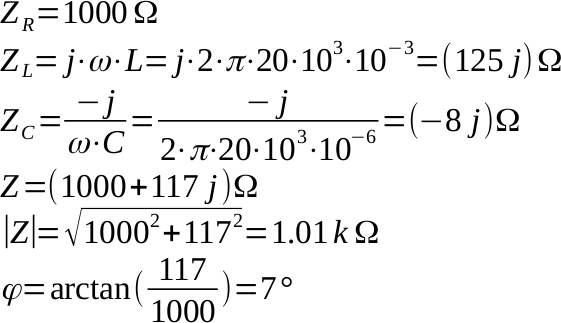
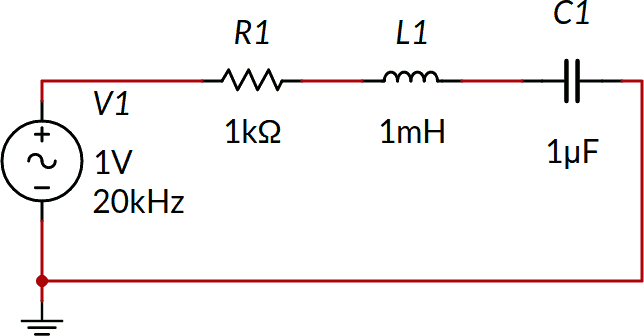
Trovare la corrente nel seguente circuito:
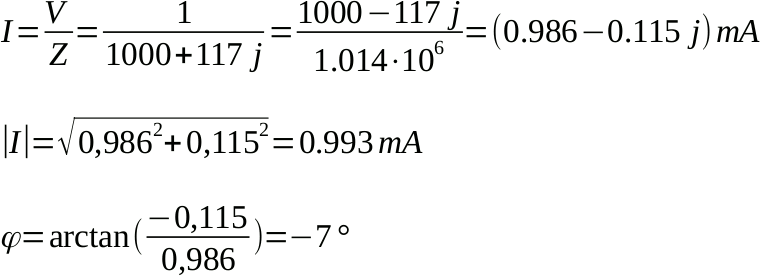
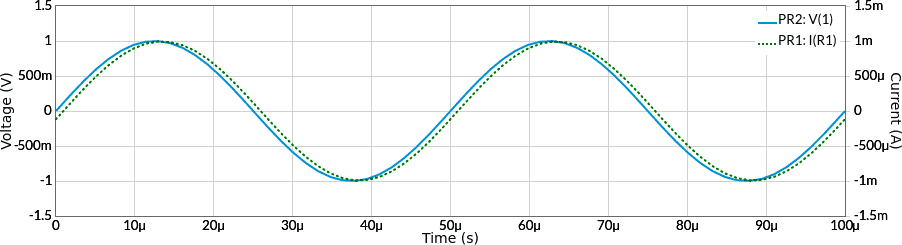
La corrente è quindi sinusoidale (non servono calcoli per saperlo!), con frequenza 20 kHz (non servono calcoli per saperlo!), leggermente in ritardo rispetto alla tensione (fase negativa), con ampiezza di poco meno di 1 mA. Possiamo rappresentarla insieme alla tensione del generatore sia nel dominio del tempo che come fasore:
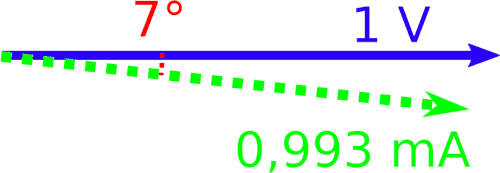
Con gli stessi dati degli esempi precedenti, trovare l'impedenza dei tre componenti RLC quando la frequenza è 200 kHz. Trovare la corrente nel circuito
Trovare l'impedenza dei due componenti RC in parallelo. Trovare la corrente erogata dal generatore.
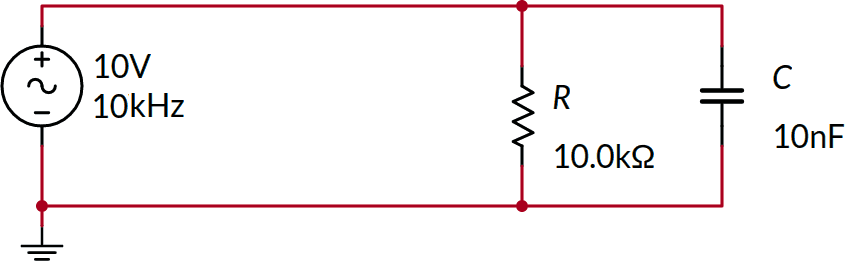
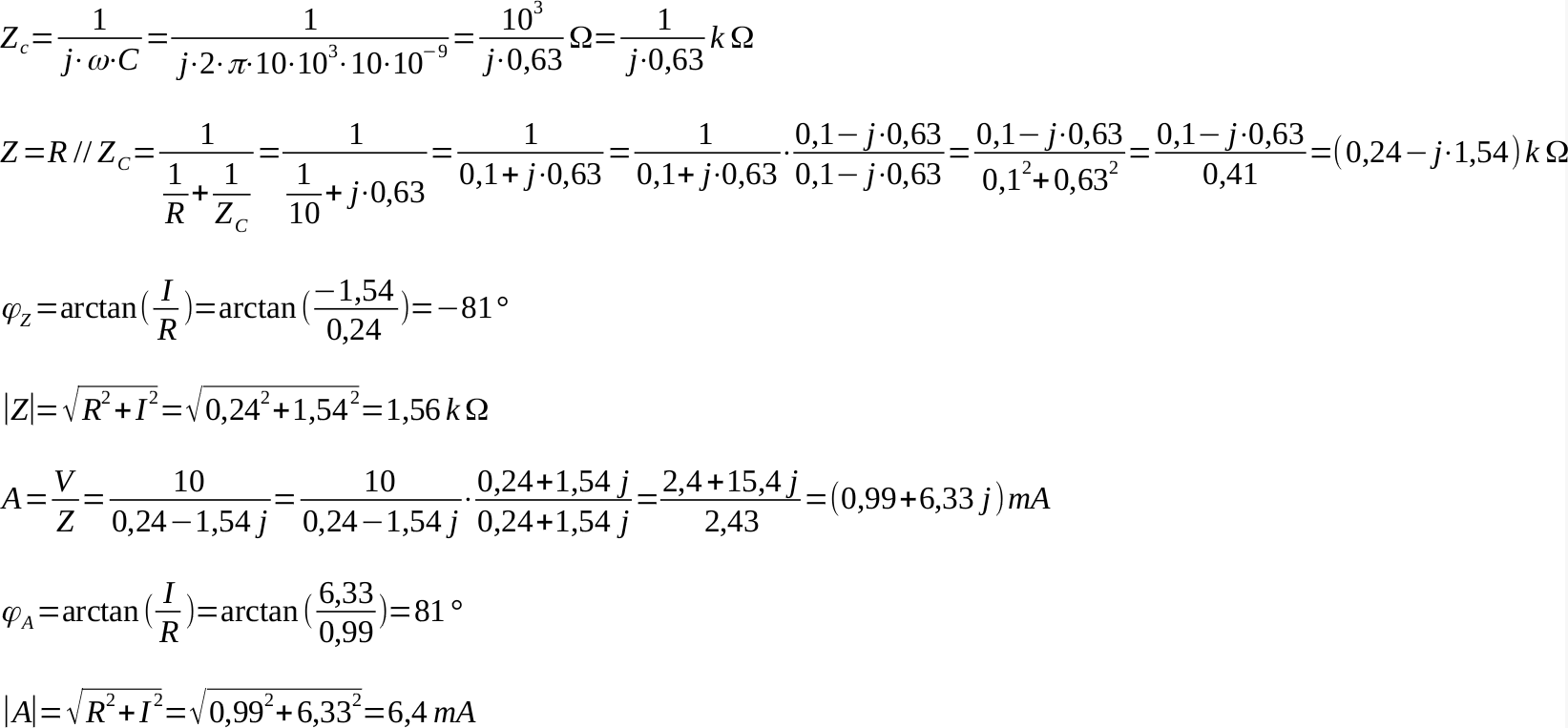
I grafici seguenti sono ottenuti con un simulatore confermano i risultati precedenti:
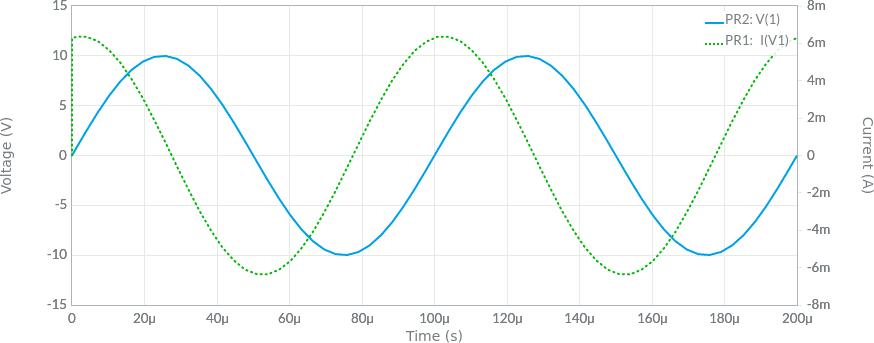
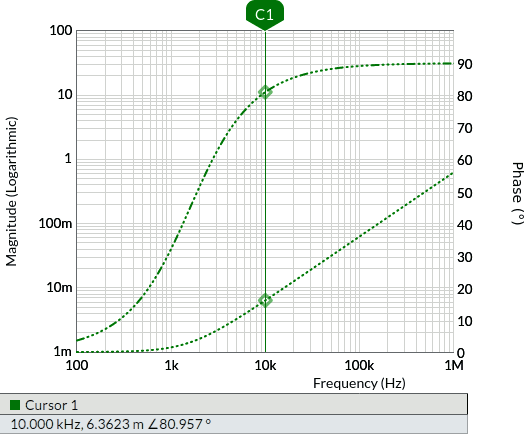
Con gli stessi dati degli esempi precedenti, trovare l'impedenza dei tre componenti RLC in parallelo. Trovare la corrente erogata dal generatore
Quanto vale l'impedenza del seguente circuito? Quanto vale la corrente?
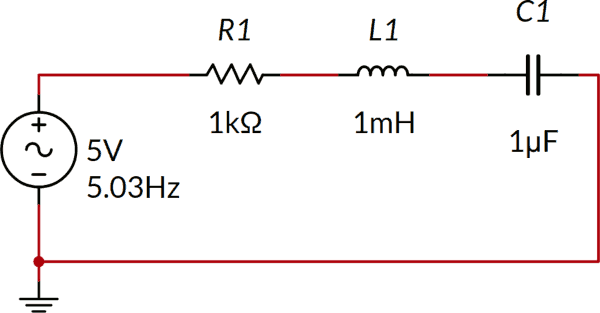
Calcoliamo le impedenze e la corrente:
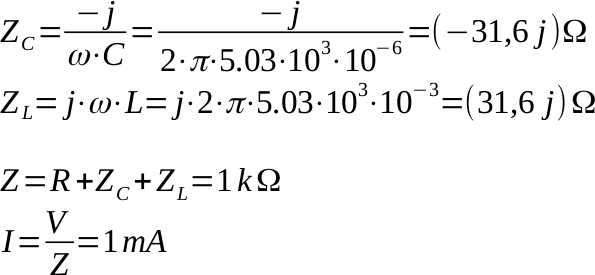
La condizione per cui si annulla la parte immaginaria dell'impedenza (o della corrente) è chiamata condizione di risonanza.
Data di creazione di questa pagina: dicembre 2012
Ultima modifica: 25 maggio 2020
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)