Numeri complessi

Home → Tutorial → Appunti scolastici → Regime variabile → Metodo simbolico → Numeri complessi

In questa pagina cerco di spiegare l'uso dei numeri complessi in un ambito particolare: l'analisi delle reti elettriche in regime sinusoidale.

Se siete interessanti ad una trattazione organica e rigorosa, è decisamente meglio consultare un libro di matematica, il vostro docente o, al limite, it.wikipedia.org/wiki/Numero_complesso.

Definizione

Un numero complesso in forma cartesiana è formato da due parti, una parte reale (in rosso) ed una parte immaginaria (in blu):

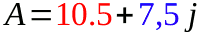
A=10.5+5,6j

La lettera j (nota 1), che permette di identificare la parte immaginaria, viene chiamata unità immaginaria ed è la soluzione... dell'equazione x² = -1; quindi:

j2=-1

Rappresentazione grafica

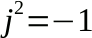
Un numero complesso può essere rappresentato in forma grafica. Utilizzando lo stesso numero di esempio ( A = 10.5 + 7.5j )

In orizzontale la parte reale, positiva e rossa in figura
In verticale la parte immaginaria, positiva e blu in figura

Nella figura sono rappresentati anche il modulo (in nero) e l'argomento, l'angolo evidenziato in verde. Per il loro calcolo è possibile usare il teorema di Pitagora oppure formule trigonometriche. Nell'esempio valgono:

Le quattro operazioni

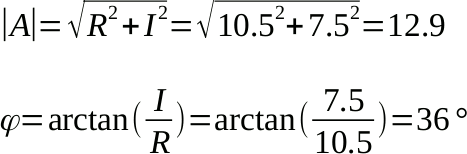
Come per tutti i numeri, dobbiamo capire come eseguire le quattro operazioni (nota 2). Come linea generale, è sufficiente trattare un numero complesso come un binomio e seguire le solite regole dell'algebra. Vediamo qualche esempio relativi ai due numeri:

A=2+3j
B=10-4j

Somma e sottrazione

Due operazioni semplici:

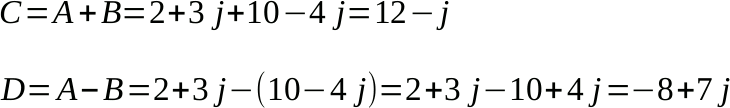
A+B e A-B

Moltiplicazione

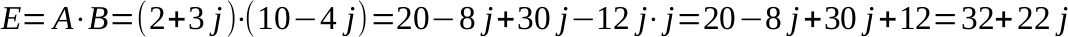
A per B

Un caso interessante si ha moltiplicando un numero complesso per il suo complesso coniugato, cioè per un numero con la stessa parte reale e parte immaginaria cambiata di segno.

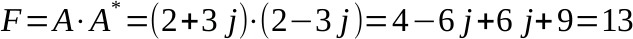
A per a*

Il fatto che il risultato sia un numero reale (parte immaginaria nulla) non è caso...

Divisione

Si tratta del passaggio più laborioso in quanto è necessario un passaggio di razionalizzazione per ottenere il risultato in forma cartesiana che consiste nel moltiplicare numeratore e denominatore per il complesso coniugato del denominatore.

A / B

Note

I matematici in genere preferisco la lettera i invece che j, ma in questo contesto esiste il rischio di confusione con la lettera I che indica la corrente
Sono ovviamente definite tutte le potenze, le radici, le funzioni trascendenti e tutti gli altri elementi tipici delle equazioni con i numeri reali, ma in questo contesto non siamo interessati a ciò

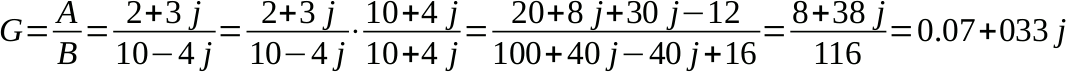
Data di creazione di questa pagina: aprile 2020
Ultima modifica: 30 aprile 2020