
Un segnale che varia nel tempo viene in genere descritto da un grafico che riporta in ascissa il tempo ed in ordinata la tensione oppure la corrente. In matematica è descritto da una funzione in cui la variabile indipendente è il tempo (t).
Il segnale esemplificativo descritto nel grafico seguente mostra una tensione che, in modo casuale, assume istante per istante valori compresi tra -20 V e +15 V.
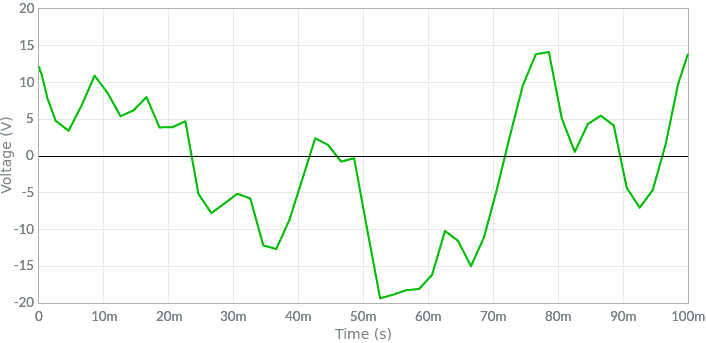
Le misure significative per questo segnale sono:
Per tutte le grandezza l'unità di misura è il volt (o l'ampere se si tratta di una corrente) e quindi occorre specificare quale grandezza intendiamo misurare.
Come caso particolare si definisce unipolare un segnale in cui la tensione (o la corrente ) è in ogni istante sempre positiva (oppure sempre negativa). In caso contrario, come nell'esempio, il segnale è detto bipolare.
Un segnale si dice periodico quando si ripete regolarmente nel tempo. Per esempio il segnale seguente si ripete uguale a sé stesso ogni millesimo di secondo.
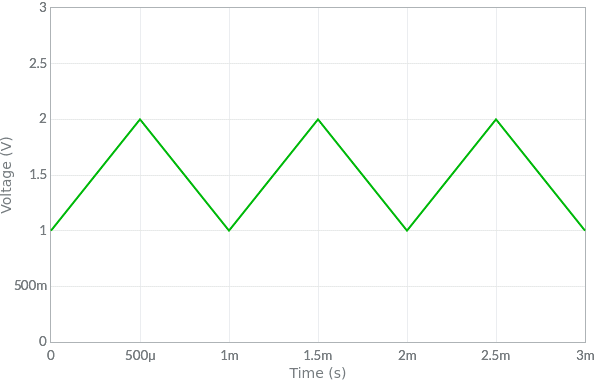
Le misure significative sono le stesse descritte nel paragrafo precedente a cui si aggiunge:
Nell'esempio mostrato si tratta di un segnale triangolare unipolare, in evidente riferimento alla forma ed al fatto che in ogni istante la tensione è positiva.
Il segnale sinusoidale è fondamentale ed è decritto nella pagina Segnale sinusoidale.
Il segnale ad onda rettangolare è fondamentale ed è descritto nella pagina Onda quadra.
La media tra un insieme di valori è un concetto intuitivo: si sommano i valori e si divide il risultato per il loro numero, concetto particolarmente familiare agli studenti.
L'estensione di tale concetto ai valori di una tensione (o una corrente) variabile nel tempo è formalmente dato dalla formula:
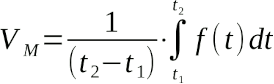
Purtroppo tale espressione matematica è (forse) comprensibile solo dagli studenti dell'ultimo anno della scuola superiore...
In alternativa possiamo pensare al grafico come costituito non da una linea, ma da numerosi punti equamente distanziati lungo l'asse orizzontale; il valor medio è la somma dei valori di tali punti diviso il numero di punti.
Un approccio rigoroso, ma relativamente elementare, fa riferimento alle aree invece che ai singoli valori numerici, considerando positive le aree sopra l'asse orizzontale e negative quelle al di sotto. Nella figura seguente sono state evidenziate in rosso le "aree positive", in blu quelle "negative". Il valor medio è la differenza tra le aree rosse e quelle blu, diviso il tempo di osservazione.
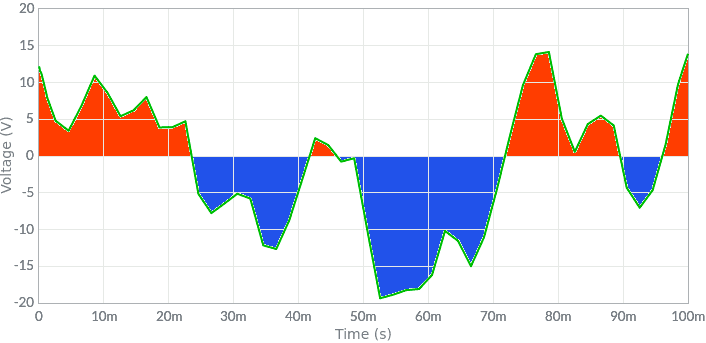
Nel caso di segnale periodico il calcolo può essere limitato ad un singolo periodo.
L'unità di misura del valor medio (VM o VDC) è il volt (o l'ampere, se si tratta di una corrente). Per evitare fraintendimenti è necessario specificare che si tratta di un valor medio.
Un segnale periodico con valore medio nullo si dice alternato.
In laboratorio il modo più utilizzato per misurare il valor medio è l'uso dell'apposita funzione presente in un oscilloscopio oppure l'uso di un multimetro impostato per misurare tensioni continue (DC). Analoghe tecniche vengono usate con i simulatori.
Il calcolo analitico può essere fatto manualmente solo in casi particolarmente semplici, come mostrato nei seguenti esempi.
Si consideri il segnale triangolare unipolare disegnato poco sopra.
L'area, in riferimento ad un singolo periodo, può essere calcolata come somma delle aree colorate evidenziate in corrispondenza del terzo periodo, tutte positive:
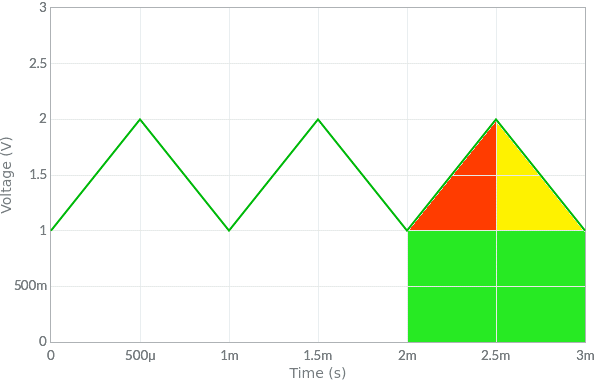
In questo caso, date le simmetrie presenti, il valor medio poteva essere calcolato intuitivamente, ma non è una regola generale, come mostrato nel seguente esempio.
Si consideri il seguente segnale rettangolare.
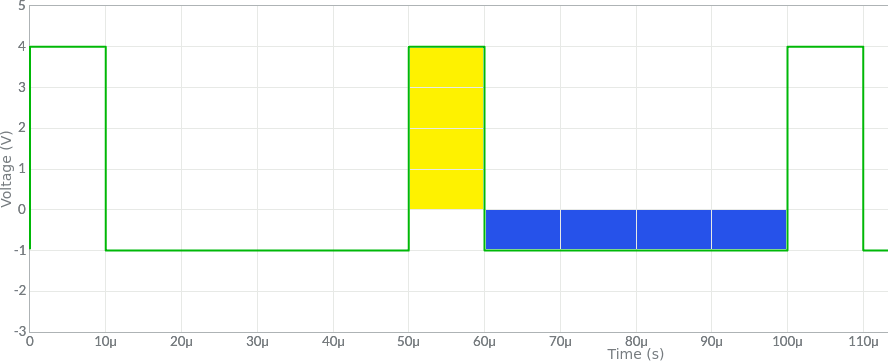
Il valor medio può essere calcolato sommando le aree positive (gialle) con le aree negative (blu), tenendo ovviamente conto del segno e dividendo per il periodo. In questo caso: VDC = (4·10e-6 + (-1)·40e-6) / 50e-6 = 0 V.
Il segnale ha valor medio nullo e si tratta quindi di un segnale alternato.
Questa grandezza misura gli effetti della tensione (o della corrente) ed ha molti nomi, da considerarsi tutti sinonimi: valore efficace, valor medio efficace (nota 2), tensione RMS (Root Mean Square), tensione True-RMS, VRMS, Veff...
La definizione formale è dato dalla formula:
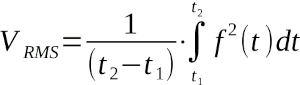
Purtroppo tale espressione matematica è (forse) comprensibile solo dagli studenti dell'ultimo anno della scuola superiore...
Più intuitivo legare la definizione di valore efficace alla potenza dissipata su un resistore da una tensione, indipendentemente dal fatto che tale tensione sia continua o variabile:
P = V2 / R
VRMS = √(P·R)
Per esempio una tensione continua di 10 V ai capi di un resistore da 100 Ω produce una potenza media di 1 W (P = V2 / R = 102 / 100 = 1 W). La stessa potenza (nota 1) è prodotta da una sinusoide con ampiezza efficace VRMS = 10 V o da un'onda rettangolare con ampiezza VRMS = 10 V.
Per evitare fraintendimenti, è utile, ma non obbligatorio, specificare che si tratta di un valore efficace. In effetti, se non diversamente specificato, la tensione di un segnale variabile è spesso indicata dalla sua tensione efficace.
In alcuni casi particolari potrebbe essere utile conoscere come calcolare il valore efficace in modo rapido:
In laboratorio il modo più utilizzato per misurare il valor medio efficace è l'uso dell'apposita funzione presente in un oscilloscopio i un un multimetro digitale, in genere indicata come True RMS (T-RMS). Analoghe tecniche vengono usate con i simulatori.
Il calcolo analitico può essere fatto manualmente solo in casi particolarmente semplici, come mostrato nel seguente esempio, non banale da comprendere.
Consideriamo il seguente segnale, applicato ad un resistore di valore 1 Ω (nota 3).
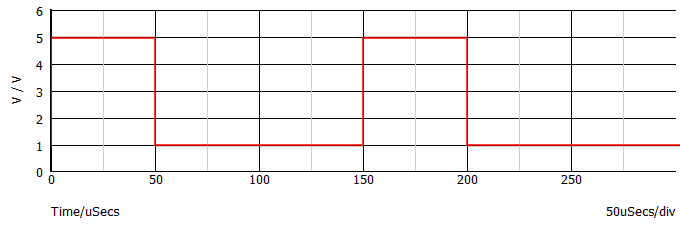
Il valor medio può essere calcolato come nei precedenti esempi 1 e 2. Esso vale VDC = 2,33 V.
Per il calcolo del valor medio efficace possiamo considerare il periodo del segnale diviso in due intervalli:
La potenza (media) in un periodo è la media pesata dei due valori precedenti: (25·50 + 1·100) / 150 = (1 250 + 100) / 150 = 9 W.
Applicando la formula che lega la potenza media al valor medio efficace abbiamo: VRMS = √9 = 3 V
Segnale a messaggio variabile sulla Highway 401 in Ontario, Canada - Vhayes1992 - CC BY-SA 4.0
Data di creazione di questa pagina: aprile 2020
Ultima modifica: 23 novembre 2024
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)