
I libri di fisica descrivono la potenza come l'energia che viene trasferita nell'unità di tempo. In particolare, in un circuito elettrico, i generatori introducono energia elettrica nel circuito e gli utilizzatori trasformano, a seconda dei casi, questa energia in calore, movimento, luce, suono...
In un circuito elettrico la potenza (istantanea) generata o utilizzata da un generico componente X è il prodotto della tensione ai capi del componente X e della corrente che scorre nel componente X:
PX = VX · IX
Un errore spesso fatto dai miei studenti: la potenza utilizzata da un ben determinato componente è il prodotto di una qualunque tensione per una qualunque corrente.
Si misura in watt (non in Watt, non in watts); il simbolo è W, senza punto finale.
Consideriamo un circuito costituito da un generatore di tensione collegato ad un resistore.
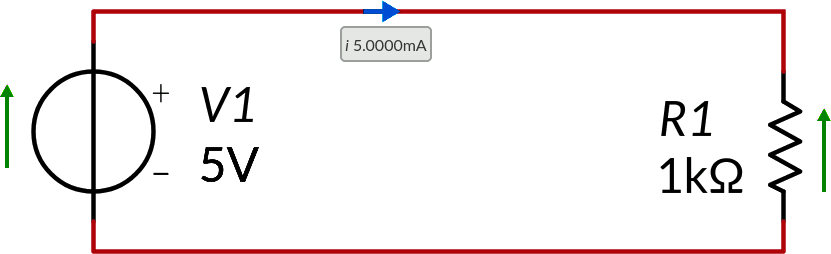
La tensione, in questo caso comune al generatore e al resistore, è 5 V.
La corrente, anch'essa in questo caso comune al generatore e al resistore, è 5 mA.
La potenza erogata dal generatore è:
P = V · I = 5 · 5·10-3 = 25·10-3 W
(o, meglio: P = 5 V · 5 mA = 25 mW nota 1)
Analogamente la potenza che il resistore trasforma in calore è:
P = V · I = 5 · 5 = 25 mW
Le formule precedenti sono corrette per qualunque tipo di circuito o di componente.
Solo per i resistori esistono due modi alternativi per calcolare la potenza:
PR = VR · IR = VR · VR / R = VR2 / R
Quest'ultime formule non sono certo necessarie, anche se a volte sono comode.
In questo caso: P = 52 / 1 = 25 mW (nota 1).
Trovare la potenza erogata dal generatore e quella dissipata dai tre resistori.
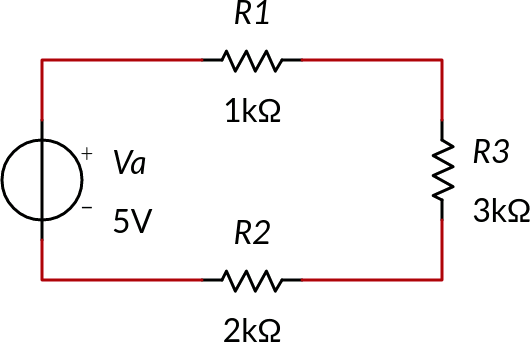
I tre resistori ed il generatore sono in serie. La corrente che li attraversa è:
I = 5 / (R1 + R2 + R3) = 0,83 mA
La potenza erogata dal generatore è:
PG = 5 · 0,83 = 4,2 mW
La tensione ai capi dei tre resistori (nota 3) è:
V1 = 0,83 · 1 = 0,83 V
V2 = 0,83 · 2 = 1.66 V
V3 = 0,83 · 3 = 2.49 V
La potenza dissipata dai tre resistori è:
P1 = V1 · I = 0,83 · 0,83 = 0.69 mW
P2 = V2 · I = 1,66 · 0,83 = 1,4 mW
P3 = V2 · I = 2,49 · 0,83 = 2.1 mW
Si noti che PG = P1 + P2 + P3; non è un caso!
Determinare la potenza erogata dal generatore e quella dissipata dai tre resistori

I quattro componenti sono in parallelo; la tensione ai loro capi coincide con quella del generatore VG = 5 V.
La potenza dissipata dai tre resistori è:
P4 = 52 / 3 = 8.3 mW
P5 = 52 / 2 = 12,5 mW
P6 = 52 / 1 = 25 mW
La corrente erogata dal generatore è:
IG = 5 / ( R4//R5//R6 ) = 9.2 mA
La potenza erogata dal generatore è:
PG = IG · VG = 5 · 9.2 = 46 mW
Si noti che, ovviamente, PG = P4 + P5 + P6.
Consideriamo il seguente circuito, formato da un generatore, un utilizzatore lineare (la resistenza) ed un utilizzatore non lineare (il LED). Il calcolo di tensioni e correnti non è qui affrontato e quanto indicato nello schema seguente può essere considerato un dato noto (nota 3).
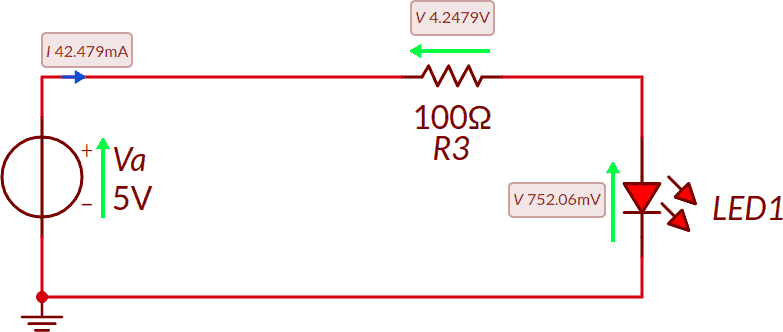
Tutti i componenti sono in serie e quindi sono attraversati dalla stessa corrente; vale circa 42,5 mA.
Si noti che la potenza fornita dal generatore coincide con la somma della potenza dissipata dagli utilizzatori. Ovviamente non è un caso.
Il concetto di potenza dissipata è strettamente legato a quello di efficienza energetica: quanta della potenza fornita dai generatori è effettivamente usata per scopi utili? Quanta invece è sprecata?
Consideriamo il precedente esempio. Il nostro interesse è accendere il LED: dei 212 mW generati da Va possiamo quindi considerare utile solo la potenza che arriva al LED, cioè 32 mW, circa il 15 % (nota 6); Il resto è sprecato in calore sulla resistenza. Si tratta quindi di un cattivo progetto, utilizzabile solo quando le potenze in gioco sono molto piccole e la semplicità di realizzazione è importante.
Diverso il caso in cui, con lo stesso circuito, vogliamo riscaldare l'ambiente: in questo caso è utile il calore generato dalla resistenza e quindi il rendimento dello stesso circuito diventa molto più elevato...
Consideriamo un generatore reale di tensione (nota 2) costituito da un generatore ideale (Vin nell'esempio, 5 V) e da una resistenza interna (Rin nell'esempio, 1 kΩ). Nello schema seguente è rappresentato all'interno del rettangolo grigio.
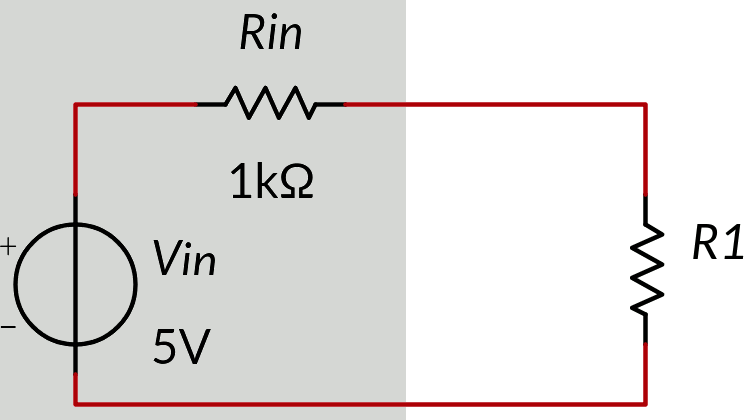
Colleghiamo ad esso un resistore R1, variabile.
La corrente I1 che scorre in R1 e la tensione V1 ai capi di R1 dipendono ovviamente dal valore di R1:
Graficamente:
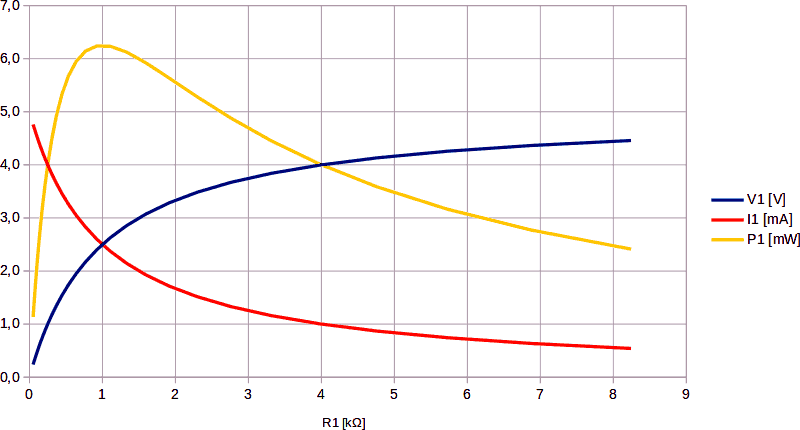
Dal grafico si vede come la potenza massima sia di 6,25 mW, in corrispondenza di R1 = 1kΩ. La stessa potenza è dissipata anche da Rin.
La conclusione è generale:
La condizione R1 = Rin è in molti contesti indicata come condizione di adattamento.
Utilizzando un programma di simulazione verificare sperimentalmente quanto affermato al paragrafo precedente. Qui una traccia per la verifica con l'uso di SIMetrix/SIMPLIS Elements.
Domanda che potrebbe sembrare un trabocchetto: data la resistenza R1 del carico (per esempio 100 Ω) quale valore deve assumere Rin per avere il massimo trasferimento di potenza a R1?
Riflessione: perché non è sempre una buona idea dal punto di vista del rendimento usare una resistenza di carico coincidente con la resistenza interna del generatore?
Data di creazione di questa pagina: febbraio 2022
Ultima modifica: 11 ottobre 2023
La fotografia di apertura è un notturno di Potenza.
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)