
In questa pagina sono descritti il segnale ad onda rettangolare ed in segnale ad onda quadra.
Il segnale rettangolare (o anche onda rettangolare) è un segnale periodico caratterizzato da due livelli di tensione (High e Low). Il passaggio tra i due livelli è molto rapido, idealmente istantaneo.
Il segnale rettangolare è di particolare importanza perché permette di rappresentare due tipi di segnali importanti a livello applicativo:
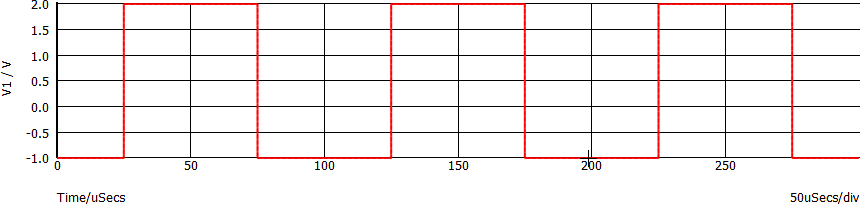
Il grafico seguente mostra nel dominio del tempo un segnale rettangolare (nota 3):
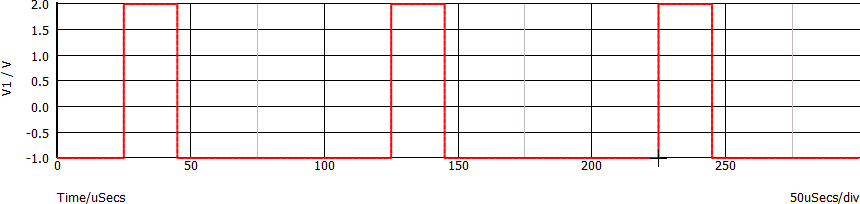
Le sue caratteristiche:
| T | Period o Cycle Time (periodo) | 100 µs |
| TON, TH | High Pulse Width o semplicemente Width (durata dell'impulso alto ) | 20 µs |
| TOFF, TL | Low Pulse Width (durata dell'impulso basso) | 80 µs |
| VON, VH | High level (livello alto) | 2 V |
| VOFF, VL | Low level (livello basso) | -1 V |
Spesso vengono indicate anche altre caratteristiche, derivate dalle precedenti
| f | Frequency (frequenza) | 1 / T | 10 kHz |
| DC% | Duty Cycle o semplicemente Duty (ciclo utile) | TON / T · 100 | 20 % |
Il valor medio è -0,4 V. Il calcolo è poco intuitivo e può essere fatto con il metodo descritto in questo esempio, anche se in genere si preferisce far uso di strumenti di calcolo automatici.
Ancora meno intuitivo è il calcolo del valor medio efficace (VRMS), pari a circa 1,25 V. Il calcolo può essere fatto con il metodo descritto in questo esempio, anche se in genere si preferisce far uso di strumenti di calcolo automatici.
Nel mondo reale un segnale ad onda rettangolare nel dominio del tempo appare su un oscilloscopio come rappresentato nell'immagine esemplificativa seguente:
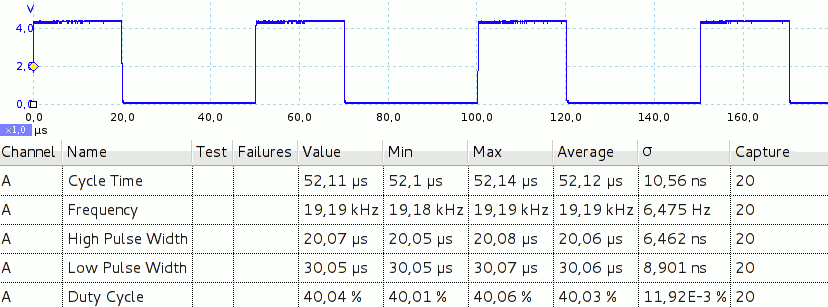
Nella parte bassa dell'immagine alcune misure fatte automaticamente dallo strumento, in questo caso un Picoscope 3405A.
Come dimostrato dal teorema delle serie di Fourier, lo spettro del segnale rettangolare è formato da:
L'ampiezza delle linee spettrali ha un andamento che, qualitativamente, è quello della funzione y = |sinc(x)| cioè:
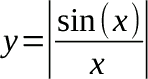
Il grafico qualitativo di questa funzione è il seguente:
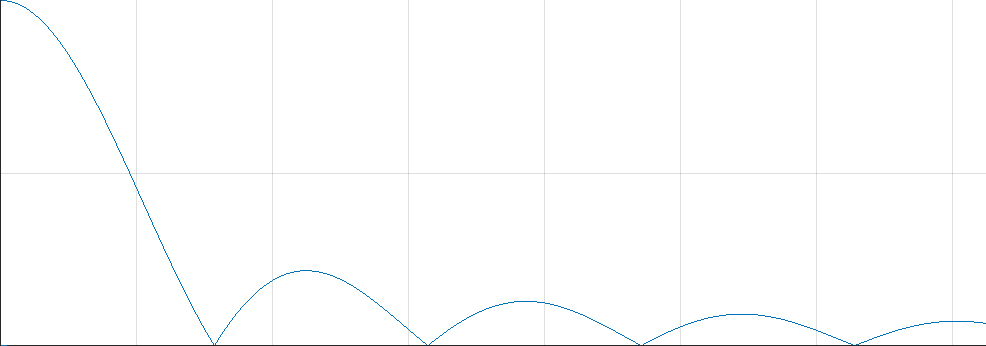
Tale grafico è (immaginate una palla che cade e rimbalza su un pavimento):
Questo grafico costituisce l'inviluppo dello spettro, cioè quella linea immaginaria che racchiude tutte le linee spettrali presenti (nota 6).
Nello spettro del segnale rettangolare, l'asse orizzontale riporta la frequenza in hertz ed i punti in cui l'inviluppo si annulla sono f = 1 / TON e suoi multipli interi.
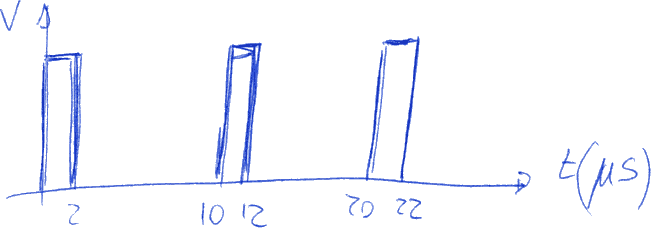
Un'onda rettangolare ha TON = 0,02 ms e frequenza pari a 10 kHz.
Nel dominio del tempo ha il seguente grafico:
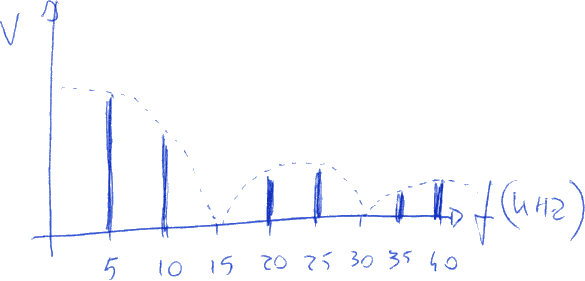
Nel dominio della frequenza ha il seguente grafico:
Le ampiezza mostrate sono state ottenute con un programma di simulazione; le formule relative possono essere considerate, nel contesto in cui questi appunti sono stati scritti, come un contenuto avanzato.
Utile un confronto tra questo spettro e quello dell'onda quadra, caso particolare dell'onda rettangolare. In particolare: perché nello spettro dell'onda quadra sono assenti le linee spettrali con frequenza multipla intera pari di quella della fondamentale?
Dato il seguente grafico semi-quantitativo (nota 5):
Dato il seguente grafico semi-quantitativo (nota 5):
Un'onda rettangolare ha T = 1 ms e TON = 0,25 ms
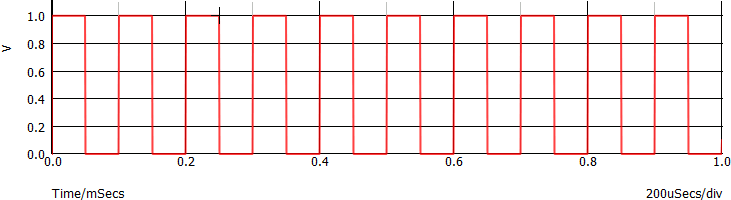
Un caso particolare di onda rettangolare è l'onda quadra, caratterizzata dal fatto da TON = TOFF (evidentemente DC = 50 %). Di seguito un esempio:
Come dimostrato dal teorema delle serie di Fourier, lo spettro dell'onda quadra è formato da:
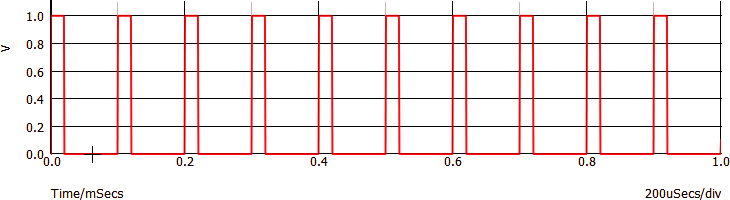
Un'onda quadra ha frequenza f = 10 kHz; VH = 1 V; VL = 0 V. L'ampiezza picco-picco dell'onda quadra è quindi di VPP = 1 V:
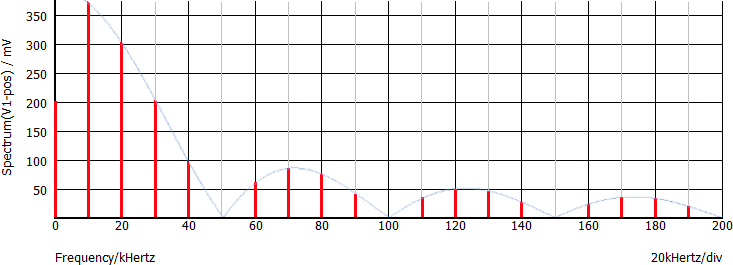
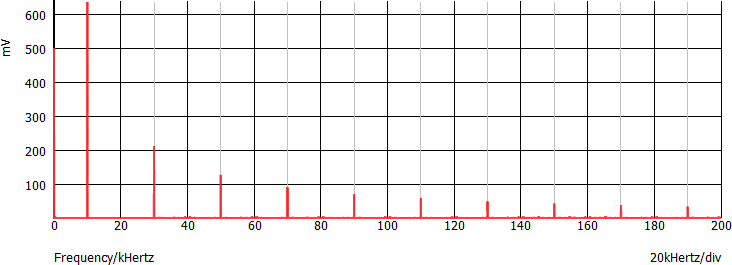
Lo spettro del segnale è formato da linee con frequenza 10 kHz, 30 kHz, 50 kHz... e ampiezza rispettivamente 0,64 V, 0,21 V, 0,13 V... Inoltre è presente una linea con "frequenza 0" e ampiezza di 500 mV (valor medio):
In particolare abbiamo:
Si consideri la seguente onda quadra (nel dominio del tempo):
Si consideri la seguente onda quadra, disegnata nel dominio della frequenza:
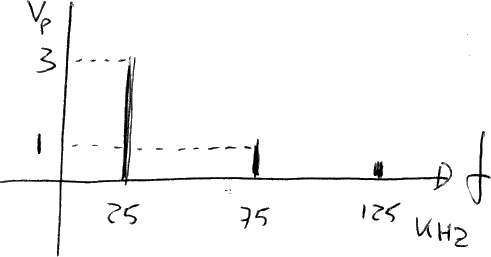
Un'onda quadra ha VH = 3.3 V e VL = 0 V. La sua frequenza è f = 1 MHz.
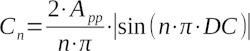
Quadra Turbo-R V-Tech. Autore e licenza d'uso non noti.
Pagina creata nell'aprile 2023
Ultima modifica: 13 ottobre 2025
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)