Serie di Fourier

Home → Tutorial → Appunti scolastici → Regime variabile → Serie di Fourier

Alla pagina Somma di sinusoidi è mostrato come la somma di più sinusoidi produca segnali non sinusoidali. Un quesito interessante è il passaggio opposto: dato un generico segnale non sinusoidale, possiamo immaginarlo come somma di tante sinusoidi?

Ovviamente la risposta è si... altrimenti questa pagina non avrebbe ragion d'essere (nota 1).

Per chi utilizza i metodi dell'analisi matematica, l'operazione di scomporre un generico segnale in somma di tante sinusoidi è complessa e classificata tra gli argomenti piuttosto avanzati, perlomeno per la scuola superiore; il risultato è orgogliosamente mostrato dai due personaggi della fotografia di apertura. Questa scomposizione prende il nome di serie di Fourier o, per i segnali non periodici, trasformata di Fourier. La loro rappresentazione grafica prende il nome di spettro.

In realtà l'analisi spettrale è il modo naturale e più semplice con cui, per esempio, l'essere umano sente i suoni, vede i colori, descrive il movimento dei pianeti. Purtroppo posizioni oscurantiste di pensatori del passato, da Galileo (nota 2) a Lagrange (nota 3), hanno reso difficile ai più descrivere come è fatta la realtà...

Serie di Fourier

Enunciato del teorema delle Serie di Fourier: qualunque segnale periodico, continuo e limitato, con frequenza f₀, può essere ottenuto sommando:

una costante, pari al valor medio del segnale
una serie di sinusoidi con frequenza multipla intera di f₀ e ampiezza e fase calcolabile con apposite formule, qui non descritte

Vediamo alcuni esempi di segnali, limitandoci ad una rappresentazione grafica (spettro), ignorando la fase e, a volte, formule e numeri.

I grafici qui mostrati sono stati ottenuti attraverso un programma di simulazione.

Esempio 1

Consideriamo il segnale rappresentato nel dominio del tempo dal seguente grafico:

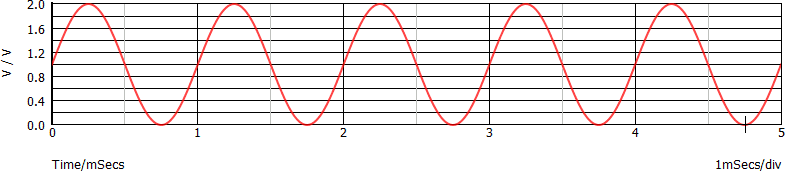
Sinusoide con offset

Il segnale è evidentemente periodico (T = 1 ms; f = 1 kHz), limitato tra le tensioni di 0 V e 2 V, continuo, cioè può essere disegnato senza staccare la matita dal foglio. Il teorema di Fourier è quindi applicabile

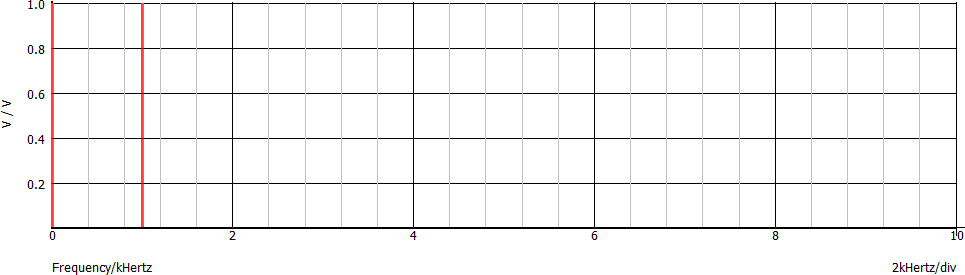
É forse l'unico caso in cui è possibile con il solo intuito arrivare alla scomposizione del segnale in serie di Fourier: si tratta infatti della somma di:

una sinusoide con frequenza 1 kHz, ampiezza picco-picco di 2 V, ampiezza di picco 1 V, fase nulla
una tensione continua pari ad 1 V (offset oppure valor medio)

Disegniamo lo spettro corrispondente, somma degli spettri dei due segnali sopra descritti:

lo spettro della sinusoide è disegnato seguendo queste indicazioni
lo spettro di un segnale continuo è una linea verticale lungo l'asse verticale e lunghezza pari alla tensione. In un certo senso: una sinusoide con frequenza... 0

Spettro di una sinusoide con offset

Esempio 2

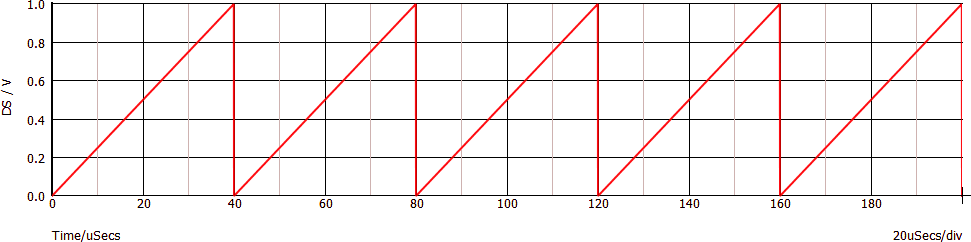
Consideriamo un segnale a denti di sega (nota 7) con frequenza pari a 25 kHz, cioè con periodo di 40 µs. Il nome deriva, come facilmente intuibile, dalla forma che il segnale assume nel dominio del tempo:

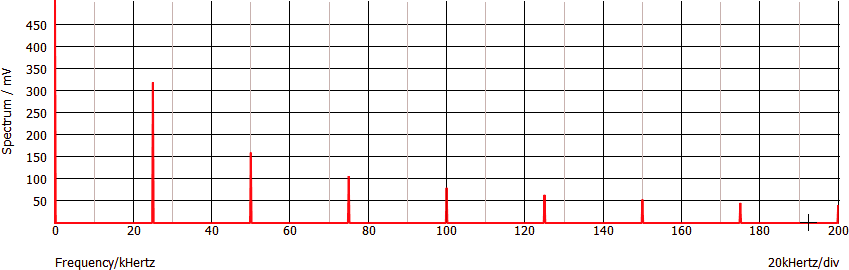
In base al teorema di Fourier lo spettro del segnale è formato da linee di frequenza pari alla frequenza del segnale e suoi multipli interi: 25 kHz, 50 kHz, 75 kHz... Occorre poi aggiungere una linea con "frequenza 0" e ampiezza pari al valor medio del segnale, 500 mV in questo esempio.

In questo sito non sono riportate formule o altri metodi analitici per calcolare l'ampiezza delle linee spettrali diverse dal valor medio. Se interessa: it.wikipedia.org/wiki/Onda_a_dente_di_sega.

Segnale a denti di sega

Esempio 3

Consideriamo un segnale triangolare (nota 7) con frequenza 30 kHz, cioè con periodo di 33,3 µs. Il nome deriva, come facilmente intuibile, dalla forma che il segnale assume nel dominio del tempo:

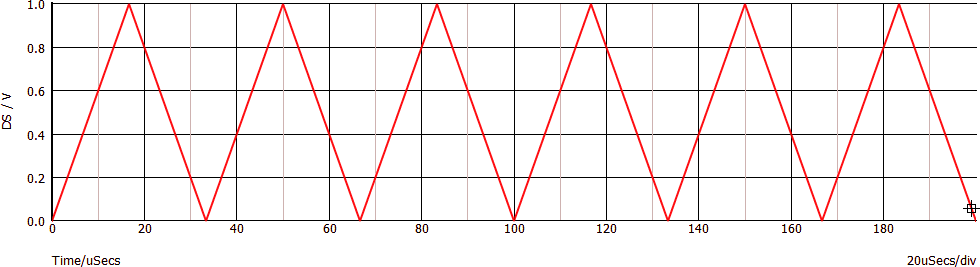
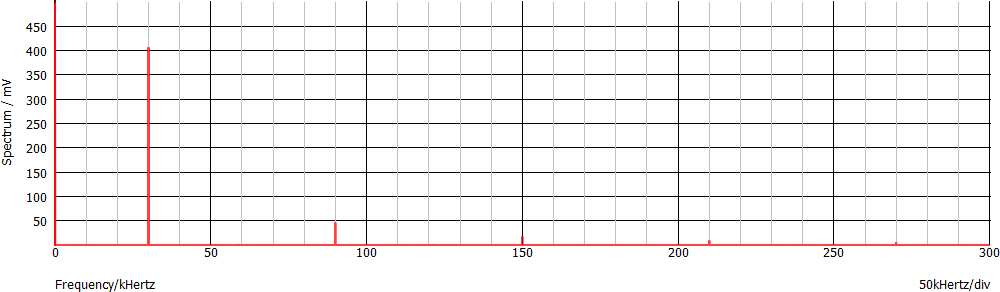
In base al teorema di Fourier lo spettro del segnale è formato da linee di frequenza pari alla frequenza del segnale e suoi multipli interi: 30 kHz, 90 kHz, 150 kHz... Occorre poi aggiungere una linea con "frequenza 0" e ampiezza pari al valor medio del segnale, 500 mV in questo esempio.

In questo sito non sono riportate formule o altri metodi analitici per calcolare l'ampiezza delle linee spettrali diverse dal valor medio. Se interessa: it.wikipedia.org/wiki/Onda_triangolare.

Spettro del segnale triangolare

Onda quadra

Questo segnale, a differenza dei precedenti, ha notevolissima importanza e quindi è descritto in una pagina specifica: Onda quadra.

Conclusione

Conclusione, di carattere generale e valida per qualunque segnale periodico:

Lo spettro di un qualunque segnale periodico con frequenza f è costituito da linee verticali con frequenza multipla intera della frequenza f del segnale: f, 2·f, 3·f. Alcune di queste linee spettrali possono non essere presenti
Lo spettro contiene oltre alle linee di cui al punto 1 una linea verticale posta nell'origine, il valor medio
Nell'ordine abbiamo quindi nello spettro di un segnale periodico:
- Il valor medio, sempre con frequenza zero. L'ampiezza dipende dal segnale e può anche essere 0
- La fondamentale, con frequenza pari a quella del segnale. L'ampiezza dipende dal segnale
- Le armoniche, con frequenza pari a multipli interi della fondamentale. L'ampiezza dipende dal segnale e può, per alcune linee spettrali, essere 0

Note

Chiedo scusa a chi ha qualche competenza matematica per le approssimazioni, le imprecisioni ed anche gli errori concettuali che introduco: i destinatari di questa pagina sono gli studenti della prima classe del triennio di scuola superiore, quindi con competenze matematiche modeste
Come per esempio spiegato da Giovanni Schiaparelli, Galileo non comprese che il modello tolemaico del sistema solare è una rappresentazione geometrica delle serie di Fourier. La cosa è peraltro ignota ancora oggi alla quasi totalità delle persone che si ritengono istruite
Lagrange ed altri insigni matematici contestarono pesantemente il lavoro di Fourier per questioni formali, probabilmente senza comprenderne il senso
In alternativa alla potenza a volte è presente il valore efficace al quadrato
Formula a rigore valida solo per i resistori
Ovviamente in questo caso non vale il teorema di Parseval, perlomeno così come è stato scritto. Perché?
Il segnale non è continuo, ma con qualche forzatura, il teorema è applicabile
Quello mostrato è in realtà uno spettro logaritmico

Pagina creata nell'ottobre 2020
Ultima modifica: 7 maggio 2025