Spettro di potenza

Home → Tutorial → Appunti scolastici → Regime variabile → Spettro di potenza

Segnali periodici

Vediamo alcune forme che può assumere lo spettro di un segnale periodico.

Tensioni efficaci

Lo spettro di un segnale periodico può riportare, invece del valore massimo, il valore efficace. Il grafico non cambia molto:

il numero e la frequenza delle linee spettrali non cambia
il valor medio non cambia. Per un segnale continuo infatti valor medio, valore massimo e valore efficace coincidono
le linee corrispondenti alla fondamentale e alle armoniche diventano 1,41 volte più piccole in ampiezza. Infatti per la sinusoide V_RMS = V_P / √2

Esempio 1

Consideriamo un'onda quadra con frequenza 1 kHz e ampiezza compresa tra 0 V e 5 V. Lo spettro dei valori di picco può essere disegnato come descritto in questa pagina:

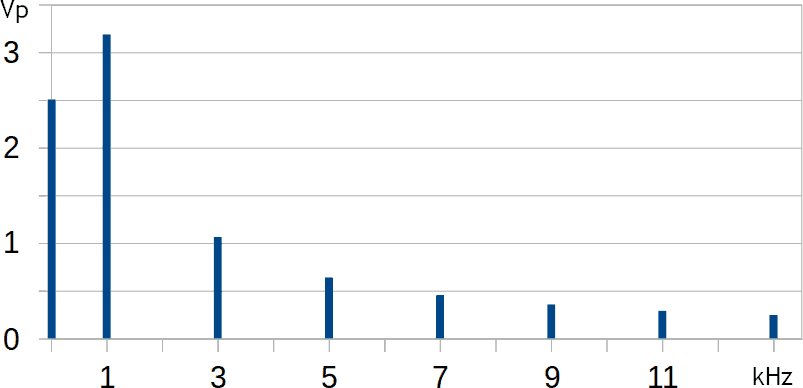
Spettro dei valori di picco

Lo spettro che riporta la tensione efficace è mostrato di seguito:

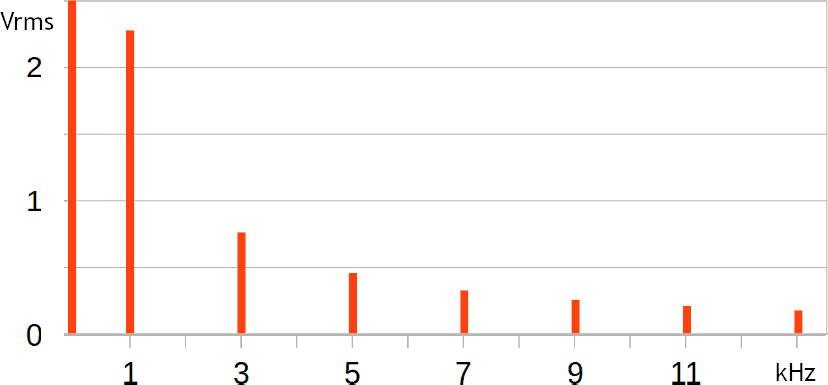
Spettro dei valori efficaci

Tale grafico è simile al precedente, semplicemente le linee spettrali sono più piccole di un fattore √2 (ad esclusione di quella del valor medio, che rimane invariata); tutte le frequenze rimangono invariate.

Potenze

Lo spettro di un segnale periodico può riportare, invece delle tensioni, le potenze delle linee spettrali (nota 1). La forma del grafico, dal punto di vista qualitativo, non cambia in modo sostanziale:

il numero e la frequenza delle linee spettrali non cambia
invece del valor medio (se presente) è riportata la sua potenza:

P₀ = V_M² / R

invece dell'ampiezza di picco delle sinusoidi, la corrispondente potenza:

P = V_RMS² / R = V_P² / 2 / R (nota 2)

Esempio 2

Consideriamo lo stesso segnale descritto nell'esempio 1. Questo segnale è applicato ad un resistore di 1 kΩ. Ricordando che P = V_RMS² / R possiamo calcolare la potenza delle singole linee spettrali:

F [ kHz]	Vp [V]	Vrms [V]	P [mW]
-	2,50	2,50	6,25
1	3,18	2,25	5,07
3	1,06	0,75	0,56
5	0,64	0,45	0,20
7	0,45	0,32	0,10
9	0,35	0,25	0,06
11	0,29	0,20	0,04
13	0,24	0,17	0,01

Il grafico seguente mostra lo spettro della potenza. Le singole linee mantengono la frequenza presente nei due grafici precedenti, mentre l'ampiezza è stata sopra calcolata:

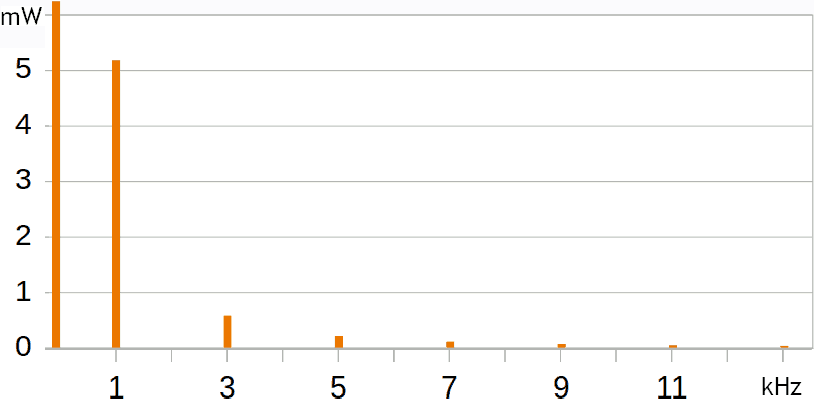
Si noti che solo le prime linee spettrali possono essere facilmente visualizzate sul grafico: tolte le prime tre o quattro, le altre appaiono infatti piccolissime e praticamente tutte uguali tra di loro.

Teorema di Parseval

Enunciato: la potenza di un segnale periodico è pari alla somma delle potenze delle sue linee spettrali.

Esempio 3

La potenza del segnale descritto nell'esempio 1 può essere calcolato con il teorema di Parseval, sommando i valori calcolati nell'esempio 2:

P = 6,25 + 5.07 + 0.56 + 0.20 + 0.10 + 0.06 + 0.04 + 0.01 = 12,3 mW

Tale valore è molto vicino a quello che si ottiene calcolando direttamente la potenza dell'onda quadra, pari a 12,5 mW. La potenza "mancante" può essere facilmente spiegata considerando che le linee spettrali dell'onda quadra sono infinite ed in questo esempio abbiamo sommato solo le prime 8.

Scala logaritmica

L'operazione di elevare al quadrato per calcolare le potenze esalta la differenza tra le grandezze più piccole e quelle più grandi, come si vede chiaramente grafico trovano con l'esempio 2.

Questo comportamento può essere corretto con l'uso di una scala logaritmica, ricorrendo all'uso del dBm.

La forma del grafico appare piuttosto diversa:

il numero e la frequenza delle linee spettrali non cambia rispetto ai grafici precedenti
l'ampiezza delle linee è calcolata come P_dBm = 10 · log(P)
l'asse orizzontale non viene disegnato in corrispondenza di 0 dBm, ma viene scelto un valore più piccolo della potenza più piccola da disegnare, scegliendo un valore multiplo di 10, spesso negativo

Esempio 4

Consideriamo lo stesso segnale descritto negli esempi precedenti. La potenza in unità logaritmiche è calcolata nella seguente tabella:

F [ kHz]	Vp [V]	Vrms [V]	P [mW]	P [dBm]
-	2,50	2,50	6,25	8
1	3,18	2,25	5,07	7
3	1,06	0,75	0,56	-2
5	0,64	0,45	0,20	-7
7	0,45	0,32	0,10	-10
9	0,35	0,25	0,06	-12
11	0,29	0,20	0,04	-14
13	0,24	0,17	0,03	-15

La potenza più piccola è -15 dBm; scegliamo quindi come base del grafico -20 dBm (ma anche -30 dBm potrebbe essere adeguato). Tutte le linee verticali partono dalla base del grafico, non da 0 dBm.

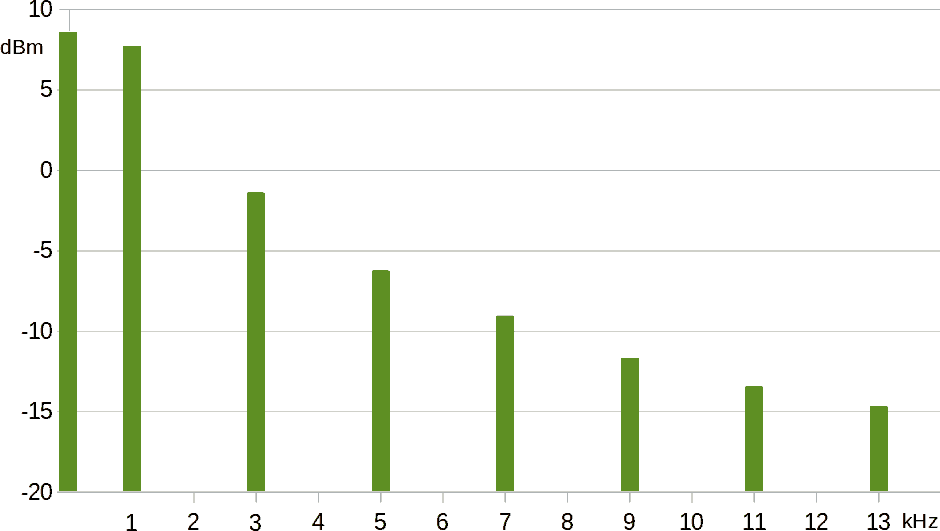
Spettro di potenza in dBm

Attenzione se si applica il teorema di Parseval a grandezza espresse in dBm: sommare logaritmi significa infatti moltiplicare il loro argomento!

Segnali non periodici

Nel caso di segnali non periodici, lo spettro di potenza, analogamente allo spettro della tensione, assume la forma di una superficie:

L'asse verticale riporta la densità spettrale di potenza, misurata un W/Hz
L'asse orizzontale riporta la frequenza

Il teorema di Parseval calcola la potenza come area della superficie.

Esempio 5

Un segnale ha il seguente spettro di potenza. Si noti come sull'asse verticale è evidenziato che l'unità di misura è watt su hertz.

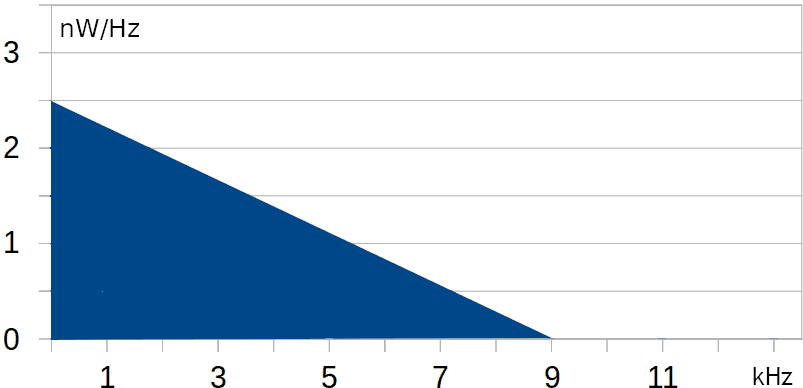
Spettro segnale non periodico

La potenza del segnale può essere calcolata con le usuali regole della geometria elementare (A = base · altezza / 2):

P = 2,5 · 9 / 2 = 11,25 µW

Esempio 6

Un segnale casuale non è periodico ed ha ampiezza istantanea casuale. Si può dimostrare che il suo spettro è una superficie rettangolare con base infinita:

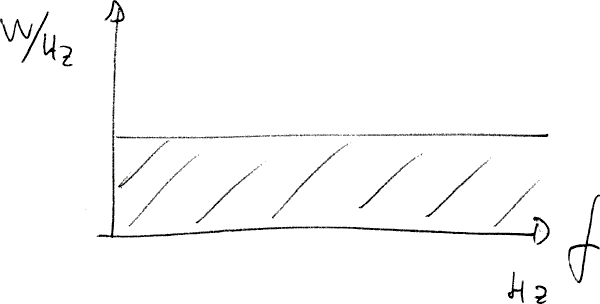
Spettro segnale casuale

Il teorema di Parseval afferma che la potenza di tale segnale può essere calcolata moltiplicando l'altezza del rettangolo (finita) per la sua base (infinita), producendo un'area infinita, cioè una potenza infinita. La cosa ovviamente è impossibile dal punto di vista fisico...

Note

La potenza può essere calcolata nel caso di carichi resistivi come P = V² / R. La tensione da utilizzare è quella efficace
Formula valida solo se cos(φ) = 1
Ovviamente in questo caso non vale il teorema di Parseval, perlomeno così come è stato scritto. Perché?
Il valore in dBm nella parte bassa del grafico è liberamente scelto per essere inferiore alla più piccola delle linee spettrale presenti

Pagina creata nel settembre 2023
Ultima modifica: 20 agosto 2025

Probabilmente anche a Potenza esistono leggende di spettri, ma di sicuro i fantasmi di Roma della fotografia di apertura sono più famosi.