

Spesso nella definizione di grandezze elettriche (e non solo) vengono usati i logaritmi, normalmente in base 10. Nei sistemi di telecomunicazioni, questa è quasi la regola.
Qualche ragione di questa scelta:
Un asse con scala logaritmica (nota 10) appare come in figura, disegnato con tratti neri:

Nell'ambito delle tecnologie elettroniche gli assi logaritmici sono spesso usati per rappresentare le frequenze, ma si trovano anche per tensioni, potenze o tempi.
Spesso le grandezze elettriche vengono espresse in unità logaritmiche (nota 9), utilizzando il decibel (dB) ed altre unità da esso derivate.
Il dB è la decima parte del bel (nota 11) e misura su scala logaritmica il rapporto fra due grandezza omogenee dal punto di vista dimensionale, per esempio due potenze. In generale può essere definito come:
RdB = 10 · log ( P1 / P2 )
Si noti che il dB, essendo il logaritmo di una quantità adimensionale, a sua volta non ha un'unità di misura; è però necessario scrivere sempre "dB" per indicare che si tratta di una grandezza logaritmica e non lineare.
Le unità qui descritte sono relative a tensioni e potenze e non verrà per esempio illustrato come sono utilizzate nella misura della pressione acustica.
Il valore ottenuto da un logaritmo è, per definizione, adimensionale, ma, scegliendo opportunamente la potenza P2 al denominatore può esprimere un valore assoluto.
Il dBm (o, più correttamente dal punto di vista formale, dBmW) misura la potenza su scala logaritmica; è definito come
PdBm = 10 · log10 |PW / 1 mW|
oppure, in modo poco rigoroso, ma comodo, come PdBm = 10 · log10 |PmW| .
Il dBm è l'unità di misura più usata nell'ambito delle telecomunicazioni per esprimere le potenze.
Esempi:
I dBW misurano la potenza su scala logaritmica; sebbene ampiamente utilizzate in alcuni ambiti, in queste pagine non troverete molte applicazioni che ne fanno uso.
Sono definiti (nota 8) come
PdBW = 10 · log10 |PW|
Esempi:
Per i dBW valgono le stesse osservazioni riportate più avanti in merito ai dBm
Attività: utilizzare le formule inverse per verificare i precedenti esempi.
Alcune osservazione che, pur essendo già contenute nelle formule matematiche, sono utili nelle applicazioni:
II dBV misura la tensione su scala logaritmica; è definito (nota 7) come;
VdBV = 20 · log10 |VV|
Attenzione al 20 presente nella formula (nota 1)!
Esempi:
Attività: utilizzare le formule inverse per verificare i precedenti esempi.
Il dBµV (a volte anche dBµ) misura la tensione su scala logaritmica; sebbene ampiamente utilizzato in alcuni ambiti, in queste pagine non troverete molte applicazioni che ne fanno uso.
Viene definito come
VdBµV = 20 · log10 |VV / 1 µV|
oppure, in modo poco rigoroso, ma comodo, come VdBµV = 20 · log10 |VµV|.
Esempi:
Attività: utilizzare le formule inverse per verificare i precedenti esempi.
Il dBu misura la tensione efficace su scala logaritmica; sebbene ampiamente utilizzato, in particolare in campo audio, in queste pagine non troverete molte applicazioni che ne fanno uso.
Viene definito come
VdBu = 20 · log10 |VV / 0,77 V|
Esempi:
Utilizzare le formule inverse per verificare tutti i precedenti esempi.
Il decibel è l'unità logaritmica per misurare il guadagno di un quadripolo.
Se ingresso e uscita sono entrambe potenze, il guadagno in decibel è definito come (nota 1):
GdB = 10 · log ( PO / PI )
Per le proprietà dei logaritmi possiamo scrivere la seguente relazione usando esclusivamente unità logaritmiche (nota 4):
GdB = PO [dBm] - PI [dBm]
Se ingresso e uscita sono entrambe tensioni, il guadagno in decibel è definito come:
GdB = 20 · log ( VO / VI )
Per le proprietà dei logaritmi (prodotti e divisioni che divengono somme e sottrazioni) possiamo scrivere la seguente relazione usando esclusivamente unità logaritmiche (nota 4):
GdB = VO [dBV] - VI [dBV]
Osservazioni:
La tensione efficace (spesso sottointeso) in ingresso ad un quadripolo vale 2 mV, quella in uscita 1 V, sempre efficace. Tutte le resistenza di ingresso ed uscita al quadripolo sono uguali e pari a 50 Ω. Determinare il guadagno di tensione e di potenza, in unità lineari e logaritmiche.
Per quanto riguarda il guadagno di tensione, rispettivamente in unità lineari e logaritmiche:
GV = VOUT/VIN = 1 V / 0.002 V = 500
VIN = 20 log (0,002) = −54 dBV
VOUT = 20 log (1) = 0 dBV
GdB = VOUT - VIN = 0 dBV - (-54 dBV) = 54 dB
Osservazione: 20 log (500) = 54 dB
Per quanto riguarda il guadagno di potenza, rispettivamente in unità lineari e logaritmiche (nota 3) :
PIN = VIN2 / R = 0,000004 / 50 = 0,00000008 W = 0,00008 mW = -41 dBm
POUT = VOUT2 / R = 20 mW = 13 dBm
GP = POUT / PIN = 20 mW / 0.00008 mW = 250 000
GdB = POUT - PIN = 13 dBm - (-41 dBm) = 54 dB
Osservazione 1: 10 log(250 000) = 54 dB
Osservazione 2: il guadagno di potenza e quello di tensione, se espressi in unità logaritmiche, coincidono numericamente e come "unità di misura" nelle condizioni date (quadripolo adattato).
L'attenuazione è l'inverso del guadagno. Qui una spiegazione dettagliata.
Se si usano unità logaritmiche, l'attenuazione è l'opposto del guadagno (nota 6):
αdB = VI [dBV] - VO [dBV] = -GdB
αdB = PI [dBm] - PO [dBm] = -GdB
Spesso più quadripoli sono collegati in cascata.
Il guadagno complessivo (in dB) è pari alla somma dei singoli guadagni (sempre in dB).
GdB = G1dB + G2dB + G3dB...
Se per alcuni quadripoli è data l'attenuazione, questa va sottratta:
GdB = G1dB - α2dB + G3dB...
La tensione di ingresso di un quadripolo vale 2 V, quella in uscita 1 V. Tutte le resistenza di ingresso ed uscita al quadripolo sono uguali e pari a 50 Ω. Determinare l'attenuazione di tensione e di potenza, in unità lineari e logaritmiche.
Per quanto riguarda l'attenuazione di tensione, rispettivamente in unità lineari e logaritmiche:
αV = VIN/VOUT = 2 V / 1 V = 2 (adimensionale!)
VIN = 20 log (2) = 6 dBV
VOUT = 20 log (1) = 0 dBV
αdB = VIN - VOUT = 6 dBV - 0 dBV = 6 dB
Osservazione: 20 log (2) = 6 dB
Per quanto riguarda l'attenuazione di potenza, rispettivamente in unità lineari e logaritmiche:
PIN = VIN2 / R = 80 mW = 19 dBm (nota 5)
POUT = VOUT2 / R = 20 mW = 13 dBm
αP = PIN / POUT = 4 (adimensionale!)
αdB = PIN - POUT = 19 - 13 = 6 dB
Osservazione 1: 10 log(4) = 6 dB
Osservazione 2: l'attenuazione di potenza e quella di tensione, se espresse in unità logaritmiche, coincidono numericamente e come "unità di misura" nelle condizioni date (quadripolo adattato).
Questi grafici sono utilizzati per rappresentare:
Un grafico è detto semilogaritmico se:
Potete scaricare un file contenete:
Come spesso avviene, i grafici sono "in bianco", sia per quanto riguarda i numeri che le unità di misura, e devono essere completati in base alla situazione concreta.
Un segnale è somma di tre sinusoidi con frequenza 100 Hz, 2 000 Hz e 50 kHz. La potenza è, rispettivamente, 10-4 W, 10 µW e 1 mW.
Di seguito lo spettro su un grafico semilogaritmico, ottenuto dopo aver trasformato le tre potenze nelle equivalenti unità logaritmiche:
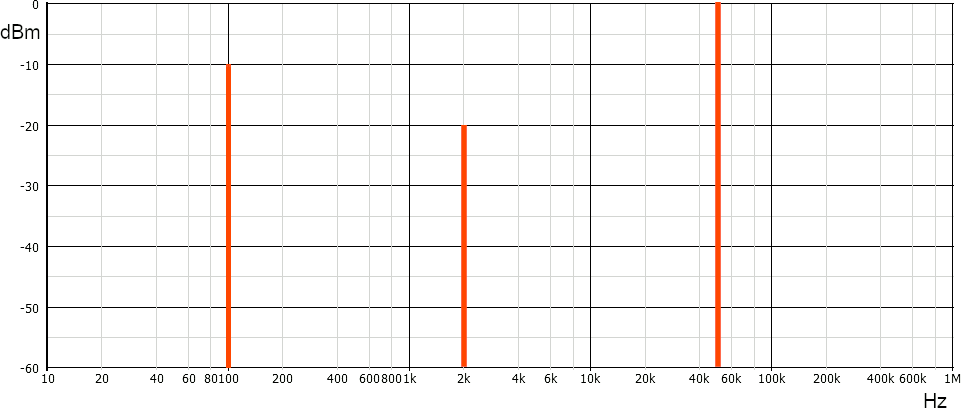
La scelta dai valori minimi e massimi da riportare sugli assi dipende ovviamente dal segnale rappresentato. Non esistono regole, se non il buon senso; per esempio anche la rappresentazione seguente è corretta (e migliore).
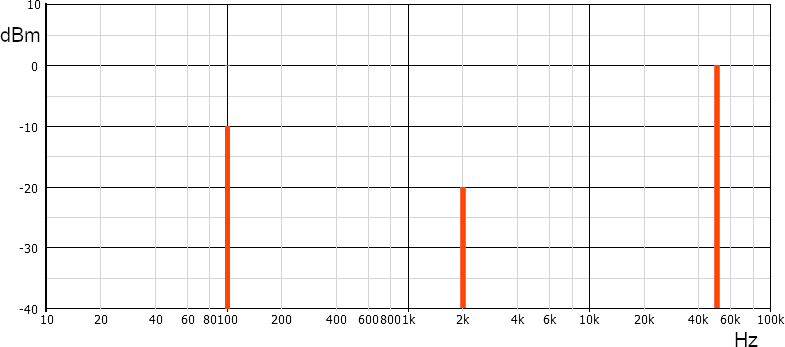
Da evitare invece grafici che rappresentano le linee troppo vicino ai bordi, in quanto di più difficile lettura. Per esempio, sempre in riferimento all'esempio, è bene evitare di scegliere come frequenza minima 100 Hz o come potenza minima -20 dBm.
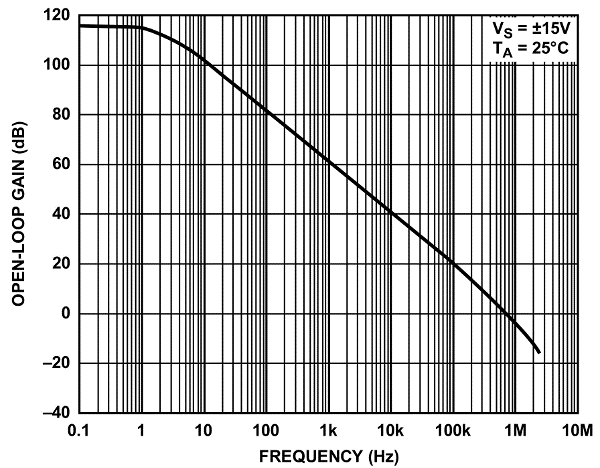
Il seguente grafico ottenuto sperimentalmente mostra il guadagno di un circuito in funzione della frequenza.
Alcune formule di uso comune non sono utilizzabili quando le grandezze sono espresse in unità logaritmiche. Tre casi importanti:
Il motivo deriva direttamente dalle proprietà dei logaritmi ed in particolare dal fatto che prodotti e rapporti tra grandezze lineari diventano somme e differenze usando grandezze logaritmiche.
Pagina creata nel gennaio 2013
Ultima modifica: 29 settembre 2025
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)