
Come studiare un circuito in cui sono presenti più di un generatore di tensione sinusoidale? Se il circuito è lineare, il modo più semplice è applicare il principio di sovrapposizione degli effetti. Occorre poi utilizzare alcune formule trigonometriche e studiare la funzione corrispondente. Oppure, più semplicemente, utilizzare le trasformate di Fourier.
In questa pagine cercherò di usare esclusivamente grafici e considerazioni qualitative per arrivare ad una rappresentazione di segnali complessi come somma di molte sinusoidi, con l'obbiettivo di facilitare lo studio dei sistemi di telecomunicazioni.
Consideriamo il seguente circuito:
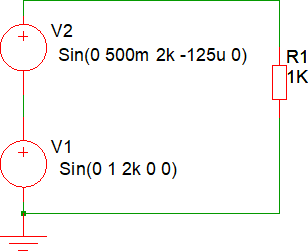
Sono presenti i due generatori sinusoidali V1 (frequenza 2 kHz, ampiezza 1 V) e V2 (frequenza 2 kHz, ampiezza 500 mV, in anticipo di 125 µs, nota 1). Il grafico nel dominio del tempo di queste due tensioni è il seguente:
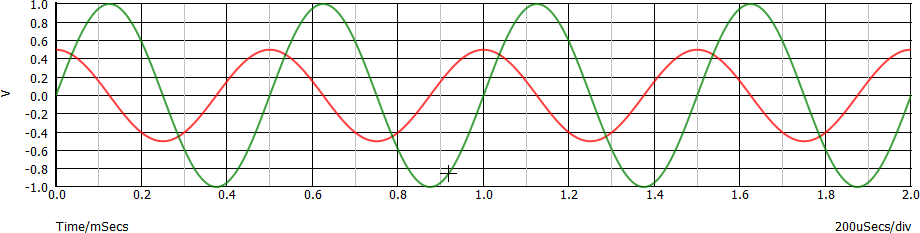
I due generatori sono in serie e quindi per ottenere la tensione applicata ad R1 basta sommare punto per punto i due grafici. Per esempio:
Di seguito il grafico complessivo, con in blu la tensione somma:
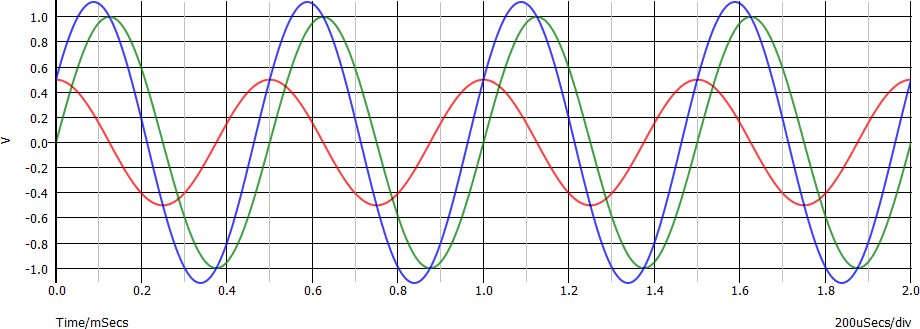
Conclusione, con validità generale per la somma di segnali sinusoidali con la stessa frequenza: la tensione somma è una sinusoide con la stessa frequenza delle sinusoidi sue componenti. Per chi è interessato, ampiezza e fase della somma posso essere calcolate con formule trigonometriche oppure (consigliato) usando i numeri complessi ed applicando quanto qui descritto..
Consideriamo lo stesso schema precedente, ma con due generatori sinusoidali con le seguenti caratteristiche:
Il grafico di queste due tensioni è il seguente:
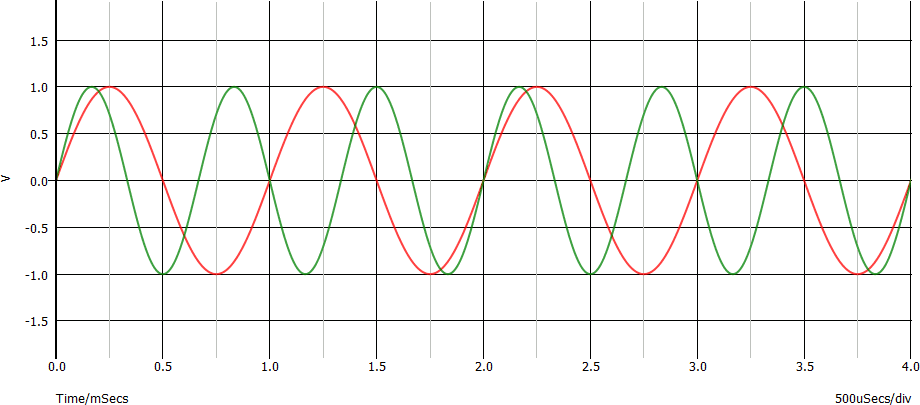
La somma di queste due sinusoidi è complessa da immaginare (ed anche da disegnare per via analitica...). Ci viene in aiuto il software di simulazione:
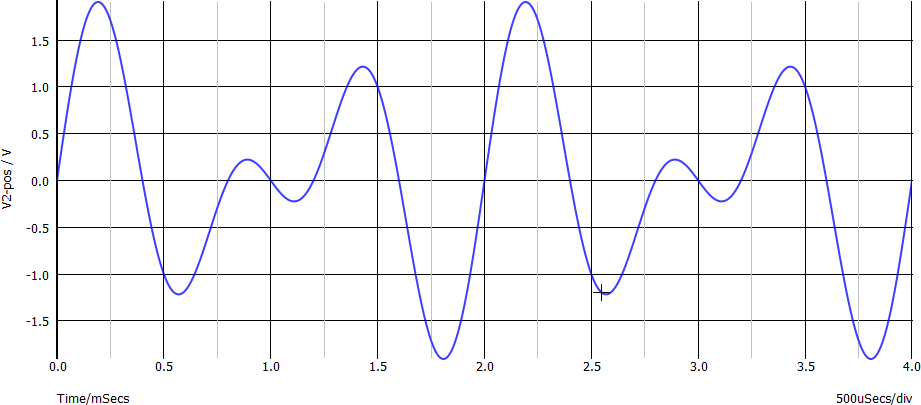
Si noti che tale segnale è periodico con frequenza 500 Hz e non sinusoidale.
Conclusione, con validità generale per la somma di segnali sinusoidali con frequenza diversa: la tensione somma è un segnale variabile, non sinusoidale, con frequenza pari al Massimo Comun Divisore delle frequenze delle sinusoidi sue componenti.
Non molto diverso dal precedente il caso in cui le due sinusoidi sommate hanno una frequenza multipla intera dell'altra. Consideriamo:
Di seguito i grafici di tali tensioni:
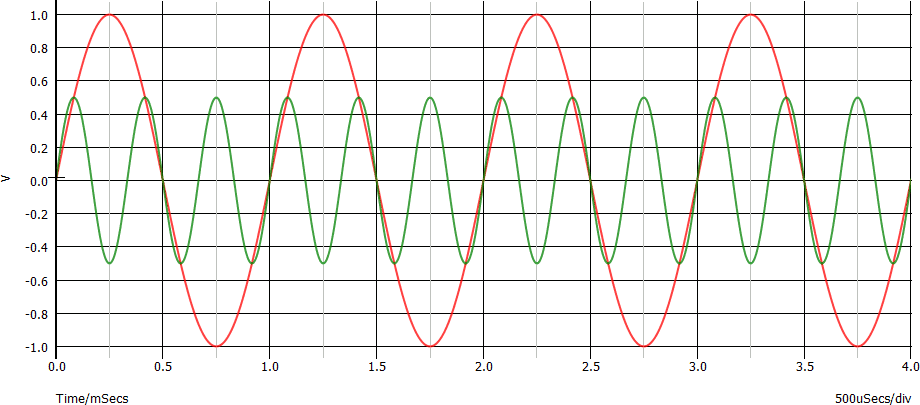
La somma di queste due sinusoidi è complessa da immaginare (ed anche da disegnare per via analitica...). Ci viene in aiuto il software di simulazione:
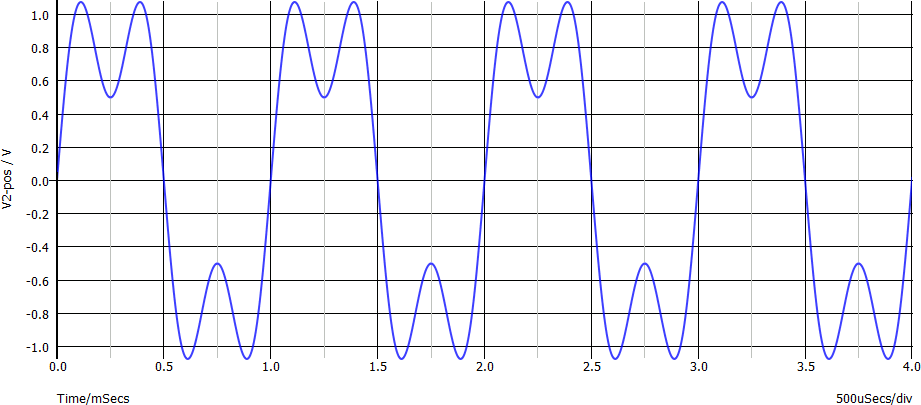
Si noti la frequenza pari ad 1 kHz.
Conclusione, con validità generale per la somma di segnali sinusoidali con frequenza multipla intera: la tensione somma è un segnale variabile, non sinusoidale, con frequenza pari a quella della sinusoide con frequenza inferiore. Le singole linee spettrali sono chiamate armoniche; la prima armonica è chiamata fondamentale oppure prima armonica, le successive sono numerate seconda armonica (frequenza doppia della fondamentale), terza armonica (frequenza tripla) ecc.
Come appena visto, la rappresentazione nel dominio del tempo della somma di sinusoidi è attività complessa.
Decisamente più semplice e comprensibile la rappresentazione nel dominio della frequenza.
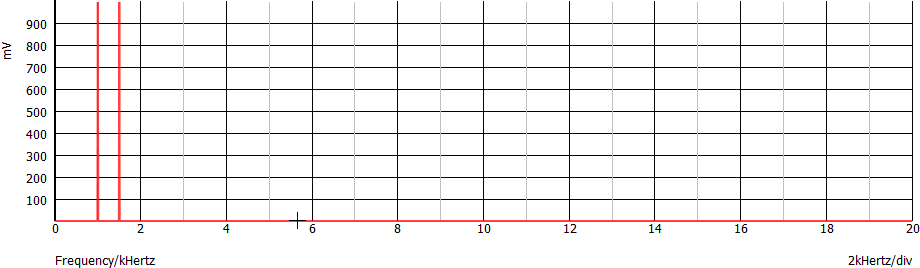
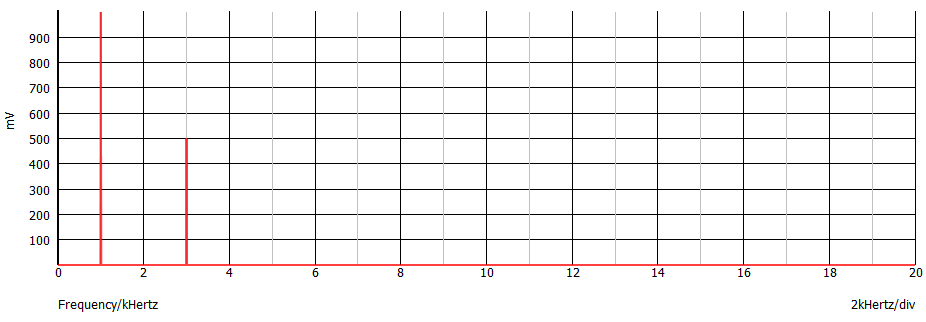
Vediamo gli spettri dei tre segnali descritti in precedenza:
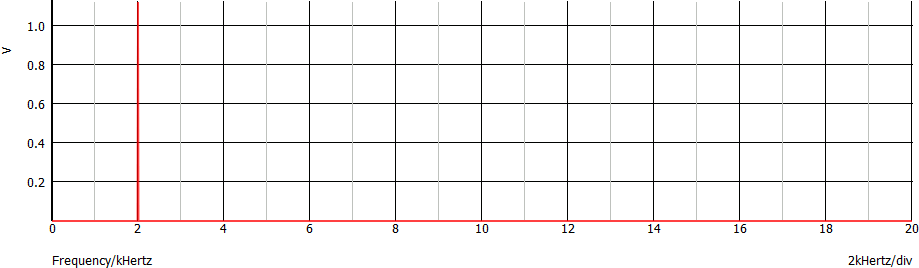
Data di creazione di questa pagina: settembre 2020
Ultima modifica: 10 settembre 2022
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)