

Il principio di sovrapposizione (degli effetti) è applicabile esclusivamente ai circuiti lineari contenenti almeno due generatori di tensione e/o corrente (nota 1). A queste condizioni è possibile studiare separatamente l'effetto dei singoli generatori presenti sapendo che l'effetto complessivo è pari alla somma algebrica dei effetti dei singoli generatori.
In pratica:
Per annullare un generatore:
Il fatto che questo principio sia applicabile esclusivamente ai circuiti lineari, può essere usato come definizione rigorosa di circuito lineare: un circuito è lineare se ad esso è applicabile il principio di sovrapposizione degli effetti.
Consideriamo il seguente circuito e calcoliamo la tensione V3 ai capi di R3 e la corrispondente corrente I3. I risultati sono già mostrati nello schema.
Innanzitutto osserviamo che il principio di sovrapposizione è applicabile: il circuito contiene solo resistori e generatori di tensione e quindi è lineare.
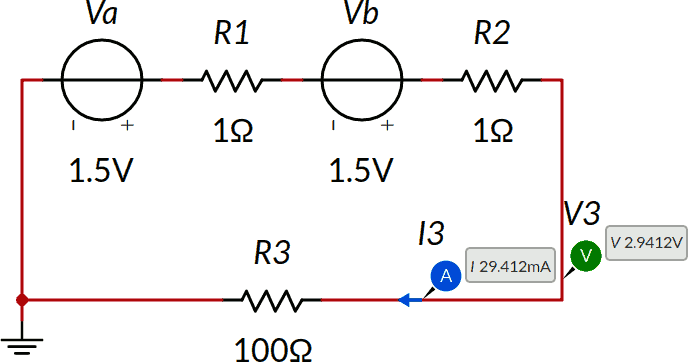
Nella fotografia di apertura trovate un'applicazione nel mondo reale: due pile AAA in serie sono state schematizzate come due generatori reali di tensione con Vin = 1,5 V (nello schema: Va e Vb) e resistenza interna Rin = 1 Ω (nello schema: R1 e R2). Chiunque le abbia mai usate per alimentare un circuito sa per esperienza che la tensione in uscita è circa 3 V (nota 2).
Annulliamo Vb, lasciando la sua resistenza interna R2, e calcoliamo I'3. Si noti che I3 è stata indicata con un singolo apice, per evidenziare che è solo parte del risultato.
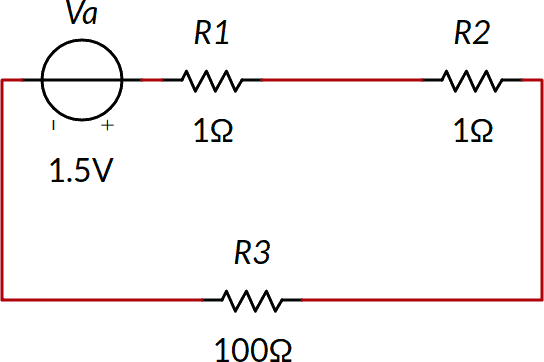
La corrente in R3 si calcola molto velocemente osservando che R1, R2 ed R3 sono in serie:
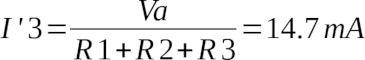
Il procedimento lo stesso: annulliamo Va e calcoliamo I''3, indicata con un doppio apice.
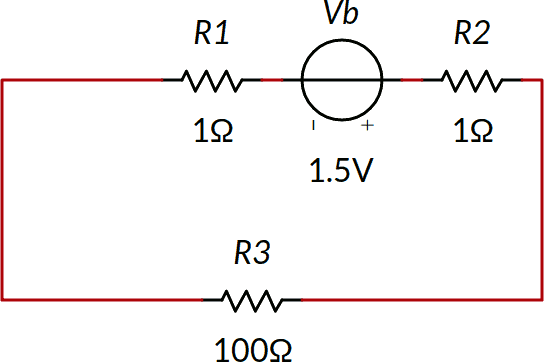
Il circuito è praticamente identico al precedente, come pure il risultato. Quindi:
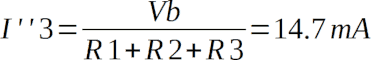
La corrente nel circuito originario è pari alla somma algebrica delle due correnti trovate:
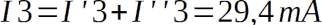
La tensione ai capi di R3 la possiamo calcolare applicando la legge di Ohm; vale 2,94 V.
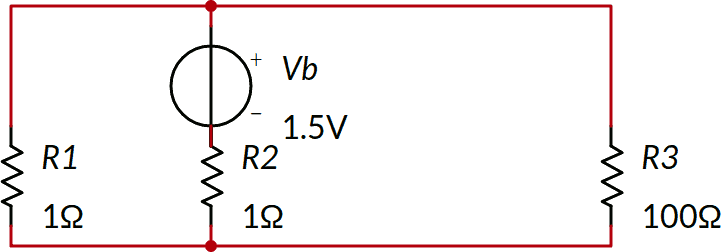
Consideriamo il seguente circuito e calcoliamo la tensione V3 ai capi di R3 e la corrispondente corrente I3. Anche in questo caso i risultati sono già mostrati nello schema.
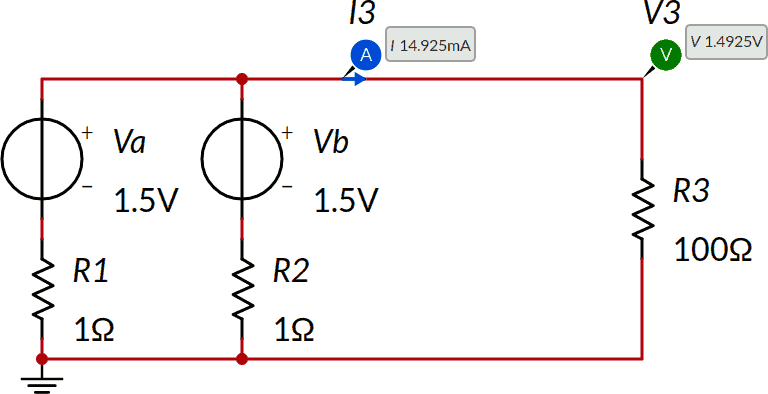
Innanzitutto osserviamo che il principio di sovrapposizione è applicabile: il circuito contiene solo resistori e generatori di tensione e quindi è lineare.
Potrebbe trattarsi di due pile in parallelo, configurazione molto meno frequente della precedente.
Annulliamo Vb e calcoliamo la tensione V'3 ai capi di R3; il circuito corrispondente è il seguente.
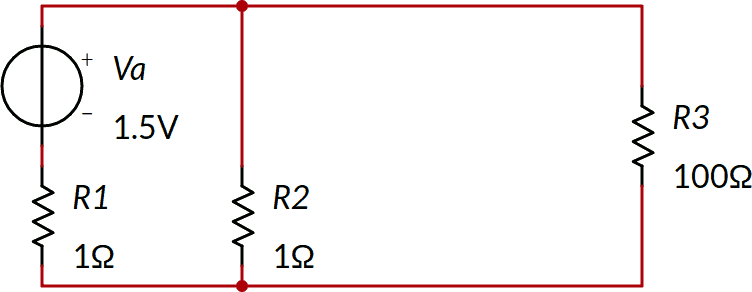
Per la risoluzione possiamo utilizzare uno qualunque dei metodi noti; ne vengono mostrati tre: iniziamo applicando la legge di Ohm ed in seguito, per ottenere lo stesso risultato, utilizzeremo il teorema di Thévenin oppure i principi di Kirchhoff. Ovviamente è sufficiente scegliere una sola delle tre strade mostrate ed altre ancora se ne potrebbero trovare, ma una cosa è certa: tutte devono portare allo stesso risultato!
R2 ed R3 sono in parallelo. R23, parallelo di R2 ed R3, è circa 0.99 Ω.

R1 e R23 sono in serie.

La corrente in R123 è 0,754 A (legge di Ohm); anche la corrente in R23 è 0,754 A: R1 e R23 sono infatti in serie.
La tensione ai capi di R23 è 0.746 V (legge di Ohm); anche la tensione ai capi di R3 è 0,746 V: R2 ed R3 sono infatti in parallelo.
Quindi V'3 = 0,746 V. Per la legge di Ohm I'3 = 7,46 mA.
Un metodo alternativo per calcolare I'3 e V'3: possiamo applicare il teorema di Thévenin trasformando il bipolo alla sinistra della linea tratteggiata verde nel corrispondente generatore reale, trovando VEQ ed REQ, e quindi trovare la corrente in R3.
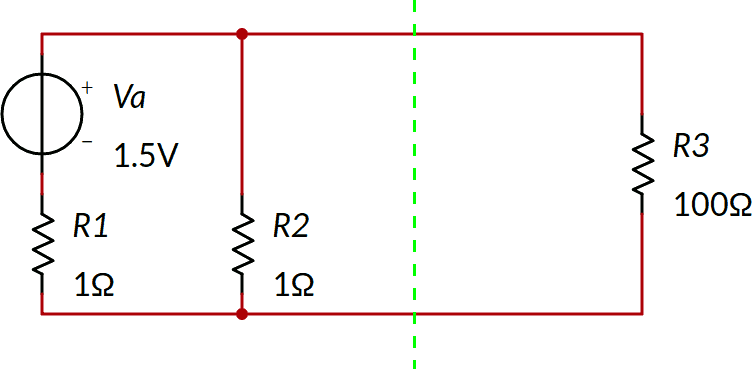
La tensione equivalente e la resistenza equivalente secondo Thévenin del bipolo a sinistra valgono VEQ = 0,75 V e REQ = 0,5 Ω. Il calcolo è lasciato come esercizio. (nota 3)
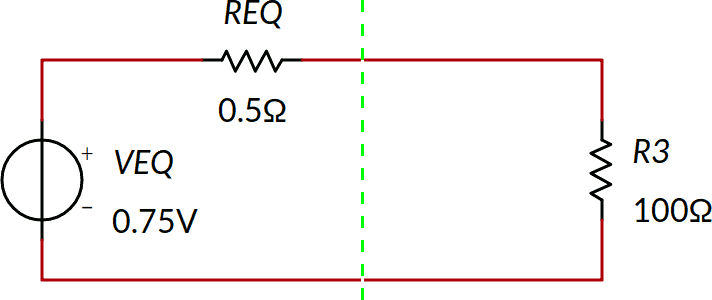
R3 ed REQ sono in serie (R3EQ = 100,5 Ω) e quindi, applicando la legge di Ohm, I'3 = 7,46 mA; evidentemente è lo stesso valore calcolato precedentemente.
Una terza strada per trovare I'3 e V'3: possiamo applicare i principi di Kirchhoff (nota 4).
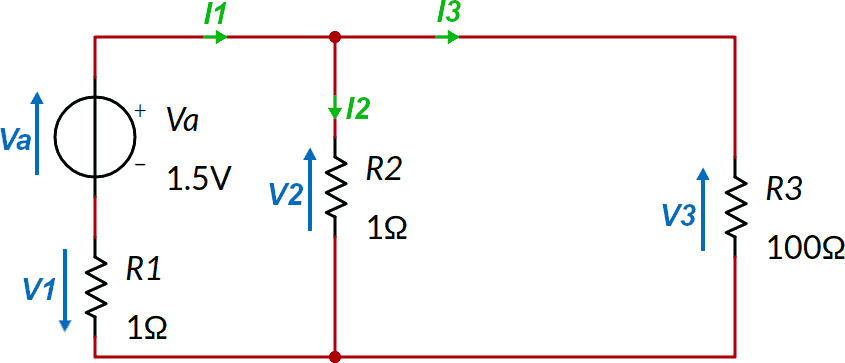
Dopo aver indicato sullo schema tensioni (in blu) e le correnti (in verde) scriviamo il sistema da risolvere, nelle tre incognite I1, I2 ed I3:
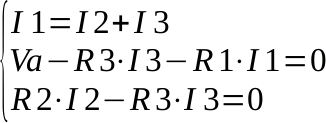
Dalla seconda equazione ricaviamo I1:
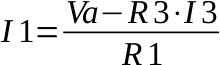
Dalla terza ricaviamo I2:
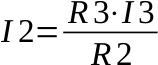
Sostituiamo nella prima e ricaviamo I3:

Con i dati forniti ricaviamo I'3 = 7,46 mA, valore ovviamente coincidente con quanto precedentemente calcolato.
R1 e R3 sono in parallelo e, rifacendo uno degli stessi procedimenti visti nel punto precedente, troviamo che V'3 = 0,746 V, cosa peraltro ovvia, viste le disposizioni dei componenti e l'identico valore.
La tensione ai capi di R3 nel circuito originale è quindi pari alla somma di V'3 e V''3: V3 = 1,49 V
I3 è pari a 14,9 mA (legge di Ohm).
Consideriamo il seguente circuito e calcoliamo la tensione VLED ai capi del LED e la corrispondente corrente ILED. Anche in questo caso i risultati sono già mostrati nello schema.
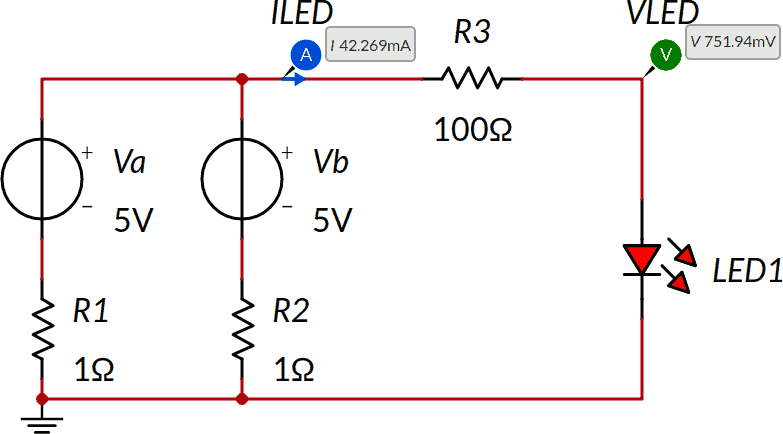
Il principio di sovrapposizione non è applicabile: il circuito contiene infatti un LED, elemento non lineare. Una soluzione alternativa è presentata con questo esempio.
Consideriamo il seguente circuito e calcoliamo la corrente I3. Anche in questo caso il risultato è già mostrato nello schema.
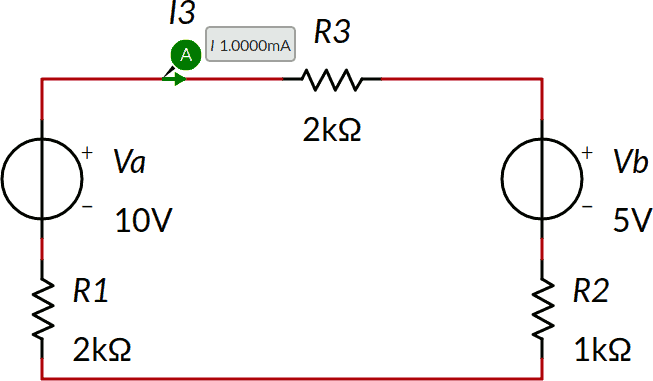
Innanzitutto osserviamo che il principio di sovrapposizione è applicabile: il circuito contiene solo resistori e generatori di tensione e quindi è lineare.
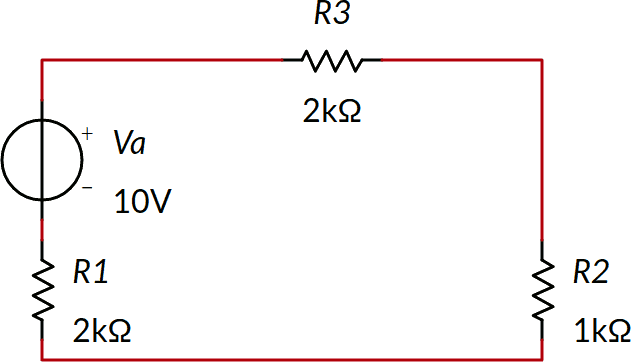
Abbiamo un generatore di tensione da 10 V e tre resistenze in serie, pari a 5 kΩ. La corrente I'3 è quindi di 2 mA, con verso orario.
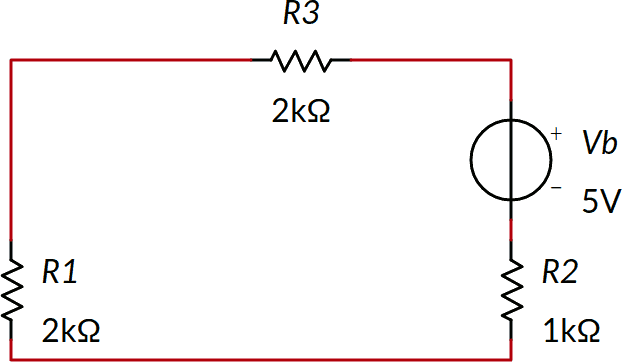
Abbiamo un generatore di tensione da 5 V e tre resistenze in serie, pari a 5 kΩ. La corrente I''3 è quindi di 1 mA, con verso antiorario.
La corrente complessiva è pari a I3 = I'3 + I''3 = 2 - 1 = 1 mA, in senso orario. Si noti che i versi delle due correnti I'3 e I''3 sono opposti e quindi la somma algebrica si è tradotta in una differenza.
In questo circuito Vb ha il verso della tensione opposto a quello della corrente, non rispettando la convenzione dei generatori. Motivare questa apparente contraddizione.
Quanto vale la corrente se Va = Vb?
Data di creazione di questa pagina: novembre 2019
Ultima modifica: 21 novembre 2019
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)