Trasformata di Fourier

Home → Tutorial → Appunti scolastici → Regime variabile → Trasformata di Fourier

In questa pagina sono affrontate, in modo assolutamente superficiale, le trasformate di Fourier, viste come estensione ai segnali non periodici delle Serie di Fourier.

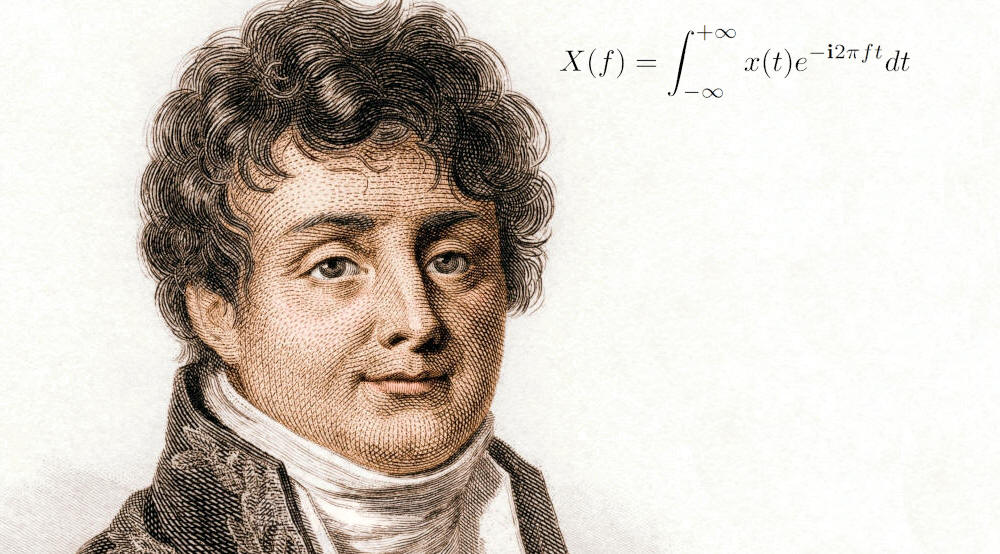
Il ritratto un po' sornione che apre questa pagina è di Jean Baptiste Joseph Fourier, matematico francese che dopo essere sopravvissuto al Terrore e alle fatiche delle diplomazia napoleonica, ebbe il tempo di rivoluzionare la matematica e le sue applicazioni fisiche.

Il teorema delle serie di Fourier è applicabile solo a segnali periodici. Se il segnale è non periodico occorre passare alle trasformate di Fourier, descritte dalla formula che è possibile leggere nell'immagine di apertura, purtroppo tutt'altro che facile da comprendere ed utilizzare per chi ha conoscenze matematiche elementari.

La trasformata di Fourier permette di cambiare la rappresentazione di un qualunque segnale dal dominio del tempo al dominio delle frequenze. Pur essendo uno strumento matematico diverso, può essere considerata un'estensione delle Serie di Fourier.

Dal punto di vista grafico la differenza fondamentale è che lo spettro di un segnale non periodico appare come una superficie piena. A livello intuitivo possiamo pensare che:

Un segnale non periodico non si ripete mai. Possiamo anche immaginare che il segnale si ripete con un "periodo" T molto-molto grande
La "frequenza" (f₀ = 1 / T) di un segnale non periodico è quindi molto-molto piccola
La frequenza delle armoniche, multiple intere di f₀ sono quindi molto-molto vicine tra di loro
Linee molto-molto vicine non sono distinguibili tra di loro, formano cioè una superficie

L'impulso rettangolare

L'impulso rettangolare è un segnale non periodico: la tensione ha un valore alto per un certo tempo T_ONe successivamente vale 0 V. Tale segnale non è evidentemente periodico.

Per disegnare il suo spettro partiamo dal quello dell'onda rettangolare.

Possiamo immaginare che, nella parte destra del grafico, molto lontano dall'origine e troppo a destra per essere disegnato, ci sia un altro impulso, e poi un altro ancora alla stessa distanza, e così via. Tale segnale:

ha nel dominio del tempo lo stesso grafico dell'impulso, nel senso che la parte restante non può essere disegnata perché troppo lontana dall'asse verticale
è quindi, a suo modo, periodico con un periodo molto grande; possiamo anche dire che è un segnale rettangolare con Duty Cycle molto piccolo
la sua frequenza (f = 1/T) è molto piccola; lo spettro dell'impulso sarà quindi formato da linee verticali molto vicine, in pratica una superficie
l'inviluppo è lo stesso del segnale rettangolare; esso si annulla in corrispondenza di 1/T_ON e suoi multipli interi.

Esempio 1

Consideriamo un segnale rettangolare con f = 5 kHz e T_ON = 0,02 ms. Di seguito la sua rappresentazione nel dominio del tempo e della frequenza (nota 2), grafici già visti:

Segnale rettangolare nel dominio del tempo

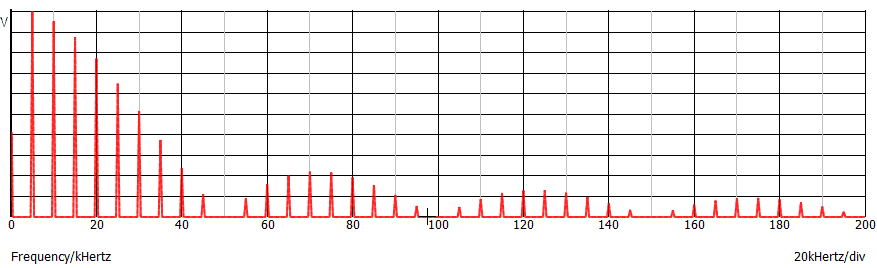
Spettro di un segnale rettangolare

Consideriamo ora un segnale rettangolare con f = 2 kHz e T_ON = 0,02 ms, lo stesso del precedente segnale. Di seguito la sua rappresentazione nel dominio del tempo e della frequenza (nota 2), grafici già visti:

Segnale rettangolare nel dominio del tempo

Spettro di un segnale rettangolare

Rispetto al caso precedente abbiamo una diminuzione della distanza tra le linee spettrali a causa della diminuzione della frequenza da 5 kHz a 2 kHz. L'inviluppo non è invece cambiato, essendo rimasto invariato T_ON.

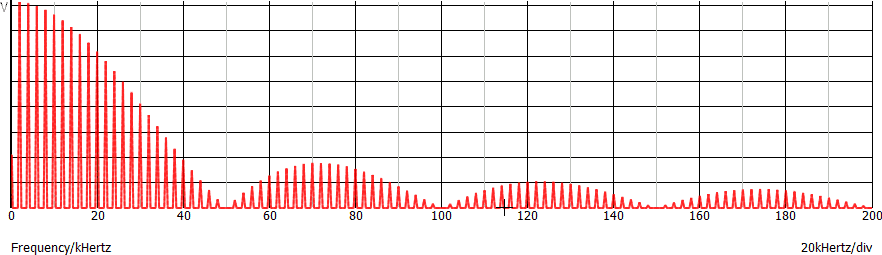
Consideriamo infine un segnale rettangolare con f = 1 kHz e T_ON = 0,02 ms. Di seguito la sua rappresentazione nel dominio del tempo e della frequenza (nota 2), grafici già visti:

Impulso nel dominio del tempo

Spettro di un segnale rettangolare

Si noti che nel grafico del dominio del tempo non solo non è possibile leggere il periodo T, ma neppure stabilire con certezza se il segnale è periodico o meno.

Rispetto al caso precedente abbiamo una ulteriore diminuzione della distanza tra le linee spettrali a causa della diminuzione della frequenza da 2 kHz a 1 kHz. L'inviluppo non è invece cambiato, essendo rimasto invariato T_ON.

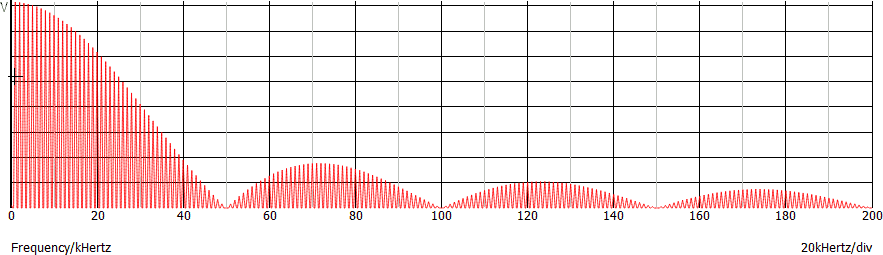
Una ulteriore diminuzione della frequenza non cambia il grafico nel dominio del tempo (perlomeno la parte mostrata). Tale segnale è spesso indicato come impulso, a volte seguito da "non periodico" oppure "singolo".

Lo spettro diventa una superficie con un andamento simile a |sin(x)/x|. Si annulla in corrispondenza di 1 / T_ON = 50 kHz (nota 2).

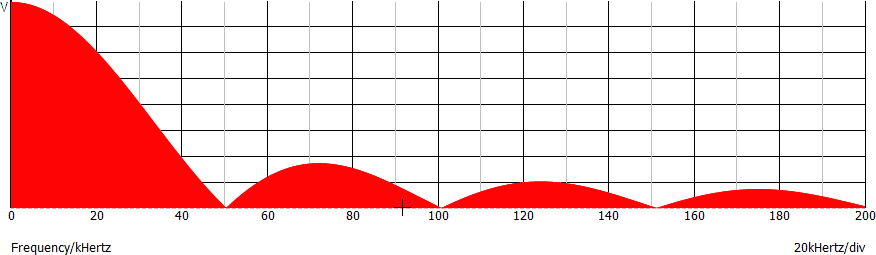
Spettro continuo dell'impulso

In genere quest'ultimo grafico viene disegnato mostrando solo il contorno, senza "colorare" la superficie.

Esercizio 2

Disegnare lo spettro di un impulso con durata 10 ms

Esempio 3

CConsideriamo una trasmissione di bit. Nel dominio del tempo appare come una sequenza di uni e zeri. Per esempio, l'immagine seguente mostra una sequenza "casuale" di bit, trasmessi alla frequenza di clock di 125 kHz. La durata di un bit è quindi Tb = 1 / 125 kHz = 8 µs.

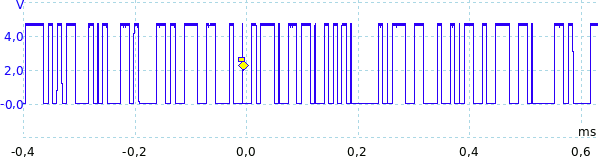
Sequenza di bit

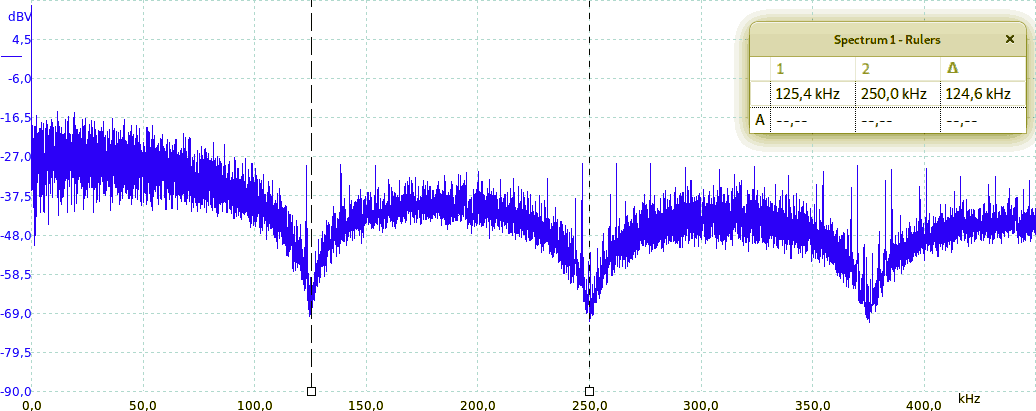
Possiamo immaginare tale sequenza come costituita da molti impulsi di durata T_ON = 8 µs. Di conseguenza lo spettro dovrà essere come sopra descritto, annullandosi a 125 kHz e multipli interi. L'immagine seguente mostra lo spettro effettivamente misurato con un analizzatore di spettro, nello specifico un Picoscope 3405A che realizza tale misura via software:

Spettro di una sequenza di bit

Esempio 4

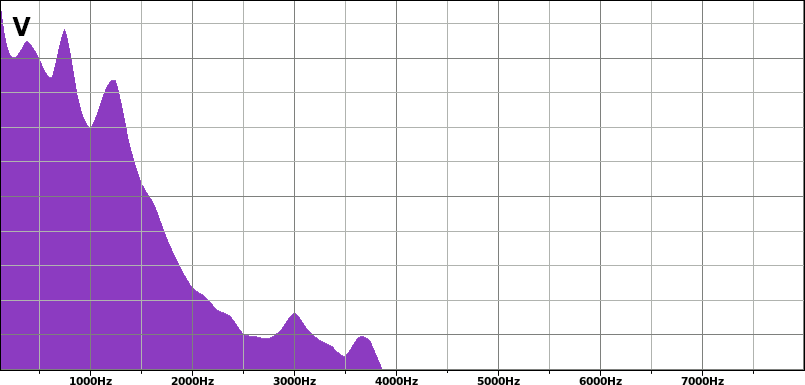
La voce umana non è periodica. Il suo spettro appare quindi come una superficie, formata da molte sinusoidi, tutte molto vicine tra di loro; la loro frequenza è compresa tra circa 0 Hz(convenzionalmente 300 Hz) e poco meno di 4 kHz (convenzionalmente 3 800 Hz)

Di seguito come appare lo spettro della voce misurato con il software Audacity (nota 1):

Spettro della voce umana

Esempio 5

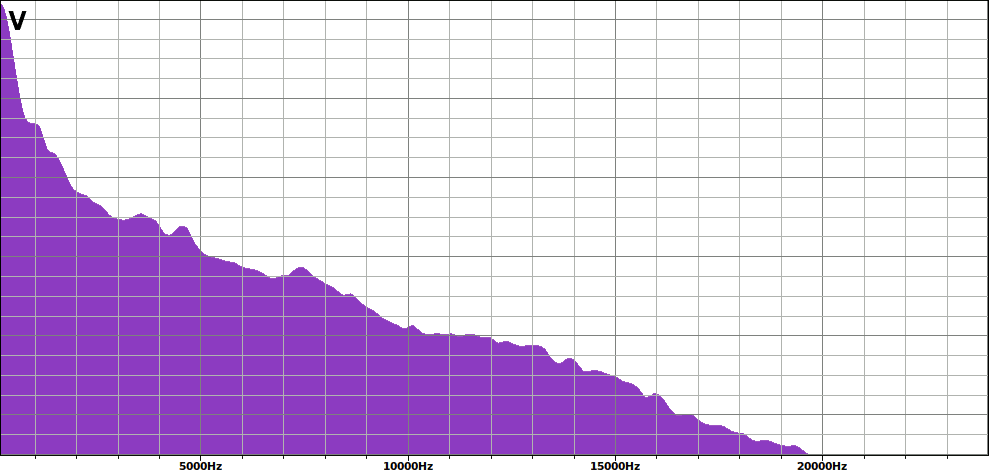
La musica contiene praticamente tutte le frequenza che l'orecchio umano può ascoltare, convenzionalmente comprese tra 30 Hz e 20 kHz.

Di seguito come appare lo spettro di un brano musicale misurato con il software Audacity (nota 1):

Spettro del segnale musicale

Banda

La banda di un segnale è l'intervallo di frequenze entro cui sono contenute tutte le linee spettrali di un segnale.

Alcuni esempi:

Il segnale audio ha convenzionalmente una banda di circa 20 kHz, compresa tra 20 Hz e 20 kHz. Queste sono le frequenza che l'orecchio umano medio è in grado di sentire
Il segnale vocale ha convenzionalmente banda compresa tra 300 Hz e 3.8 kHz. Esso contiene tutte le frequenza necessarie alla comprensione del parlato
L'impulso ed il segnale dell'esempio 3 hanno teoricamente banda infinita. In genere ci si limita però a considerare solo una parte della superficie in quanto normalmente l'ampiezza decrescere al crescere della frequenza fino a diventare trascurabile.
Una radio commerciale broadcast che trasmette in modulazione di frequenza (FM) occupa una banda di circa 180 kHz intorno ad una frequenza centrale (portante). Per esempio RTL 102.5 trasmette frequenza intorno a 102.5 MHz, occupando quindi le frequenza comprese tra circa 102.4i MHz e 102.59 MHz
L'insieme di tutte le radio commerciali broadcast che trasmettono in FM occupano la banda di 20.5 MHz, compresa tra 87,5 MHz e 108 MHz (banda VHF-II).
Il canale WiFi usato da questo apparato occupa una banda di 80 MHz, con una frequenza centrale di 5,21 GHz, occupando le frequenza tra 5 170 MHz e 5 250 MHz
L'insieme di tutti i canali WiFi a 5 GHz per usi indoor occupano una banda di 190 MHz compresa tra 5.15 GHz e 5.34 GHz (UNII-1)

Note

Quello mostrato è in realtà uno spettro logaritmico
In questa pagina non sono discusse le ampiezze perché argomento complesso da affrontare. Per questo non appaiono numeri sull'asse verticale dello spettro

Pagina creata nell'ottobre 2020
Ultima modifica: 15 settembre 2023