
Un quadripolo è una generica rete elettrica in cui sono presenti una coppia di morsetti di ingresso ed una coppia di morsetti di uscita. In ingresso è applicato un segnale elettrico: potrebbe essere una tensione (come sempre qui in seguito), una corrente, una potenza o qualunque altra grandezza. In uscita sarà presente un'altra grandezza elettrica, uguale o diversa da quella di ingresso ottenuta elaborando la grandezza in ingresso.
Questo argomento è sviluppato nelle seguenti pagine:
Nel seguito si faranno le seguenti ipotesi semplificative:
La trasformata di laplace permette di studiare una rete elettrica lineare con ingressi di qualunque tipo (e quindi non solo sinusoidali). In sé lo strumento matematico è piuttosto complesso ed anche la semplice applicazione usando tabelle non è sempre immediata.
Qui verrà però considerata come una banale modifica del metodo simbolico. In questo caso è sufficiente applicare la trasformazione:
![]()
all'impedenza di condensatori e induttori. Si ottengono quindi le seguenti impedenze:
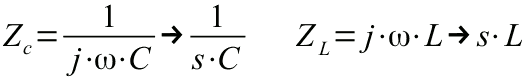
Successivamente verranno applicate le leggi e i metodi tipici dell'elettrotecnica
La funzione di trasferimento è una funzione che indica il rapporto tra la grandezza di uscita e la grandezza di ingresso di un quadripolo; la definizione è analoga a quella di quadagno. Nelle ipotesi semplificative qui utilizzate è definita come:
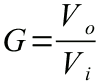
Dove Vo e Vi sono la tensione di uscita e di ingresso. Nel caso semplificato in esame G è adimensionale (numero puro).
Se il calcolo viene eseguito usando le trasformate di Laplace, la funzione di trasferimento viene spesso indicata con G(s). Ricordando la definizione di s, la funzione di trasferimento è un numero complesso quindi dotato di modulo e fase (o anche: parte reale e parte immaginaria).
Spesso il modulo della funzione di trasferimento viene chiamato guadagno del quadripolo:
Se consideri un partitore di tensione costituito da un resistore in serie ad un condensatore. Sia Vo la tensione ai capi del condensatore.
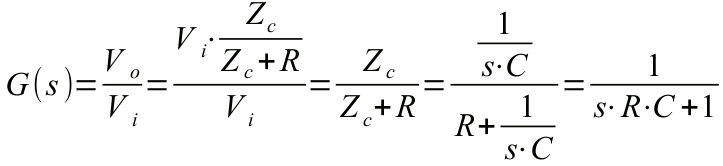
Più in generale, nello condizioni semplificate qui utilizzate, la funzione di trasferimento è costituita da una frazione in cui sia il numeratore che il denominatore sono polinomi in s. Di seguito due forme spesso usate, dove a, b, c, A, B ... sono costanti numeriche qualunque, anche nulle:
La prima forma è più generale, la seconda è limitata al solo caso in cui tutte le radici sono reali.
Il teorema fondamentale dell'algebra afferma che il numero di radici di un polinomio, reali o complesse, contate con la loro molteplicità, coincide con il grado del polinomio stesso.
Si definisce:
A volte poli e zeri sono chiamati anche punti di rottura a causa del fatto che il grafico del modulo è costituito in prima approssimazione da una spezzate che ha i propri vertici in corrispondenza di questi punti.
Esempio: nella G(s) sopra calcolata abbiamo un solo polo (di valore -1/RC) e nessuno zero
Osservazioni conclusive:
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)