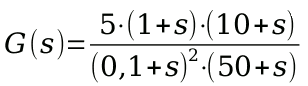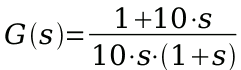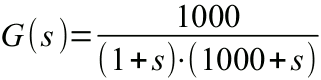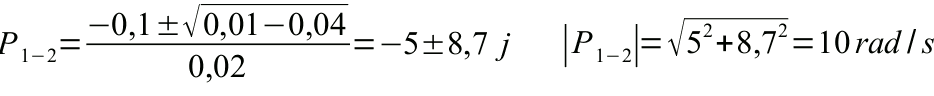Home → Tutorial →
Appunti scolastici → Quadripoli → Funzione di
trasferimento → Diagrammi di Bode asintotici
I diagrammi di bode sono grafici che descrivono come varia il modulo e la
fase di una funzione di trasferimento al variare della frequenza. Di seguito verrà illustrato con qualche esempio il tracciamento
asintotico, cioè approssimato usando segmenti di rette.
Spesso il diagramma di bode è indicato anche col termine risposta in
frequenza in quanto rappresenta come la risposta (cioè l'uscita) di un
circuito cambia con la frequenza
I vari paragrafi
illustrano situazioni via-via più complesse e quindi è opportuno leggere la
pagina nell'ordine proposto.
La griglia da utilizzare è riportata nella pagina
Unità logaritmiche - Griglia per i
diagramma di Bode:
- In orizzontale vanno riportati i valori di s in radianti al secondo
(come negli esempi seguenti) oppure Hz, su scala logaritmica
- In verticale il modulo del guadagno (in dB, in genere una divisione
corrisponde a 20 dB) oppure la fase
(in °, in genere una divisione corrisponde a 90°)
Un diagramma di bode asintotico è costituito, nella versione semplificata qui
descritta, esclusivamente da:
- Segmenti orizzontali
- Segmenti "in salita" inclinati di +20 dB/decade cioè paralleli ad
una retta passante per i vertici delle divisioni principali della
griglia (le linee continue, non quelle tratteggiate)
- Segmenti inclinati di + 40 dB/decade, 60 dB/decade e multipli interi
- Segmenti "in discesa" inclinati di -20 dB/decade e suoi multipli
interi
Spesso la pendenza di +20 dB/decade viene indicata come +1; la pendenza
di -40 dB/decade viene indicata come -2; un segmento orizzontale con
pendenza 0.
Caso 1 - Poli e zeri reali, minori di zero - Modulo
Le regole per tracciare il modulo del diagramma di bode sono le seguenti:
- Trovare poli e zeri, calcolare il loro modulo e ordinarli in
modo crescente
- Il grafico inizia orizzontalmente da sinistra (in realtà il temine
"iniziare" non è corretto: il grafico si estende verso sinistra
all'infinito). Il
valore si può calcolare ponendo s = 0. E' corretto anche
assegnare ad s un altro valore purché molto più
piccolo di qualunque zero o polo presente
- Ci spostiamo verso destra, fino ad incontrare un polo: la pendenza,
da questo valore di s in poi, diminuisce di 20 dB/decade
(cioè cambia di -1)
- Se si incontra uno zero, la pendenza aumenta di 20 dB/decade (cioè
di +1)
- Se incontriamo coppie di poli o zeri coincidenti (in gergo: doppi),
la variazione di pendenza raddoppia
Nota importante: dire che la pendenza aumenta è diverso
dal dire che il valore aumenta!
Per una verifica (parziale) del risultato possiamo osservare che la
pendenza "finale" è pari al numero degli zeri meno il numero dei poli.
Vediamo un esempio:
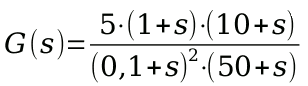
Questa funzione di trasferimento presenta due zeri e tre poli, tutti
negativi. Calcoliamoli e scriviamoli in ordine, secondo il valore del loro modulo, dal
più piccolo al più grande:
- polo per s = -0,1, doppio (è elevato al quadrato!)
- zero per s = -1
- zero per s = -10
- polo per s = -50
Calcoliamo il valore "iniziale" in dB, ponendo s = 0 nella G(s). In alternativa,
con lo stesso risultato,
poteva essere usato un qualunque valore di s molto più piccolo
del polo o dello zero più piccolo, approssimando poi il risultato:
G(0) = 100 = 40 dB
- Scriviamo sul diagramma di bode i seguenti valori, cercando di
occupare la parte centrale della griglia:
- modulo dei poli, sull'asse delle ascisse
- modulo degli zeri, sull'asse delle ascisse
- il valore "iniziale" di G(0) sopra calcolato e qualche valore al
di sopra o al di sotto, sull'asse delle ordinate
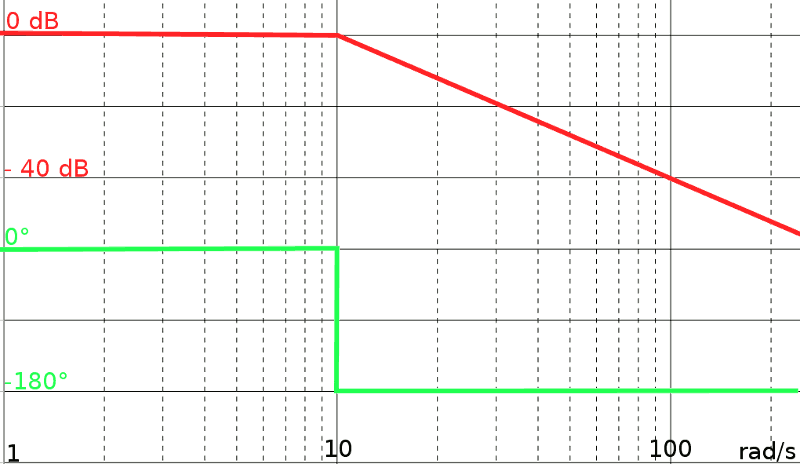
- Tracciamo una linea orizzontale dall'estrema sinistra della griglia
fino al valore del modulo del primo polo o zero. Tale linea verso
sinistra prosegue illimitatamente. In verde nel grafico
- Arrivati a 0,1 rad/s troviamo un polo doppio: la pendenza cambia di -2
e passa da 0 a -2 (-40 dB/decade, cioè nell'intervallo tra 0,1 e 1
diminuisce di 40 dB). Tratto blu
- Arrivati a 1 troviamo uno zero. La pendenza aumenta di 1e passa da -2 a -1. Tratto fucsia
- Arrivati a 10 troviamo un altro zero. La pendenza aumenta di 1 e passa da -1 a 0. Tratto giallo
- Arrivati a 50 troviamo l'ultimo polo. La pendenza cambia di -1
e passa da 0 a -1. Tratto arancione. Tale tratto prosegue
illimitatamente senza variazioni di pendenza
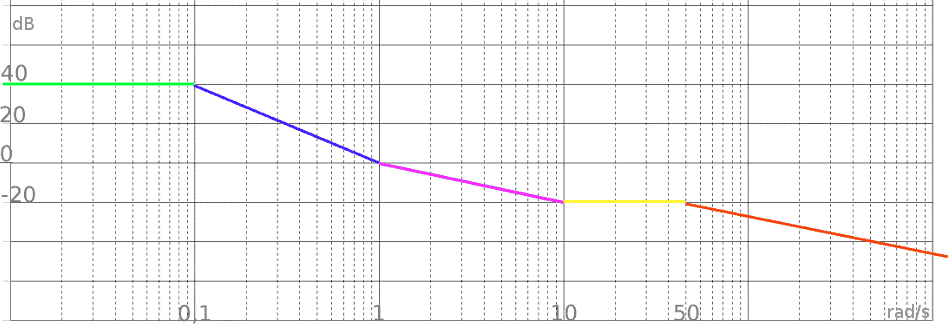
Si noti che i tratti fucsia e arancione sono tra loro paralleli, cosa
ovvia osservando che entrambi hanno pendenza -20 dB/decade.
Si noti inoltre che la pendenza finale poteva essere facilmente prevista
osservando che siamo in presenza di 3 poli e due zeri (2 - 3 = -1)
Caso 1bis - Poli e zeri reali, minori di zero - Fase "a gradini"
Le regole per tracciare il diagramma della fase sono le seguenti:
- Trovati poli e zeri, occorre calcolare il loro modulo e ordinarli in
modo crescente. E' lo stesso passaggio del punto precedente
- Il grafico inizia orizzontale a sinistra del grafico. Il valore
iniziale è zero
- Se si incontra un polo, la fase diminuisce "a gradino" di 90°. Questa regola è
molto approssimata!
- Se si incontra uno zero, la fase aumenta di 90°. Questa regola è
molto approssimata!
Nota importante: dire che la fase aumenta è diverso dal
dire che la pendenza aumenta!
Applichiamo queste regole allo stesso esempio di cui sopra:

Caso 2 - Poli o zeri nell'origine
Un polo (o uno zero) si dice nell'origine se ha valore zero.
Il procedimento è simile ai precedenti con le seguenti aggiunte:
- Se è presente un polo nell'origine, il grafico del modulo "inizia" già
inclinato di -1
- Se è presente uno zero nell'origine, il grafico del modulo "inizia"
già inclinato di +1
- Se è presente un polo nell'origine, il grafico della fase "inizia" da
-90°
- Se è presente uno zero nell'origine, il grafico della fase "inizia" da
+90°
- Se sono presenti due o più poli o zeri nell'origine l'inclinazione iniziale del
grafico del modulo è ±2, ±3 ecc.
- Se sono presenti due o più poli o zeri nell'origine la fase iniziale vale
±180° e multipli di 90°
Vediamo un esempio:
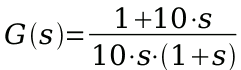
Questa funzione di trasferimento presenta uno zero e due poli. Calcoliamoli e scriviamoli ordinandoli secondo il loro modulo, dal
più piccolo al più grande in modulo:
- polo per s = 0 (nell'origine)
- zero per s = -0,1
- polo per s = -1
Come sempre in questi casi, non possiamo calcolare la G(0) in quanto risulta una forma indeterminata
(∞). Calcoliamo quindi, per esempio, la G(s) per un
valore di s pari a 0,001, molto più piccolo di 0,1:
G(0,001) = 100 = 40 dB
- Scriviamo sul diagramma di bode i seguenti valori, cercando di
occupare la parte centrale della griglia:
- modulo del polo diverso
da 0
- modulo dello zero
- valore di s utilizzato nella formula sopra riportata
- valore del guadagno un corrispondenza del valore di s sopra
scelto
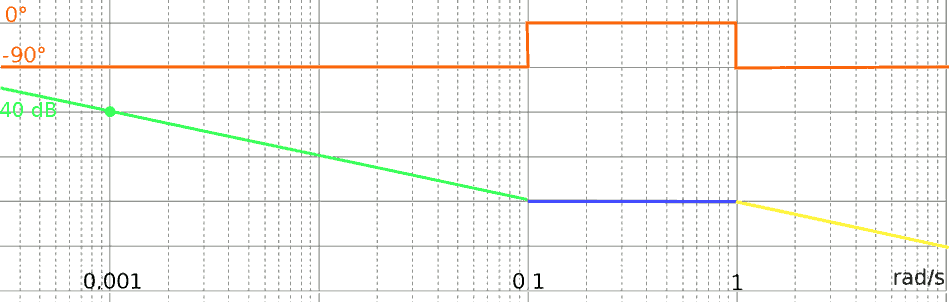
- Abbiamo un polo nell'origine: il grafico parte già inclinato di -1.
Tale retta deve passare per il punto (0.001; 40), sopra calcolato.
Verso sinistra, al di fuori del grafico, il grafico continua a salire.
In verde
- A 0,1 troviamo uno zero, la pendenza passa da -1 a 0. In blu
- A 1 troviamo un polo, la pendenza diventa -1. In giallo
- La fase inizia da -90°; a 0,1 passa a 0°; a 1 torna definitivamente
a -90°. In arancione, disegnata sullo stesso grafico del modulo, come in
genere si preferisce fare
Approssimiamo meglio la fase
Come detto, il disegno "a gradini" della fase ha una precisione molto
bassa.
Per meglio approssimare il grafico possiamo aggiungere la seguente
regola:
- Dato un polo (o uno zero) individuare il punto del grafico a gradini
una decade prima e una decade dopo
- Unire questi punti con un segmento
Vediamo un primo esempio, con due poli piuttosto lontani tra di loro.
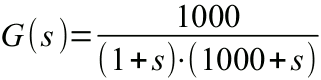
Oltre al modulo (in verde) è riportato il grafico della fase "a gradini"
(in giallo) e quello meglio approssimato (in blu).
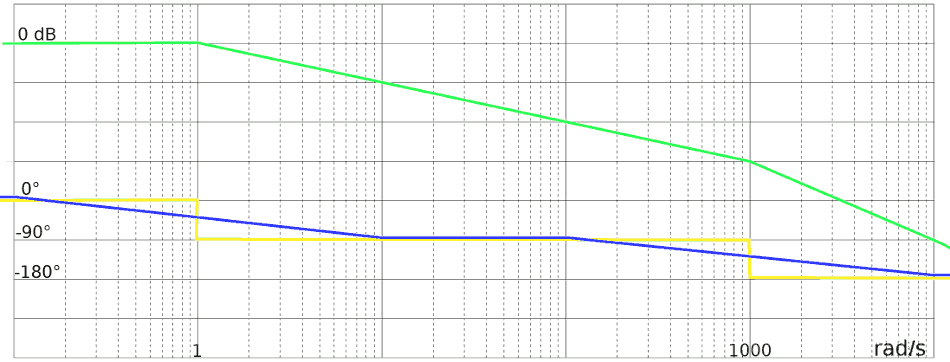
Osservazioni:
- Il grafico della fase prosegue a sinistra orizzontalmente
- Il grafico della fase prosegue a destra orizzontalmente
- In zone molto lontane dai poli (o dagli zeri) i due grafici della
fase coincidono: nell'esempio tra 10 e 100 rad/s oppure per valori
inferiori a 0,1 rad/s
- In corrispondenza dei poli (o degli zeri) i due grafici della fase
coincidono. In questi punti la fase vale esattamente 45° oppure 135° (90°
+ 45°)
Poli e zeri positivi
Occorre preliminarmente precisare che questo caso non si verifica mai nei
sistemi costituiti da soli componenti RLC. Potrebbero invece essere presenti
in sistemi retroazionati, più complessi.
Per quanto riguarda il grafico del modulo non cambia nulla rispetto a quanto già detto.
Per quanto riguarda la fase il comportamento è esattamente il contrario di
quanto descritto:
- Un polo positivo fa aumentare la fase di +90°
- Uno zero positivo cambia la fase di -90°
Le soluzioni di un'equazione di grado n sono sempre presenti n radici,
alcune reale e altre complesse e coniugate, cioè coppie di soluzioni con
parte reale coincidente e parte immaginaria cambiata di segno.
Se si considerano i soli grafici asintotici nulla cambia rispetto a
quanto già descritto, avendo la sola avvertenza di considerare il modulo di
poli e zeri. Per quanto riguarda la fase, il segno da considerare è quello
della parte reale (in genere negativa). Evidentemente questi poli e questi zeri sono sempre doppi.
Vediamo un esempio:
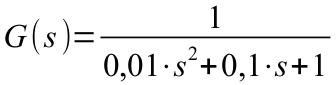
Troviamo i due poli. Il determinante è negativo e quindi è presente una
parte immaginaria.
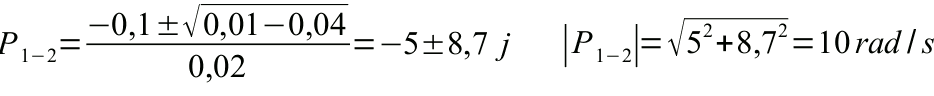
Il diagramma asintotico di bode, modulo e fase, è quindi il seguente: