Questa pagina descrive cosa è un segnale campionato e come la corrispondente operazione di campionamento influisce sul segnale, sia nel dominio del tempo che nel dominio della frequenza.
Per elaborare numericamente un segnale variabile occorre trasformarlo in un insieme di numeri attraverso l'operazione di digitalizzazione. L'hardware utilizzato è il Convertitore Analogico Digitale (ADC).
Le operazioni effettuate per digitalizzare un segnale analogico variabile nel tempo sono due, concettualmente indipendenti:
In questa pagina si affronterà solo il primo di questi due aspetti.
Campionare un segnale significa prelevare il valore del segnale stesso ad intervalli regolari di tempo.
Due esempi dalla vita di tutti i giorni:
Il problema fondamentale è scegliere correttamente l'intervallo di tempo da usare per effettuare le misure:
Un esempio più tecnico, relativo ad un segnale sinusoidale:
Possiamo dire che il segnale campionato ha valore pari a quello del segnale originale negli istanti di campionamento ed è indefinito negli altri istanti di tempo; di seguito una rappresentazione grafica del solo segnale campionato:
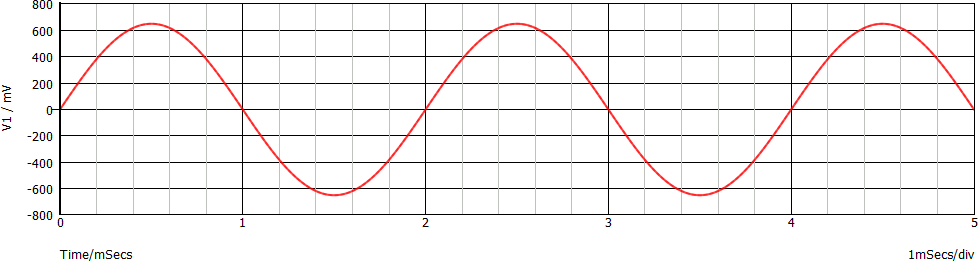
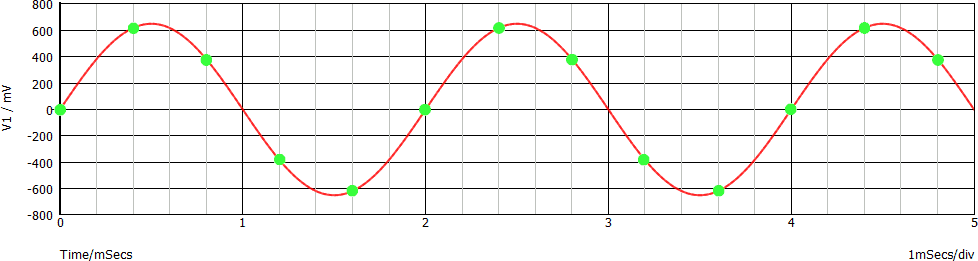
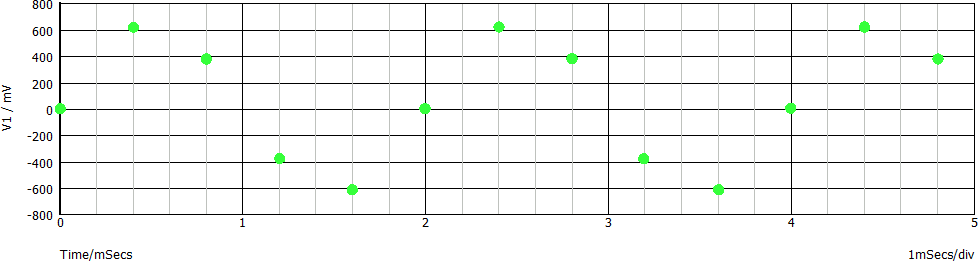
Andiamo oltre: dimezziamo la frequenza di campionamento (fc = 1,25 ksps). Di seguito il grafico corrispondente, relativo al solo segnale campionato:
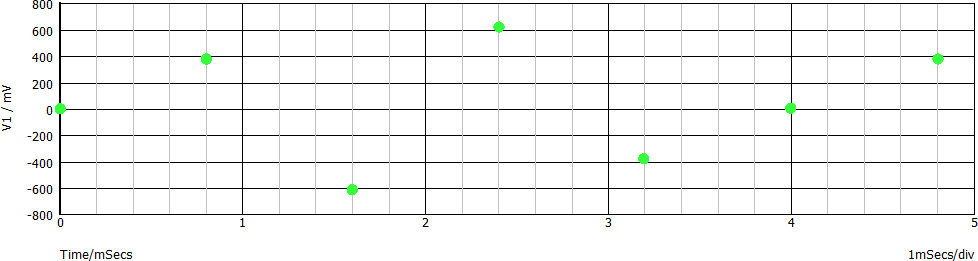
Domanda: in riferimento ai due esempi appena mostrati, possiamo ricostruire esattamente il segnale sinusoidale originale (rosso) a partire dal segnale campionato (verde)?
La risposta corretta è poco intuitiva ed è affermativa in entrambi i casi; è data dal teorema del campionamento (o di Nyquist o di Shannon o di Whittaker-Nyquist-Kotelnikov-Shannon).
Enunciato: per campionare correttamente un segnale s è necessario utilizzare un frequenza di campionamento fc pari ad almeno il doppio della massima frequenza presente nello spettro di s.
Nei due casi esposti, il segnale ha frequenza massima pari a 500 Hz. Le due frequenze di campionamento usate nei due esempi sono rispettivamente 2,5 ksps (migliaia di samples per second, cioè migliaia di campioni al secondo) e 1,25 ksps. Le condizioni del teorema sono quindi soddisfatte.
Questo teorema ha ripercussioni importanti a livello applicativo:
Alcuni esempi:
Se non è rispettata la frequenza minima di campionamento richiesta dal teorema del campionamento, il segnale campionato diventa assolutamente diverso da quello originale (aliasing).
Quale frequenza di campionamento occorre utilizzare, come minimo, per campionare:
Per comprendere, almeno in parte, l'origine del teorema del campionamento occorre analizzare lo spettro del segnale campionato in funzione dello spettro del segnale originale e della frequenza di campionamento.
In sintesi, e senza alcun tentativo di dimostrazione, possiamo dire che lo spettro del segnale campionato alla frequenza fc è formato da:
Ignoriamo in questa trattazione semplificata ogni riferimento all'ampiezza di queste linee spettrali.
Consideriamo il segnale utilizzato nell'esempio 1, campionato alla frequenza di 2,5 ksps. Lo spettro del segnale di ingresso è facile da disegnare, trattandosi di una sinusoide:
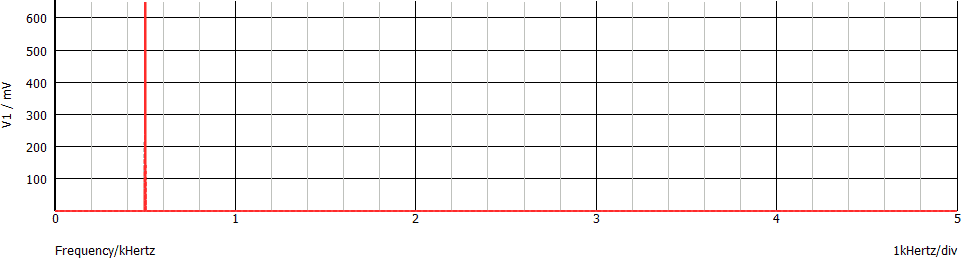
La frequenza di campionamento utilizzata nell'esempio 1 è pari a 2.5 ksps. Lo spettro campionato conterrà quindi:
Graficamente:
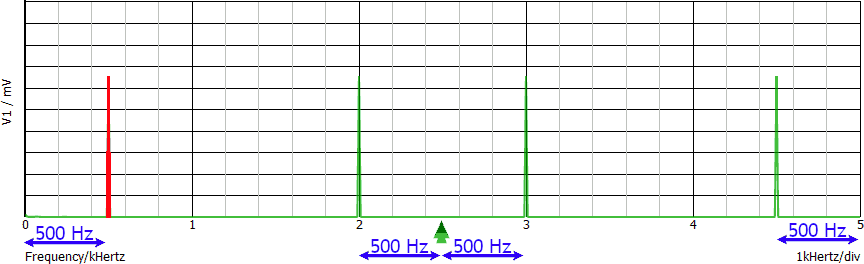
La freccia verde indica la frequenza di campionamento (2.5 ksps). Sono stati omessi i numeri lungo l'asse verticale per non introdurre un ulteriore livello di complicazione.
Se dal grafico elimino tutte le linee spettrali incluse nella fascia grigia (oltre la metà della frequenza di campionamento) ottengo esattamente il segnale di partenza:
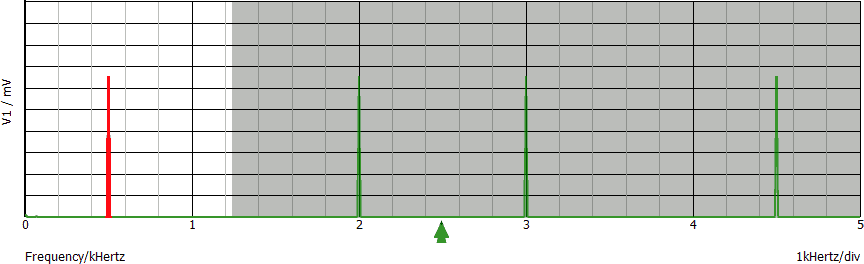
Consideriamo ancora il segnale utilizzato nell'esempio 1, campionato questa volta alla frequenza di 1,25 ksps (esempio 1bis). Lo spettro del segnale di ingresso lo abbiamo appena disegnato:
La frequenza di campionamento utilizzata nell'esempio 1bis è pari a 1.25 ksps. Lo spettro campionato conterrà quindi:
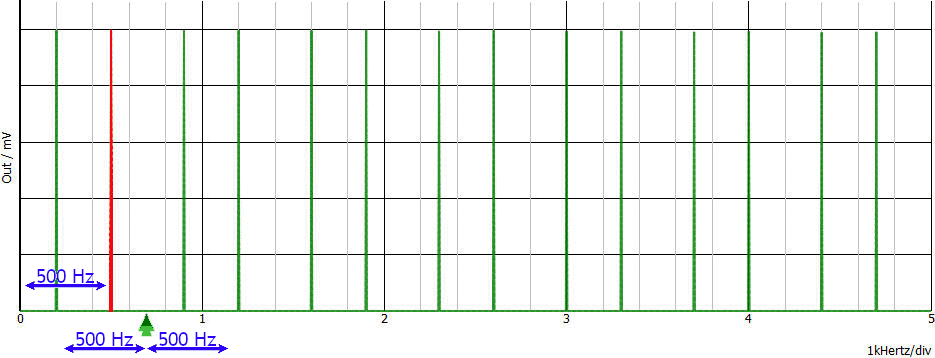
Graficamente:
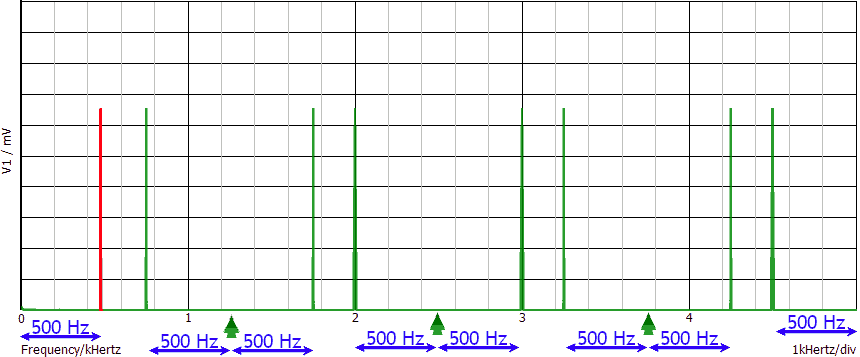
La freccia verde indica la frequenza di campionamento (1.25 ksps). Sono stati omessi i numeri lungo l'asse verticale per non introdurre un ulteriore livello di complicazione.
Se dal grafico elimino tutte le linee spettrali incluse nella fascia grigia (oltre la metà della frequenza di campionamento) ottengo esattamente il segnale di partenza:
Consideriamo ancora il segnale utilizzato nell'esempio 1, con frequenza 500 Hz, campionato questa volta alla frequenza di 700 sps, quindi ad una frequenza inferiore al minimo richiesto dal teorema del campionamento. Lo spettro del segnale di ingresso lo abbiamo già disegnato:
La frequenza di campionamento utilizzata è pari a 0,7 ksps. Lo spettro campionato conterrà quindi:
Graficamente:
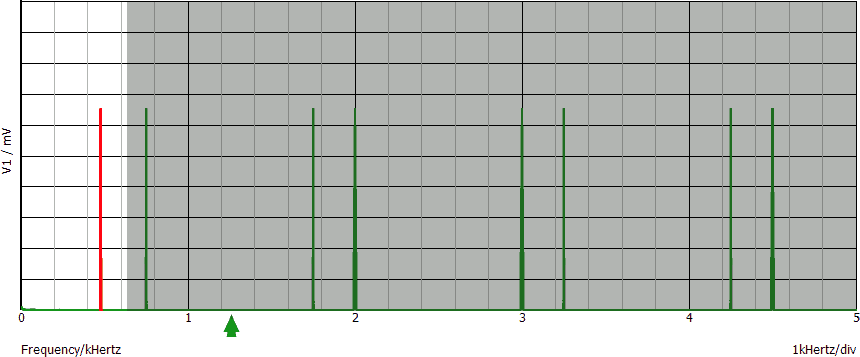
La freccia verde indica la frequenza di campionamento (700 sps). Sono stati omessi i numeri lungo l'asse verticale per non introdurre un ulteriore livello di complicazione.
Se dal grafico elimino tutte le linee spettrali incluse nella fascia grigia (oltre la metà della frequenza di campionamento) non solo non ottengo il segnale di partenza, ma appare una linea spettrale inesistente nel segnale originale, alla frequenza di 200 Hz:
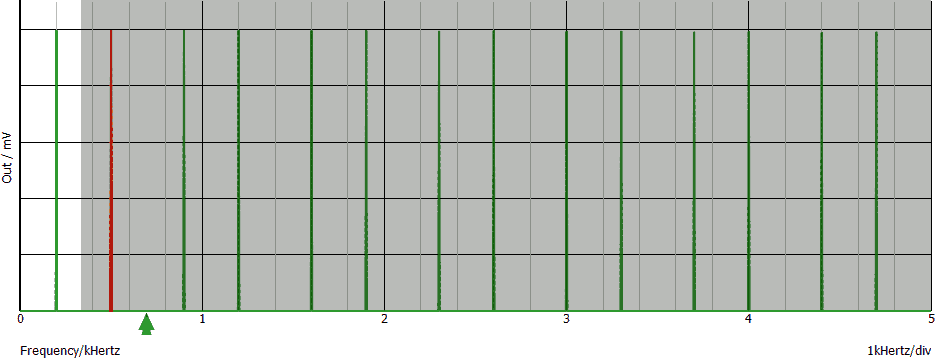
Tale fenomeno è chiamato aliasing.
Un segnale ha lo spettro seguente:
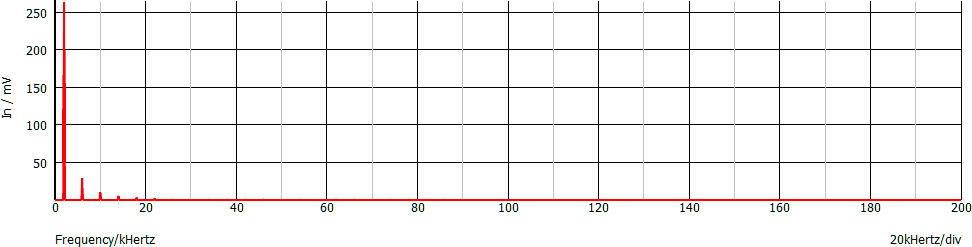
Con una certa approssimazione possiamo dire che la sua frequenza è 2 kHz (fondamentale) e che contiene armoniche con frequenza 6 kHz, 10 kHz, 14 kHz, 18 kHz, 22 kHz (e forse altre di ampiezza molto piccola).
Esso viene campionato alla frequenza di campionamento fc = 100 ksps. Di seguito lo spettro del segnale campionato, ottenuto con un programma di simulazione.
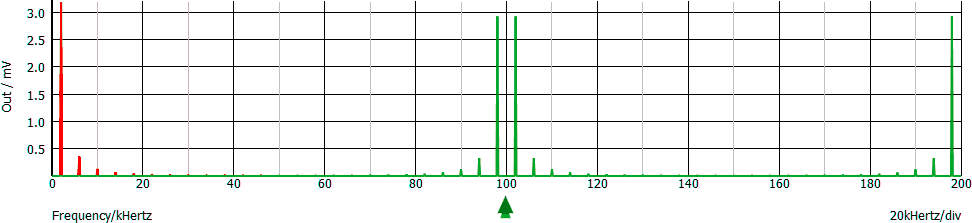
Leggiamo il grafico, confrontandolo con quello del segnale originale:
Eliminando tutte le linee spettrali maggiori di metà della frequenza di campionamento
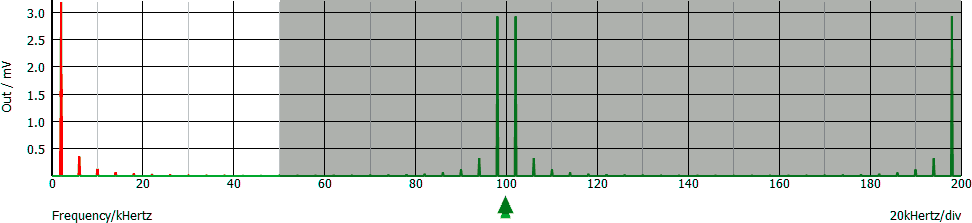
Un segnale ha il seguente spettro:
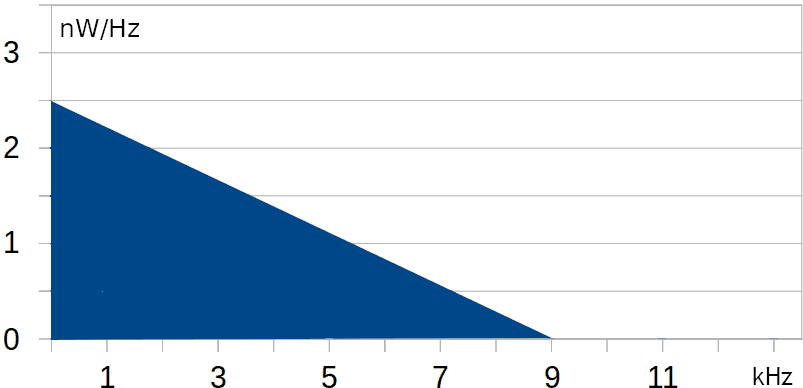
Questo segnale è non periodico e quindi "non ha" una frequenza: infatti lo spettro è una superficie e non un insieme di linee verticali multiple della fondamentale
La massima frequenza contenuta nel segnale è 9 kHz e quindi la frequenza di campionamento deve essere maggiore di 18 kHz
Possiamo per esempio scegliere come frequenza di campionamento 20 kHz (> 18 kHz). Di seguito lo spettro del segnale campionato:
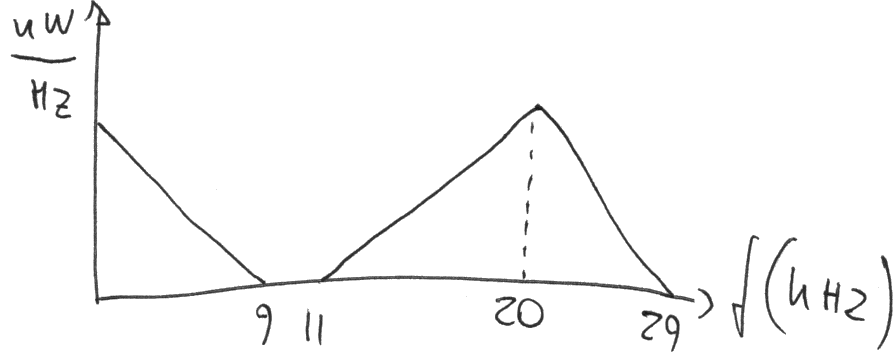
Due osservazioni:
Pagina creata nel maggio 2023
Ultima modifica:
6 aprile 2024
L'immagine di apertura è relativa alla formazione del Padova che ha partecipato al campionato di calcio 1922/23. Immagine di pubblico dominio.
Appunti scolastici - Versione 0.1031 - Marzo 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)
