

Il rumore elettronico (N, noise) è un segnale indesiderato che si somma al segnale utile (S, signal), degradandolo. Il rumore è presente in qualunque circuito elettronico, indipendentemente dalla presenza di altri segnali.
Un errore grave, sintomo di non comprensione dell'argomento: confondere la distorsione con il rumore.
Il rumore è classificabile in base alla sua causa e, di conseguenza, alle tecniche per ridurlo:
Questo rumore è, come dice il nome, generato al di fuori dell'apparecchiatura che trasmette o riceve un segnale.
Può essere di origine naturale (fulmine, tempesta solare...) oppure artificiale (linea per la trasmissione dati, trasmettitore radio, impianto elettrico, alimentatore switching...). Spesso è indicato con il termine interferenza, soprattutto se artificiale.
Per ridurre gli effetti negativi delle interferenze è possibile usare vari accorgimenti:
Le attività necessarie per analizzare e ridurre le interferenze generate e aumentare la resistenza alle interferenze vengono affrontati nei processo di esame della compatibilità elettromagnetica, obbligatorio per ottenere la certificazione CE.
Come dice il nome, questo rumore è generato all'interno dell'apparecchiatura che trasmette o riceve un segnale e non può quindi essere da essa separato, schermato o allontanato. Esso non è eliminabile e rende complesso il buon funzionamento di un circuito o di sistema di comunicazione.
Questo rumore è legato principalmente due (nota 2) fenomeni, tra loro indipendenti:
Le caratteristiche del rumore termico:
Le caratteristiche del rumore granulare sono molto simili a quelle del rumore termico, tranne:
In molte situazioni il rumore granulare è trascurabile rispetto a quello termico: operativamente, per tener conto di entrambi i contributi con un solo numero, si considera una temperatura di rumore un po' superiore a quella fisica (nota 1).
Per ridurne, non annullare, gli effetti negativi del rumore interno è possibile usare vari accorgimenti:
Il seguente esempio mostra un segnale sinusoidale (30 mV di picco, 100 kHz) a cui è sommato un rumore di origine interna, con andamento casuale. La banda dell'oscilloscopio utilizzato nella misura è 100 MHz cioè capace di mostrare tutti i segnali e tutto il rumore che che ricadono nell'intervallo di frequenze da 0 Hz a 100 MHz.
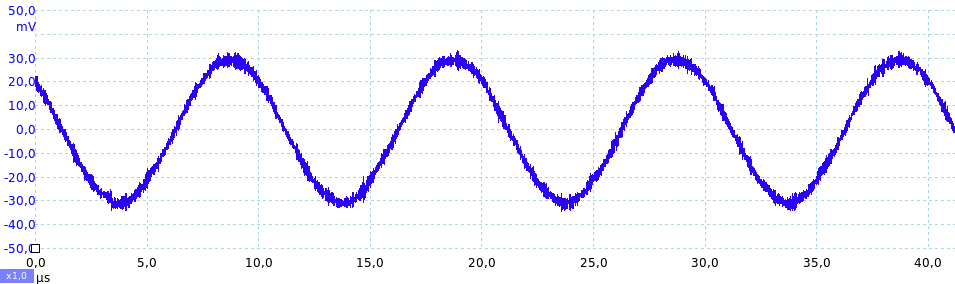
Lo spettro seguente mostra con una scala logaritmica lo spettro di potenza dello stesso segnale descritto al punto precedente:
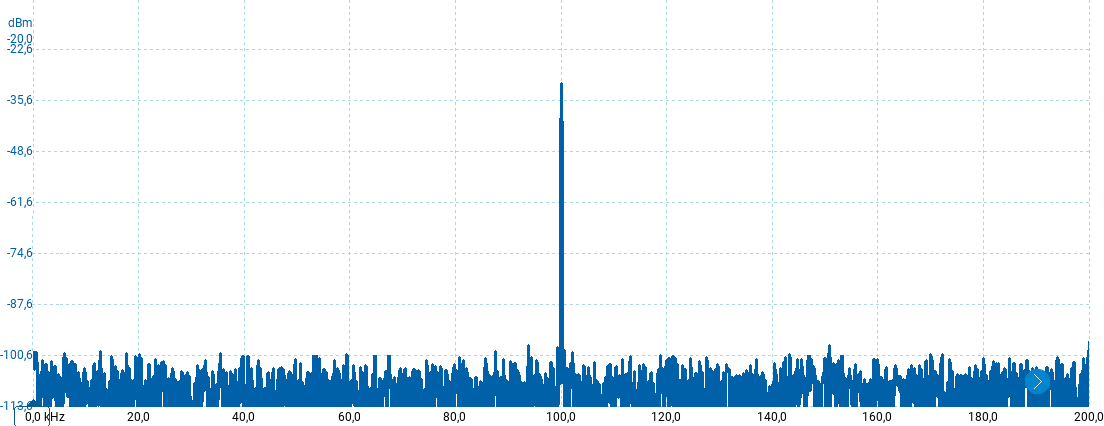
Si può osservare:
Da questa figura si intuisce che:
Di seguito lo stesso segnale dei punti precedenti visto con un oscilloscopio con banda 20 MHz: il segnale è invariato in quanto inferiore a 20 MHz; il rumore totale è diminuito in quanto il rumore compreso tra 20 MHz e 100 MHz non è stato misurato.
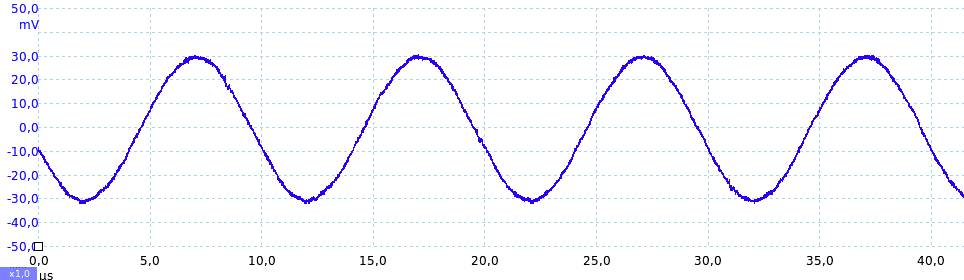
La seguente immagine mostra una fotografia in cui è presente nella metà di destra un rumore significativo, fenomeno tipico delle riprese notturne; l'immagine, oltre che ovviamente più scura, è fortemente degradata dalla presenza di pixel dai colori casualmente modificati.

In un sistema analogico audio il rumore termico di manifesta come fruscio.
In un sistema digitale il rumore, se piccolo, non ha effetti: un livello logico alto rimane alto ed un livello logico basso rimane basso:
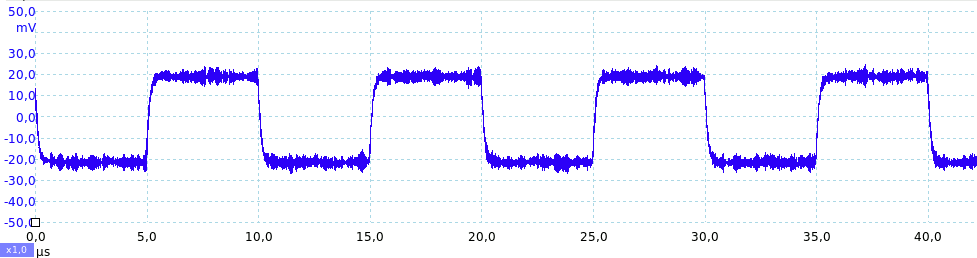
Se il rumore è invece ampio, un bit potrebbe cambiare valore: è intuitivo immaginare che, maggiore è il rumore, maggiore sarà la probabilità di avere bit errati. Il tasso di errori in genere viene indicato come BER (Bit Error Rate), definito come rapporto tra il numero di bit errati ed il numero totale di bit. Valori ragionevoli di BER vanno da 10-3 (telefonia di vecchio tipo) a 10-12 (Ethernet).
La potenza del rumore termico può essere qualitativamente valutata a partire dalle caratteristiche del precedente elenco.
Una formula spesso usata calcola tale potenza in unità logaritmiche come:
N(dBm) = 10 · log(1,38 · T(k)) + 10 · log( B(Hz) ) - 200
Dove:
Se vogliamo misurare il solo rumore di origine termica, la temperatura utilizzata nella formula è quella quella fisica, misurata con un normale termometro.
Se vogliamo misurare tutto il rumore di origine interna viene introdotto il concetto di temperatura di rumore, più alta di quella fisica e che include anche gli effetti del rumore interno di origine non termica (nota 1). Questa grandezza non corrisponde a nulla di fisicamente definibile, ma è la "T" ottenuto dalla formula inversa di quella sopra riportata.
Utile vedere l'esempio 1 ed i successivi esercizi.
Il danno causato dal rumore non dipende tanto dal suo valore assoluto, quanto dal rapporto tra la potenza del segnale utile (S oppure RSSI, Received Signal Strength Indicator) e la potenza del rumore (N). Tale rapporto è in genere è indicato come SNR (Signal to Noise Ratio).
A volte, raramente a livello applicativo, è espresso come numero puro (adimensionale, cioè senza unità di misura), utilizzando la formula ottenuta direttamente dalla definizione:
SNR = S(W) / N(W)
Più spesso il SNR è espresso in unità logaritmiche, utilizzando la formula seguente che, per le proprietà dei logaritmi, trasforma una divisione in una differenza:
SNR(dB) = S(dBm) - N(dBm)
Si noti che SNR, essendo un numero puro, in unità logaritmiche è espresso in dB. Le potenze sono invece espresse in dBm.
Tale valore non deve essere troppo piccolo al fine di permettere un corretta funzionamento delle apparecchiature. In genere sono richiesti SNR di alcune decine di decibel, ma esistono particolari tecniche di modulazione che sono in grado di funzionare correttamente anche con SNR minori di zero, cioè con un segnale minore del rumore.
Alcune osservazioni importanti:
Utile vedere l'esempio 2 ed i successivi esercizi.
L'importanza del SNR nelle trasmissioni digitali deriva dal teorema di Shannon-Hartley: la massima velocità teorica di un canale di comunicazione digitale è data da:
C(bit/s) = B(Hz) · log2 (1 + SNR) (nota 6)
Se SNR è elevato (come spesso è) è possibile utilizzare una formula approssimata, più comoda a livello applicativo, esprimendo SNR direttamente in unità logaritmiche:
C(bit/s) ≈ B(Hz) · SNR(dB) / 3
Tali formule sono ottenute da una dimostrazione matematica e costituisce pertanto un limite invalicabile nelle condizioni date, indipendentemente dalle tecnologie di trasmissione e dalle tecniche di correzione degli errori (nota 5).
Il teorema non fornisce alcuna indicazione numerica o tecnologica su come raggiungere tale velocità. Dà però alcuni suggerimenti utili su come aumentare la capacità di canale:
Utile vedere gli esempi 3 e 3bis ed i successivi esercizi.
Spesso il segnale analogico deve essere convertito in un segnale digitale attraverso un convertitore analogico digitale. Tale componente introduce un'approssimazione che può matematicamente essere espressa come rumore di conversione (o quantizzazione) in quanto appare sia nel dominio del tempo che in quello della frequenza come rumore bianco, cioè simile al rumore di origine termica.
Nel caso di un ADC ideale e di un segnale sinusoidale con ampiezza picco-picco pari al fondo scala dell'ADC, il rapporto segnale rumore è dato dalla formula:
SNR(dB) = 6.02·N + 1.76
Dove:
Simili considerazioni possono essere fatte relativamente al DAC (Digital to Analog Converter).
Utile vedere l'esempio 4 ed i successivi esercizi.
Negli ADC reali il SNR è inferiore a quanto dato dalla formula in quanto occorre tenere conto della presenza aggiuntiva del rumore interno di tipo analogico.
Spesso viene usato il termine ENOB (Effective Number Of Bits) per indicare il rumore effettivo; si parte dalla formula sopra riportata dove però SNR è noto perché misurato ed il numero di bit N è ricavato attraverso la formula inversa. Ovviamente N > ENOB; inoltre N è sempre un numero intero mentre ENOB è un numero reale.
L'ENOB dipende dalla qualità dell'ADC e dei circuiti che lo circondano, ma anche dalla sua tensione di alimentazione, dalla frequenza del segnale e dalla frequenza di campionamento.
Utile vedere l'esempio 5 ed i successivi esercizi.
Pagina creata nel marzo 2021
Ultima modifica: 13 novembre 2025
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)