Laboratorio: spettro di un segnale

Home → Tutorial → Appunti scolastici → Regime variabile → Laboratorio: spettro

In laboratorio è possibile fare misure sullo spettro di un segnale utilizzando:

un oscilloscopio digitale dotato di DFT (Discrete Fourier Transform) oppure più frequentemente FFT (Fast Fourier Transform)
un analizzatore di spettro come quello mostrato nella fotografia di apertura, strumento tipicamente usato per segnali a radiofrequenza

In questa pagina è descritto come utilizzare Picoscope 2205A MSO (software versione 7.1.2, l'ultima stabile nel momento della stesura di questa pagina), prodotto da Pico Technology. Prove analoghe sono mostrate con una versione precedente del software nella pagina Laboratorio: spettro di un segnale (v 6); con qualche variazione possono essere effettuate con qualunque oscilloscopio digitale moderno.

Attività 1

Generiamo un segnale sinusoidale con ampiezza di almeno 1 V e frequenza di qualche kHz (nell'esempio mostrato: V_P = 1,8 V e f = 7.5 kHz).

Prima di iniziare l'attività sperimentale:

disegnare a mano il segnale nel dominio del tempo
disegnare a mano lo spettro del segnale come valore efficace
disegnare a mano lo spettro di potenza in unità logaritmiche. Si consideri una resistenza di 10 kΩ.

Visualizziamo il segnale nel dominio del tempo collegando direttamente l'uscita del generatore di Funzioni all'ingresso dell'oscilloscopio:

Sonda collegata direttamente al GdF

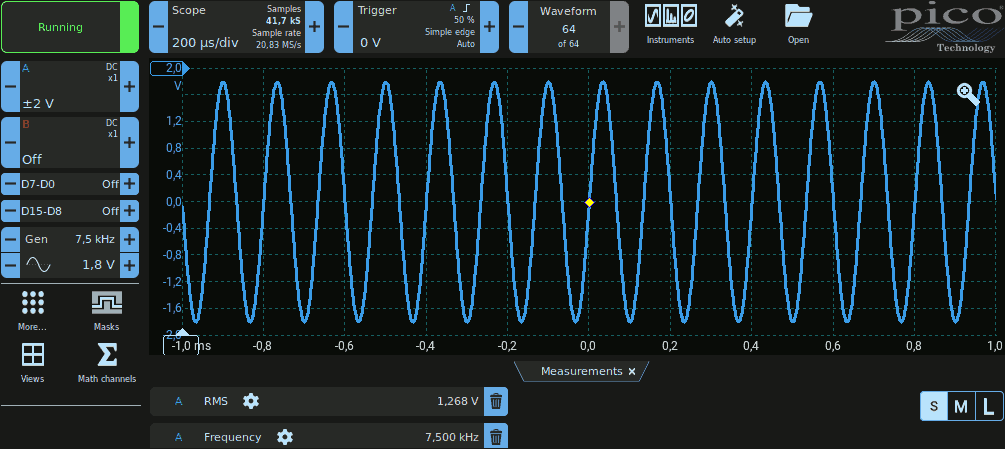
Sinusoide nel dominio del tempo

Per una migliore visualizzazione del segnale nel dominio della frequenza, è bene visualizzare nel dominio del tempo 10-20 periodi. Questa impostazione NON è quella consigliata per vedere correttamente il segnale nel dominio del tempo.

Per visualizzare lo spettro occorre utilizzare le icone Instruments e Spectrum, evidenziate nell'immagine seguente:

Lo spettro mostrato dall'oscilloscopio sarà piuttosto diverso da quanto atteso, a causa dell'uso di una scala logaritmica (nota 2) e di un intervallo molto ampio di frequenze (fino a 8 MHz).

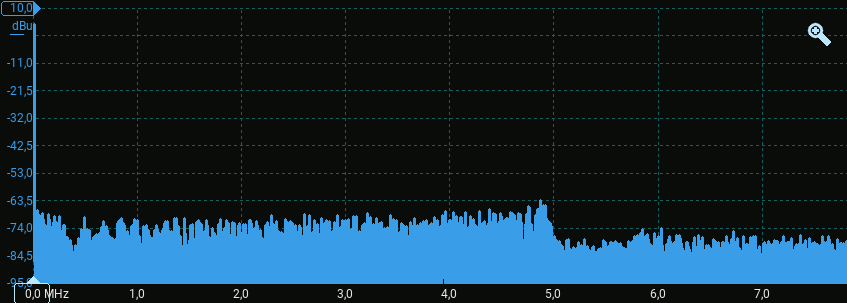
Spettro di una sunusoide (scala logaritmica)

Per questo è opportuno impostare nel menù Spectrum una frequenza massima pari a una decina di volte la frequenza della sinusoide (nota 3) ed una scala lineare per l'asse verticale.

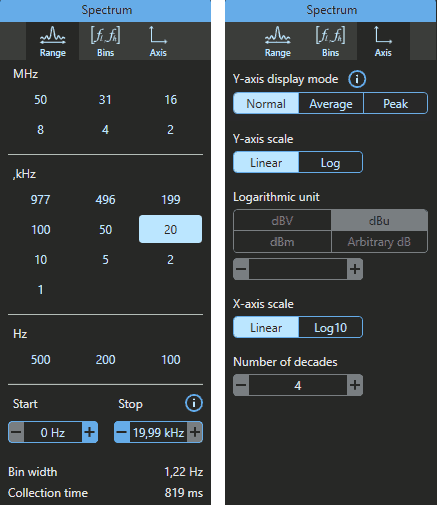
Impostazione della scala lineare

In alternativa, quando il grafico appare troppo "compresso", è possibile usare lo strumento Zoom, in alto a destra nell'immagine precedente.

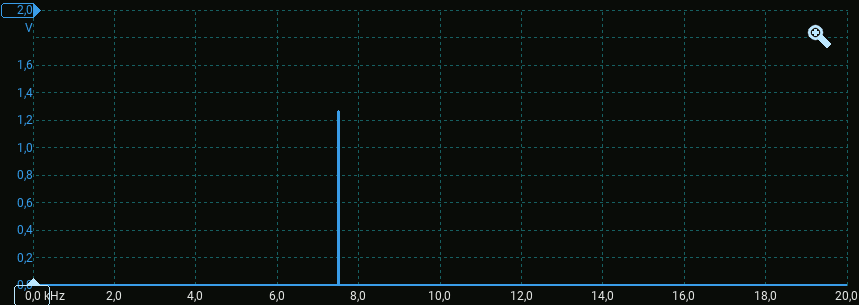
Attenzione: nel grafico è mostrata la tensione efficace (V_RMS), scelta preferita in ambito tecnico.

Attenzione: il valor medio mostrato non è corretto ed il manuale ne SCONSIGLIA la misura! (nota 5)

Prima di proseguire è utile osservare quanto mostrato nella casella Spectrum, di seguito evidenziata:

20 kHz è la massima frequenza presente sull'asse orizzontale del grafico
il Sample rate (frequenza di campionamento, misurata in kS/s) è pari al doppio della precedente frequenza. Questo valore è la condizione minima richiesta dal teorema del campionamento per campionare correttamente tutte le frequenza mostrate nel grafico; è di fondamentale importanza che il suo valore sia almeno il doppio di qualunque linea spettrale presente nel segnale reale!
Bins (la traduzione letterale come contenitore non aiuta a comprendere...) indica quante linee spettrali vengono calcolate dallo strumento. Per ragioni di efficienza computazionale (argomento complesso: Fast Fourier transform) sono sempre una potenza di due. Dividendo la frequenza per il numero di bins si ottiene la risoluzione spettrale (Bins width), ciò la distanza minima tra due linee spettrali affinché siano distinguibili.

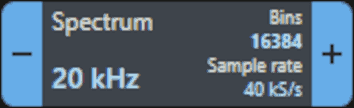
Per le misure è possibile utilizzare:

i Rulers (righelli). Per una misura accurata delle ampiezze delle linee spettrali è necessario impostare la funzione di window (nota 4) a Flat-top:

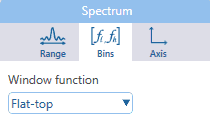
Window Flat-top

le misure automatiche (measurements). In questo caso è utile posizionare un ruler della frequenza sovrapposto ad una linea spettrale e specificare Peak nearest ruler 1 (oppure 2). Anche per le misure automatiche di ampiezza è necessario impostare la funzione di window (nota 4) a Flat-top:

Nell'immagine seguente sono mostrate entrambe le tecniche:

IMPORTANTE: l'aspetto più importante dell'attività è confrontare il grafico fatto manualmente con quello ottenuto con l'analizzatore si spettro, sia dal punto di vista grafico che numerico.

Lo spettro di potenza è visualizzato impostando gli assi in modalità logaritmica e scegliendo come unità di misura il dBm; inoltre è necessario specificare la resistenza che lo strumento userà nei calcoli.

Spettro in dBm

E' possibile effettuare le misure sia utilizzando i righelli che le misure automatiche. Anche in questo caso, per una misura accurata delle ampiezze delle linee spettrali, è necessario impostare la funzione di window (nota 4) a Flat-top:

IMPORTANTE: l'aspetto più importante dell'attività è confrontare il grafico fatto manualmente con quello ottenuto con l'analizzatore si spettro, sia dal punto di vista grafico che numerico.

Attività 1bis

Collegare al generatore di funzione un diodo ed una resistenza al 10 kΩ. Lasciare l'impostazione del generatore di funzioni come nella precedente attività.

Circuito non lineare

Visualizzare il segnale ai capi della resistenza nel dominio del tempo; dovrebbe essere simile al seguente:

Segnale unipolare

In base alle vostre conoscenze, disegnare a mano lo spettro del segnale, ovviamente passaggio fattibile solo parzialmente. In particolare: quale è la frequenza delle linee spettrali presenti?

Attenzione: il calcolo teorico dell'ampiezza delle linee spettrali non è presente in questo sito e, in ogni caso, è complesso e ricco di approssimazioni. Se chiedete ad una IA la risposta, per evitare risposte non corrette, occorre prestare molta attenzione nel porre la domanda (nota 6).

Visualizzare lo spettro in Picoscope, come descritto nella precedente attività. Attenzione: scegliere correttamente la frequenza di campionamento, in base alla risposta data qui.

Spettro del segnale raddrizzato

Misurare la tensione efficace delle linee spettrali e riportare i risultati in una tabella.

Avanzato: se avete chiesto ad una IA la soluzione numerica, verificate se è corretta o meno (nota 6).

Visualizzare lo spettro di potenza in unità logaritmiche.

Attività 2

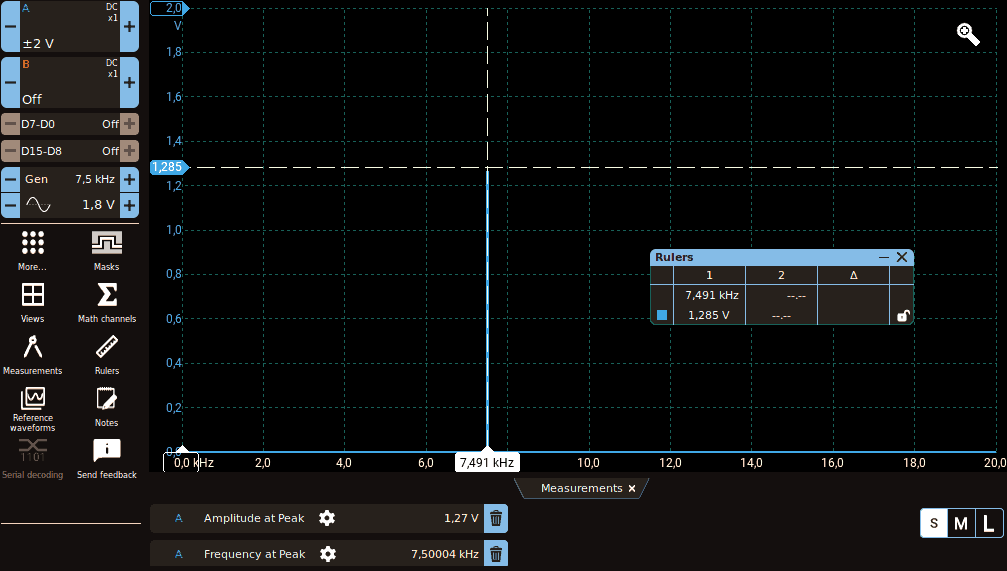
Generiamo un segnale ad onda quadra con ampiezza di 1 V e frequenza di esattamente 2 kHz (nota 1) e visualizziamolo nel dominio del tempo e della frequenza.

Prima di iniziare l'attività sperimentale:

disegnare a mano il segnale nel dominio del tempo
disegnare a mano lo spettro del segnale come valore efficace
disegnare a mano lo spettro di potenza in unità logaritmiche. Si consideri una resistenza di 10 kΩ.

Anche in questo caso lo spettro mostrato dall'oscilloscopio sarà piuttosto diverso da quanto atteso, ma procedendo come mostrato nell'Attività 1 si ottiene lo spettro seguente:

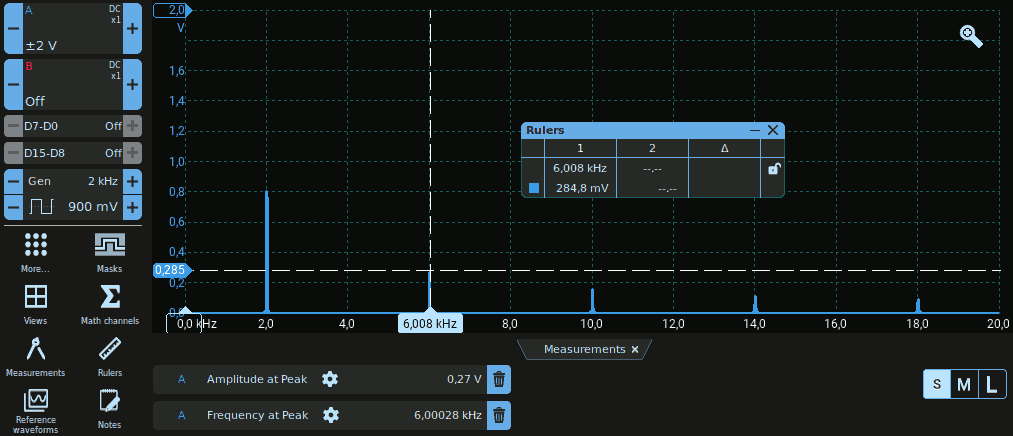
Spettro dell'onda quadra (2 kHz)

Con i ruler oppure gli strumenti automatici è possibile misurare l'ampiezza e la frequenza delle singole linee spettrali.

Attenzione: nel grafico è mostrata la tensione efficace (V_RMS), scelta preferita in ambito tecnico.

Attenzione: il valor medio eventualmente mostrato non è corretto! (nota 5).

Misurare la potenza delle singole linee spettrali in unità logaritmiche.

Confrontare i dati ottenuti con quanto previsto della teoria e, eventualmente, con quanto ottenuto con un simulatore, compilando la seguente tabella:

	Prima linea spettrale	Seconda linea spettrale	Terza linea spettrale	Quarta linea spettrale	...
Ampiezza di picco teorica
Ampiezza RMS teorica
Ampiezza RMS misurata
Ampiezza di picco simulata
Ampiezza RMS simulata
Frequenza teorica
Frequenza misurata
Frequenza simulata
Potenza teorica (mW)
Potenza teorica (dBm)
Potenza misurata (dBm)

IMPORTANTE: l'aspetto più importante dell'attività è confrontare il grafico fatto manualmente con quello ottenuto con l'analizzatore di spettro (ed eventualmente con il simulatore), sia dal punto di vista grafico che numerico.

Attività 3

L'immagine seguente contiene una significativa incongruenza, almeno apparentemente: il generatore di funzioni genera una sinusoide con frequenza 12 kHz, ma lo spettro mostra una sinusoide con frequenza 8 kHz. Perché?

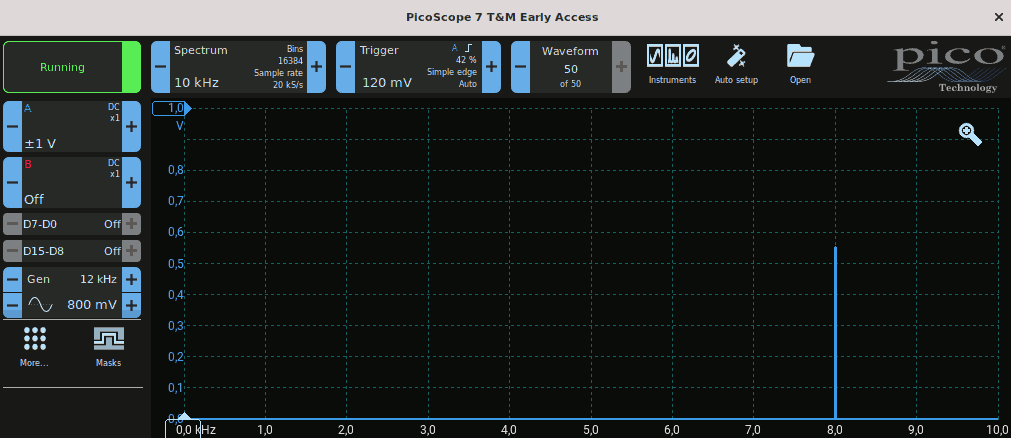
Per rispondere alla domanda:

quale è la frequenza della sinusoide generata dal generatore di funzioni?
quale è la frequenza di campionamento utilizzata?
quale è la frequenza di campionamento richiesta dal teorema del campionamento?

Attività 4

Generiamo un segnale ad onda quadra con ampiezza di circa 1 V e frequenza di 3 kHz. In base alla teorema delle serie di Fourier, questo segnale contiene infinite linee spettrali con frequenza multiplo intero dispari di 3 kHz.

Procedendo allo stesso modo mostrato nelle precedenti attività però lo spettro visualizzato contiene una serie di linee che non dovrebbero essere presenti, indicate dalle frecce rosse nell'immagine che segue:

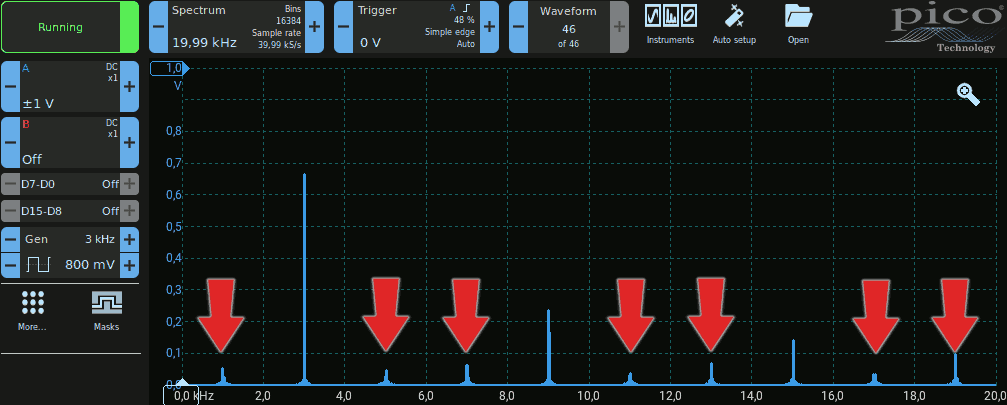
Il motivo deriva dal mancato rispetto del teorema del campionamento:

l'onda quadra contiene un numero molto elevato di linee spettrali, teoricamente infinito : 3 kHz, 9 kHz, 15 kHz, 21 kHz, 24 kHz...
la frequenza di campionamento scelta è pari a 40 kHz, come mostrato dall'oscilloscopio
le linee spettrali con frequenza oltre i 20 kHz causano aliasing, cioè segnali che nella realtà non esistono...

Per risolvere il problema è necessario aumentare in modo significativo la frequenza di campionamento, fino a quando le linee spettrali diventano sufficientemente piccole per poter essere ignorate. Di seguito un esempio, migliorabile dal punto di vista della visualizzazione con lo Zoom (non mostrato):

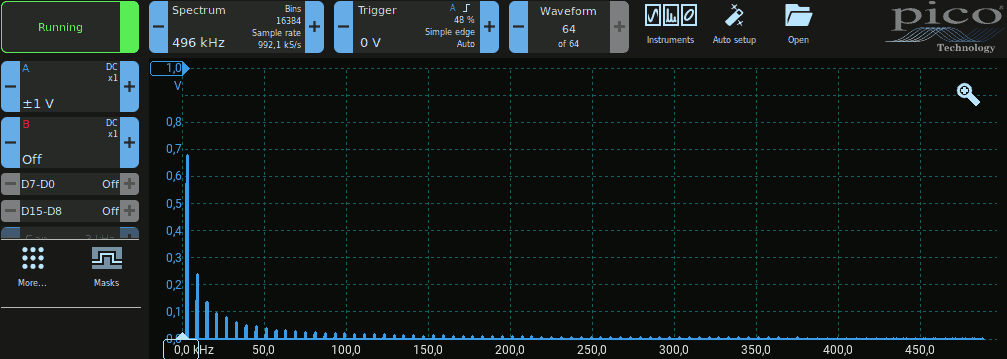
Spettro esteso

cosa succede se si aumenta o diminuisce (di poco) la frequenza del segnale?
cosa succede se si aumenta o diminuisce (di poco) l'ampiezza del segnale?

Attività 5

Generare un segnale rettangolare con frequenza di 5 kHz, ampiezza ±400 mV e Duty Cycle del 20%, utilizzando il generatore arbitrario di segnali (AWG). Visualizziamo il segnale nel dominio del tempo (consiglio: verificare con attenzione che le impostazioni siano corrette!) ed in quello della frequenza.

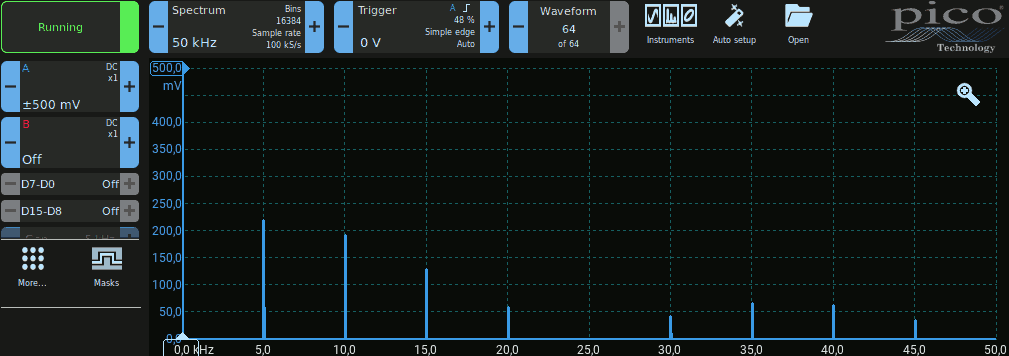
Spettro di un segnale rettangolare

Confrontare lo spettro con quanto previsto dalla teoria e con i risultati della simulazione.

Completare la seguente tabella (le prime due righe sono un'attività avanzata, da compilare utilizzando la formula contenuta nel Formulario):

	Prima linea	Seconda linea	Terza linea	Quarta linea	Quinta linea	Sesta linea	...
Ampiezza di picco teorica	30 mV	24 mV
Ampiezza RMS teorica	21 mV	17 mV
Ampiezza RMS misurata
Ampiezza di picco simulata
Ampiezza RMS simulata
Frequenza teorica
Frequenza misurata

[Approfondimento] Attività 6

Esplorare lo spettro di altri segnali (triangolare, a denti di sega...) individuando gli aspetti descritti nella pagina Serie di Fourier.

[Approfondimento] Attività 7

Un segnale sweep (da "spazzare") è un segnale sinusoidale la cui frequenza passa con continuità da un valore ad un altro.

Per generarlo con il generatore di funzioni interno a Picoscope occorre impostare la corrispondente voce del menu. Per esempio le seguenti impostazioni generano una sinusoide la cui frequenza varia da 8 kHz a 10 kHz e viceversa (Up Down) cambiando di 100 Hz ogni 200 µs.

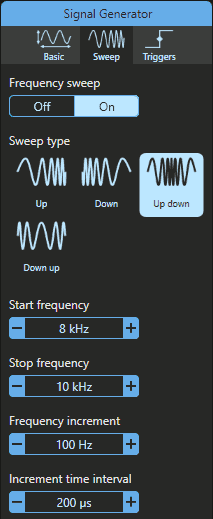
Lo spettro, piuttosto sorprendente, è mostrato nell'immagine seguente:

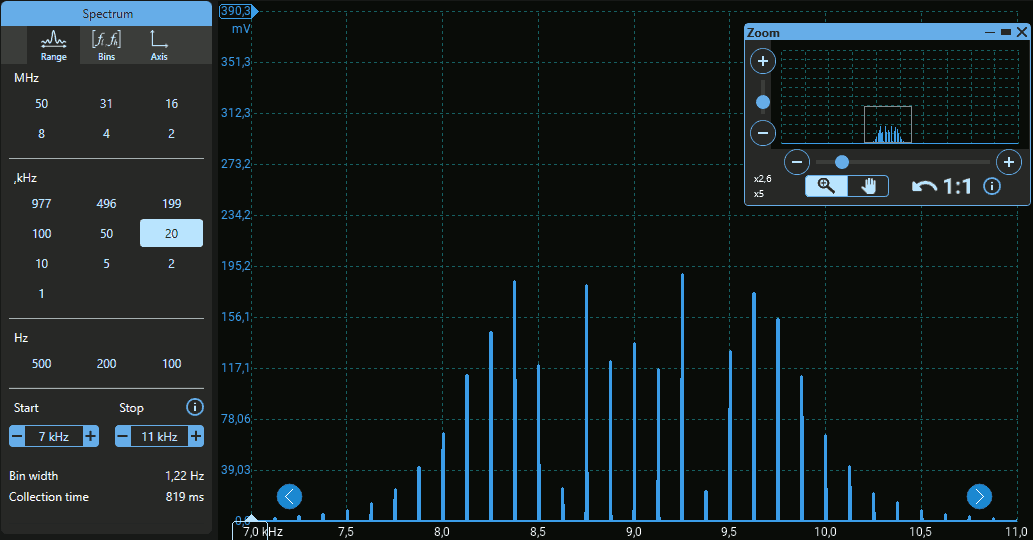
Spettro del segnale FM

Descrizione:

sono presenti numerose linee spettrali la cui ampiezza varia in modo apparentemente casuale
le linee più ampie sono comprese tra circa 7,5 kHz e 10,5 kHz (ma sono presenti anche altre piccole linee spettrali)
le linee sono praticamente disposte simmetricamente rispetto alla frequenza di 9 kHz

Queste caratteristiche sono simili allo spettro della modulazione di frequenza usata nelle trasmissioni radio FM da oltre 50 anni.

[Approfondimento] Attività 8

Generare un segnale digitale semi-casuale (PRBS, Pseudo Random Binary Sequence) se disponibile. In alternativa, utilizzare Arduino per generare una sequenza seriale continuamente variabile, da trasmettere con l'interfaccia SPI (attività 1).

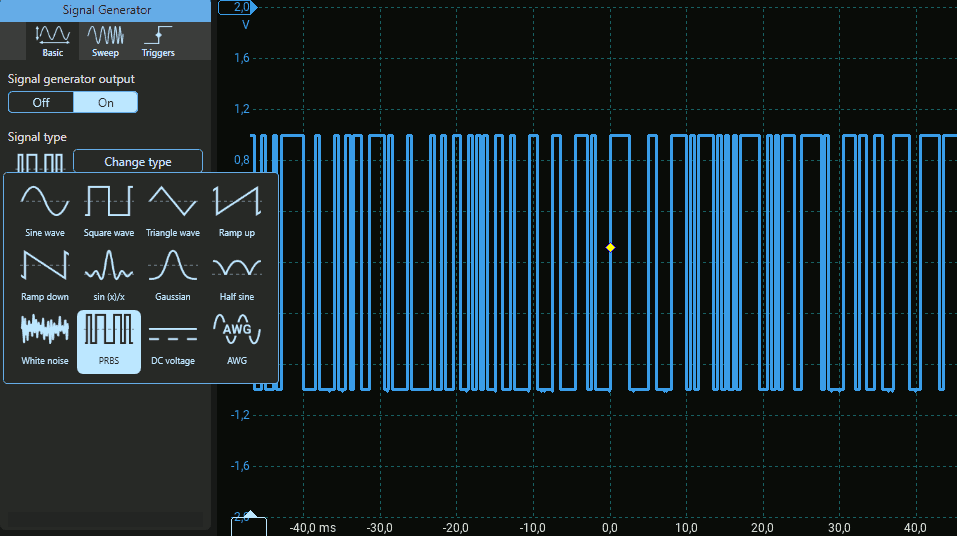
Analizzare lo spettro del segnale e confrontarlo con quanto descritto alla pagina Trasformata di Fourier.

Attività 9

In molte situazioni l'ampiezza delle linee spettrali è misurata in dBV (per le tensioni) oppure dBm (per le potenze).

La misura in dBV viene effettuata impostando l'asse Y in modalità logaritmica e scegliendo come unità di misura il dBV:

Misura in dBV

Il grafico mostrato è simile al seguente, relativo ad un segnale sinusoidale.

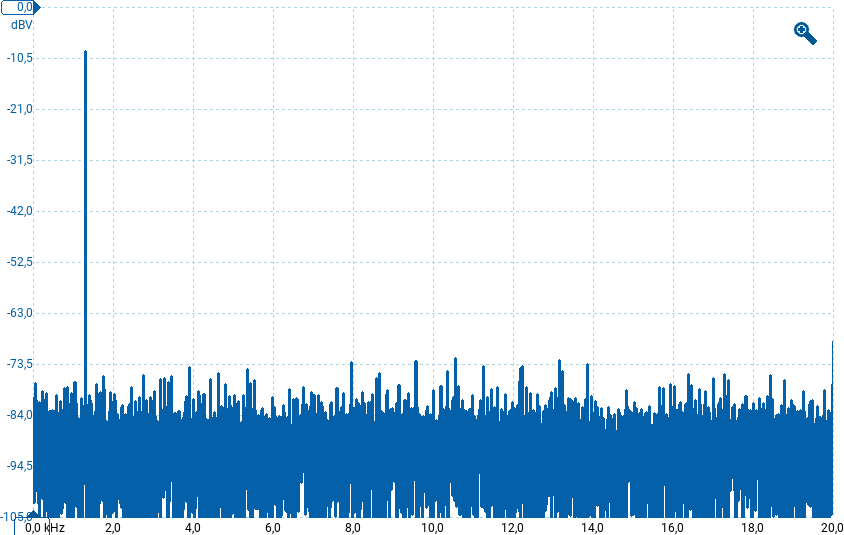
Spettro di una sinusoide con unità logaritmiche

Oltre alla linea in corrispondenza della frequenza della sinusoide, si notano numerosissime linee con ampiezza casuale e MOLTO più piccole della sinusoide. Si tratta del rumore di quantizzazione: esso ha, nell'esempio mostrato, ampiezza di circa -75 dBV ed è circa 65 dB inferiore all'ampiezza della sinusoide.

L'ampiezza della sinusoide può essere misurata con i rulers. Per una misura accurata è necessario impostare anche in questo caso la funzione di window a Flat-top.

Generare un segnale sinusoidale con ampiezza di circa 1 V e frequenza di circa 2 kHz
Visualizzare lo spettro con ampiezza espressa in dBV
Confrontare il valore misurato con i cursori con quanto calcolabile con le formule teoriche. Nell'analisi dei dati prestare particolare attenzione al legame tra tensione di picco ed efficace, quando espresse in unità lineari o logaritmiche!

Ampiezza teorica di picco - V
Ampiezza teorica RMS - V
Ampiezza teorica di picco - dBV
Ampiezza teorica RMS - dBV
Ampiezza misurata RMS - dBV

Attività 10

Lo spettro di potenza è visualizzato impostando gli assi in modalità logaritmica e scegliendo come unità di misura il dBm; inoltre è necessario specificare la resistenza che sceglieremo.

Spettro in dBm

Il grafico mostrato è simile al seguente, non molto diverso dal precedente se non per il fatto che si tratta di uno spettro di potenza:

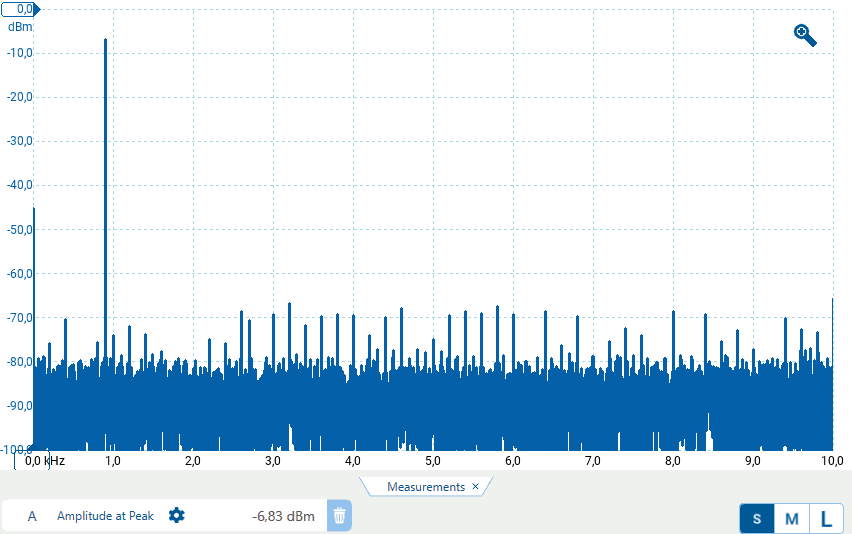
L'ampiezza della sinusoide può essere misurata con i rulers. Per una misura accurata è necessario impostare anche in questo caso la funzione di window a Flat-top.

Generare un segnale sinusoidale con ampiezza di circa 1 V e frequenza di circa 2 kHz
Visualizzare lo spettro di potenza
Confrontare il valore misurato con i cursori con quanto calcolabile con le formule teoriche. Nell'analisi dei dati prestare particolare attenzione al legame tra tensione di picco ed efficace, quando espresse in unità lineari o logaritmiche! Ed anche tra valore efficace e potenza.

Ampiezza teorica RMS - V
Potenza teorica - mW
Potenza teorica - dBm
Potenza misurata - dBm

Attività 11

Generare un segnale ad onda quadra di circa 500 mV e visualizzare lo spettro in dBV e quello in dBm. Molto probabilmente, oltre al rumore, sarà presente anche l'effetto dell'aliasing (perché?)

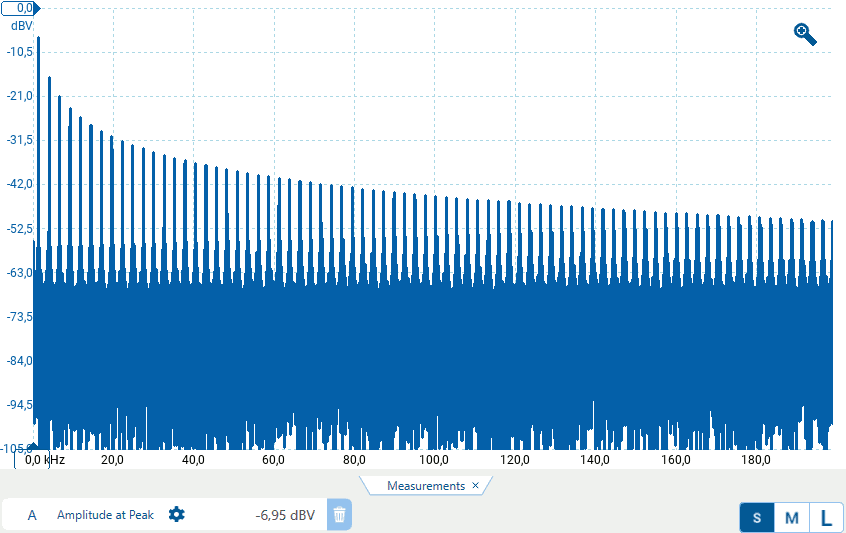
Spettro dell'onda quadra - dBV

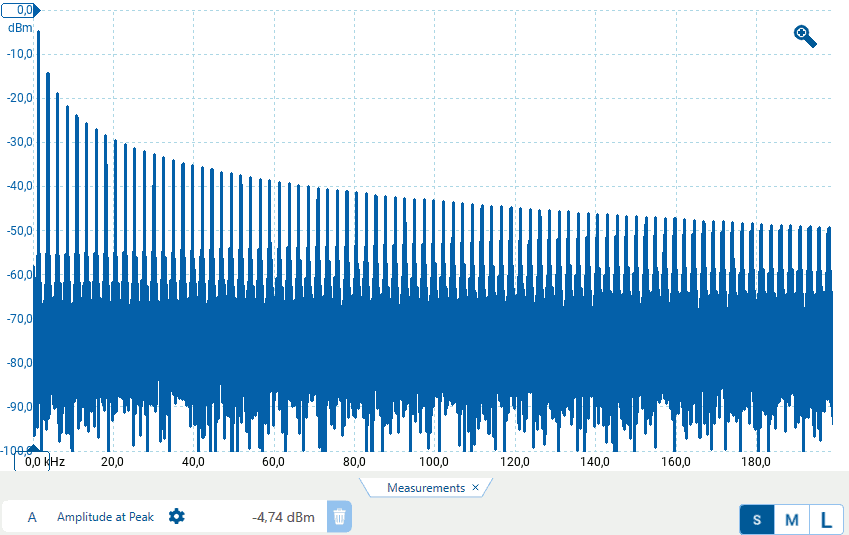
Confrontare i valori misurati per le ampiezza delle prime linee spettrali con quelli teorici (la prima colonna della tabella è esemplificativa, da modificare con i propri dati)

	Prima linea spettrale	Seconda linea spettrale	Terza linea spettrale	Quarta linea spettrale	...
Ampiezza teorica di picco - V	0.637 V
Ampiezza teorica RMS - V	0.450 V
Ampiezza teorica di picco - dBV	-3,92 dBV
Ampiezza teorica RMS - dBV	-6.93 dBV
Ampiezza misurata RMS - V	0.45 V
Ampiezza misurata RMS - dBV	-6.95 dBV
Potenza teorica - mW	0.338 mW
Potenza teorica - dBm	-4.71 dBm
Potenza misurata - dBm	-4.74 dBm

Attività 12

In alcune situazioni può essere utile visualizzare l'asse delle frequenza su scala logaritmica e l'asse verticale come dBV o dBm, ottenendo quello spesso indicato come grafico semi-logaritmico:

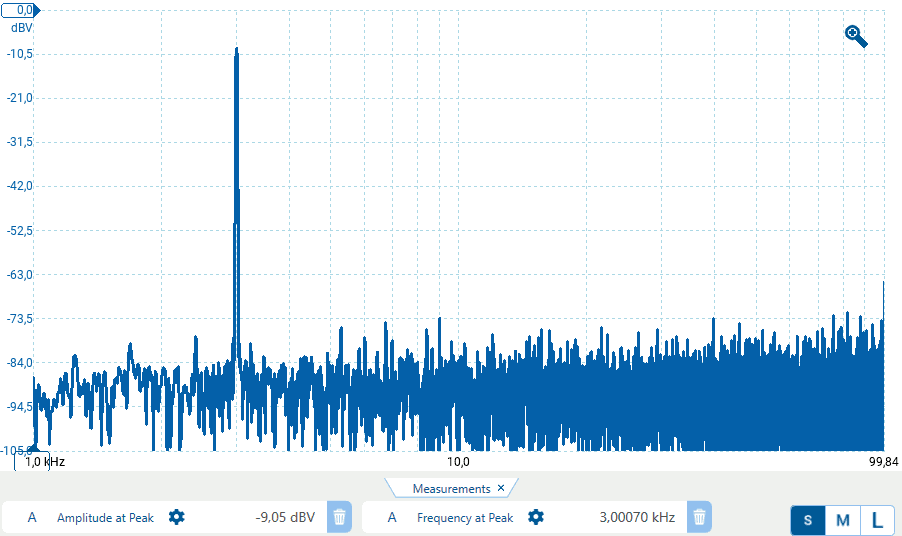
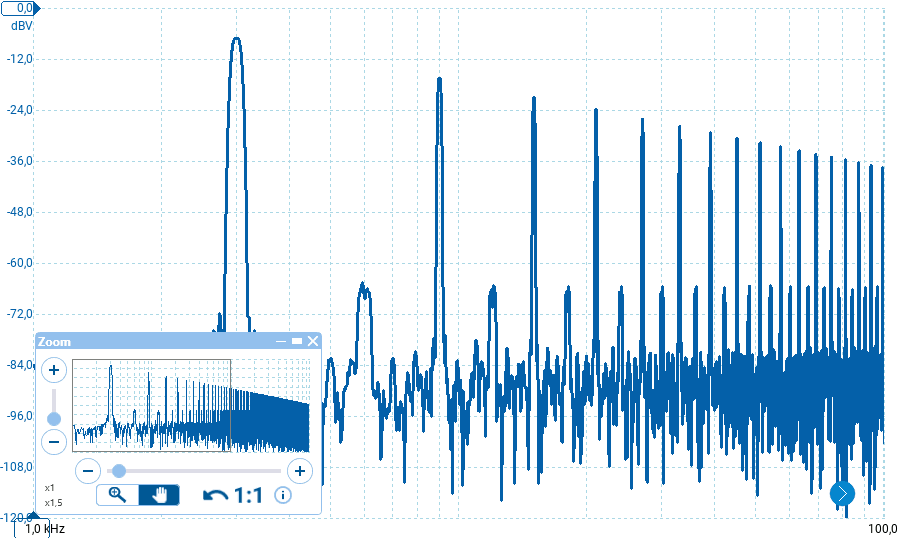
Di seguito come appare lo spettro di una sinusoide e di un'onda quadra su grafico semilogaritmico:

Note

Si tratta di una caso particolare che, in funzione della frequenza di campionamento, non crea evidenti problemi di aliasing, come descritto nell'attività 3
Nelle misure reali viene in genere preferita la scala logaritmica per le tensioni, ma questa tende a confondere se non è ben chiaro il suo significato
Nel caso di segnali sinusoidali non sono necessari particolari accorgimenti nella scelta della frequenza di campionamento, purché sia rispettato il teorema del campionamento
Le funzioni di window sono un argomento piuttosto avanzato dell'analisi spettrale. La necessità del loro uso deriva dalla non sincronicità della frequenza di campionamento con quella del segnale e permettono di avere una migliore stima dell'ampiezza oppure della frequenza del segnale (non di entrambe contemporaneamente)
Avanzato - Questo strano comportamento deriva dal fatto che l'algoritmo calcola lo spettro bilatero e mostra quello unilatero. Inoltre la misura del valor medio mostrata dipende dai parametri con cui è configurata la FFT. Banalmente è il tentativo di una giustificazione tecnica di un bug...
Per esempio Gemini Pro e chatGPT tendono a dare risposte basate su approssimazioni non corrette (coseno rialzato piuttosto che raddrizzatore ideale...), applicando formule teoriche al di fuori del loro campo di validità

Data di creazione di questa pagina: ottobre 2020
Ultima modifica: 17 settembre 2026