Trasformata Discreta di Fourier

Tutorial → Appunti scolastici → Appunti sparsi → DFT

In questa pagina esamineremo come ricavare lo spettro di un segnale periodico digitalizzato. Facciamo le seguenti ipotesi

il segnale analogico è stato campionato rispettando il teorema di Whittaker-Nyquist-Kotelnikov-Shannon (o del campionamento). Questa ipotesi è non derogabile
il segnale analogico è periodico. In realtà questa ipotesi è sempre vera se consideriamo il segnale solo dopo un campionamento eseguito con un numero finito N di campioni.
il segnale analogico è stato campionato in modo sincrono, cioè il periodo del segnale analogico contiene esattamente un numero intero N di campioni. Questa ipotesi, decisamente difficile da ottenere nel mondo reale, verrà rimossa più avanti.

In queste condizioni periodo del segnale ed intervallo di campionamento coincidono, eventualmente a meno di multipli.

Analisi intuitiva

Il segnale campionato è composto da N valori ed è memorizzato in un vettore che indicheremo con x (minuscolo), essendo x(n) il valore del campione ennesimo. Tali campioni si estendono esattamente su un periodo del segnale (o al limite su un numero intero di periodi del segnale).

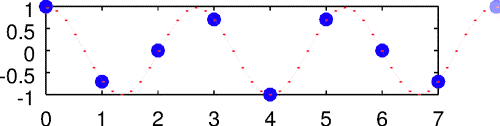
Per esempio consideriamo il seguente segnale, composto da 8 campioni (e arbitrariamente reso periodico, con periodo pari a 8 bin)

Tale segnale, in base al teorema delle serie di Fourier, è scomponibile nella somma di:

Un valor medio
Una sinusoide con periodo pari al periodo del segnale; ampiezza e fase sono da calcolare
Una sinusoide con periodo pari a metà del periodo del segnale (cioè con frequenza doppia di quella del segnale); ampiezza e fase sono da calcolare
Una sinusoide con periodo pari ad un terzo del periodo del segnale (cioè con frequenza tripla di quella del segnale); ampiezza e fase sono da calcolare
...

La sinusoide con frequenza più alta è, in base al teorema del campionamento, quella con frequenza pari alla metà della frequenza di campionamento, cioè con periodo pari a 2 campioni. Complessivamente avremo calcolato N/2 valori per l'ampiezza (considerando anche il valor medio) ed altrettanti per la fase.

In realtà si preferisce pensare a ciascuna sinusoide con fase come somma di una sinusoide e di una cosinusoide, ciascuna con opportuna ampiezza ( e fase nulla). Questo perché gli integrali definiti qui descritti danno un metodo di calcolo:

Si prendono le cosinusoidi con frequenza pari a quella del segnale, cioè periodo pari a N, N/2, N/3, N/4... [bin]. Queste cosinusoidi campionate sono visualizzate nei grafici seguenti, nella colonna di sinistra (nota 1)
Si moltiplica ciascuna cosinusoide per il segnale misurato e se ne calcola l'integrale definito. Il significato del risultato già lo conosciamo: un numero proporzionale all'ampiezza dell'armonica con l stessa frequenza della cosinusoide considerata
Si ripete la stessa operazione con le sinusoidi (grafici di destra)
Infine si calcola la media dei campioni, il valor medio

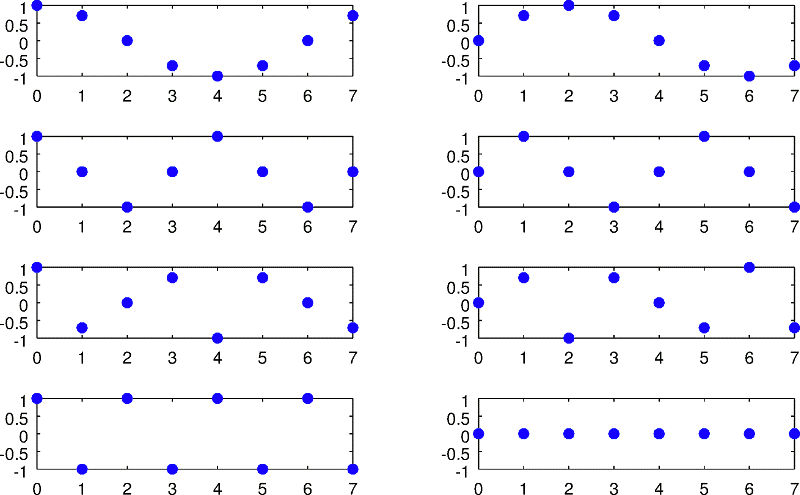
In genere i numeri ottenuti dalla prima colonna sono memorizzati in un vettore Xr(n), vettore con la parte reale. I numeri ottenuti dai grafici di destra sono memorizzati in Xi(n), vettore con la parte immaginaria.

Le formule

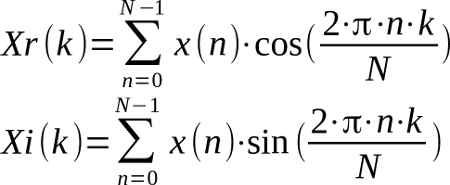
DFT: le formule

Note

Le sinusoidi disegnate nella prima, nella seconda e nella quarta riga sono facilmente visibili. Se non avete fantasia potreste avere difficoltà nell'individuare la sinusoide nei grafici della terza riga. Forse la figura seguente può aiutare:

Data di creazione di questa pagina: 1 aprile 2017
Ultima modifica: