
In questa pagina e nelle seguenti verranno presentati alcuni concetti utili per comprendere le tecniche di analisi digitale dei segnali, con particolare riferimento all'analisi spettrale. Il target sono studenti della classe quinta dell'Istituto tecnico ad indirizzo informatico/telecomunicazioni/elettronico; alcuni concetti matematici verranno ridotti al minimo indispensabile, favorendo per quanto mi è possibile una visione grafica ed intuitiva.
Prima di iniziare, è doveroso riprendere alcuni concetti che dovrebbero essere ben noti. Giusto per confondere un po' le acque.
![]() Da fare
Da fare
Ho cominciato scrivendo poca matematica... e già non mantengo la parola!
Chiunque abbia affrontato la trigonometria si sarà imbattuto in una serie di formule da imparare a memoria. Ne servirà una sola (e altre simile, che qui neppure riporto):
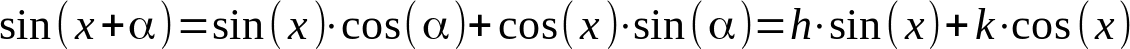
I termini usati:
Leggiamone il significato in termini di segnali: una qualunque sinusoide con fase è scomponibile nella somma di una sinusoide e di una cosinusoide di opportuna ampiezza.
Proseguendo il ragionamento: una qualunque sinusoide con fase è descrivibile con un numero complesso, usando il cosiddetto metodo simbolico
Penso che quanto di seguito riportato siano esercizi classici della prima verifica di matematica sugli integrali definiti. A voi l'onore e l'onere della risoluzione analitica, cosa per me oltremodo ostica.
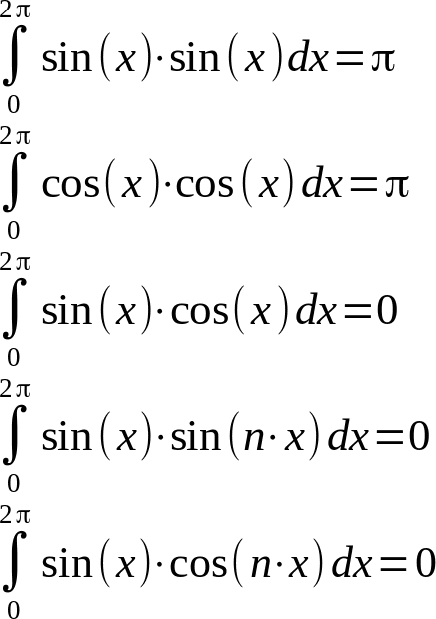
In pratica: l'integrale definito su un periodo del prodotto di due funzioni seno e coseno con periodo multiplo uno dell'altro danno sempre come risultato zero, tranne i primi due casi mostrati in cui le due funzioni sono identiche, in pratica sin2(x) e cos2(x).
Seno e coseno sono un esempio di funzioni ortogonali tra di loro. Disegnando il grafico della funzioni la cosa è anche assolutamente intuitiva in quanto le aree positivi e quelle negative si equivalgono.
Infine, il seguente integrale è pari ad un numero compreso tra 0 e π, a seconda del valore di α, cioè della fase
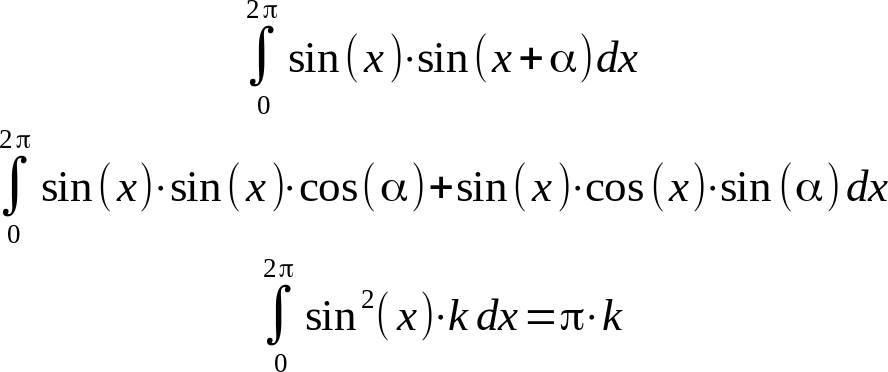
Gli stessi passaggi valgono anche nel caso delle cosinusoidi.
In pratica, conclusione del paragrafo matematico:
Il concetto di segnale periodico dovrebbe essere assolutamente chiaro... O no?
In matematica, a livello intuitivo, per funzione periodica si intende una funzione che assume valori che si ripetono esattamente ad intervalli regolari; questo intervallo viene chiamato periodo. Per esempio la funzione y = cos (x) è considerata periodica, cosa intuitivamente descritta dal suo grafico, evidentemente da prolungare a destra e sinistra all'infinito (nota 1):

Al contrario una funzione non periodica è (sorprendentemente!) definita come una funzione che non è periodica.
Domanda: esistono segnali periodici? Esistono segnali non periodici?
La risposta ad entrambe le domanda è sia positiva che negativa, a seconda degli aspetti che vogliamo mettere in evidenza nel nostro modello di realtà. Per esempio:
Possiamo dire che nel mondo reale il concetto di periodicità è strettamente legato al tempo di osservazione. Questo evidentemente non ha impedito di dotarci di strumenti matematici diversi per studiare l'uno e l'altro. Per esempio le Serie di Fourier per i segnali periodici e le Trasformate di Fourier per i segnali non periodici, con spettri rispettivamente discreti e continui.
Se il segnale viene campionato, la definizione di periodicità è ulteriormente complicato dalla presenza di un secondo periodo, quello di campionamento.
Per esempio nella figura seguente un segnale viene campionato 32 volte, indicato dai punti (bin) in blu; è assolutamente intuitivo pensare di prolungare a destra e a sinistra, all'infinito, tali punti ed ottenere così un segnale periodico. Ovviamente questa operazione intuitiva è anche assolutamente arbitraria, in quanto partendo da pochi dati reali ci siamo arrogati il diritto di ottenere infiniti dati.

Questa operazione è possibile solo perché nell'intervallo in cui sono stati prelevati i campioni (pari ai 32 bin blu) è presente esattamente un numero intero di periodi (due nell'esempio). Detto in altro modo, l'operazione è possibile solo perché il periodo del segnale è un multiplo intero del periodo di campionamento. O anche: la frequenza di campionamento è un multiplo intero della frequenza del segnale. Esattamente un multiplo intero! Possiamo anche dire che il periodo del segnale coincide, a meno di un fattore moltiplicativo intero, con l'intervallo di campionamento. Per i nostri fini è assolutamente equivalente dire che il periodo del segnale è 16 oppure 32 bin
Tale tipo di campionamento è detto sincrono.
Inizialmente considereremo il solo campionamento sincrono, con buona pace del nostro intuito ed anche dei matematici, che avranno finalmente a che fare con un segnale (artificiale) davvero periodico.
Se non viene rispettato il vincolo che lega i due periodi di campionamento e del segnale, diventa problematica la ricostruzione intuitiva del segnale (sempre arbitraria, comunque). Per esempio la figura seguente mostra come, sempre partendo dai 32 punti blu affiancato dalla sua estensione a destra e a sinistra, il segnale ricostruito sia ben diverso da quanto l'intuito ci suggerisce; ciò rende per esempio problematico addirittura definire il concetto apparentemente banale di periodo del segnale.

Ma possiamo anche andare oltre: data una qualunque sequenza di campioni, possiamo (arbitrariamente) ripetere tale sequenza un numero infinito di volte rendendo un segnale qualunque periodico, come nei due casi precedenti. Che poi ciò coincida o meno con la realtà poco ci importa, perché gli unici segnali reali sono quelli campionati.
Questo di fatto rende nulla la differenza tra un segnale campionato periodico ed uno non periodico.
Come dimostrò 200 passa anni fa Jean Baptiste Joseph Fourier, un segnale periodico può essere scomposto in una somma di sinusoidi e cosinusoidi con frequenza multipla intera della frequenza del segnale più una valore costante. La cosa è tutt'altro che intuitiva, al punto che matematici del calibro di Joseph-Louis Lagrange non ne furono convinti per almeno un decennio, fino alla loro morte. (nota 2)
![]() Da fare
Da fare
Data di creazione di questa pagina: 1 aprile 2017
Ultima modifica:
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)