Prima di procedere è bene aver chiaro i concetti di tensione efficace, potenza media ed attenuazione, sia usando unità di misura lineari che logaritmiche, rumore termico, SNR e capacità di canale.
Un segnale sinusoidale con frequenza 10 MHz e potenza 0 dBm è applicato ad un doppino AWG22 lungo 300 ft (circa 90 m), correttamente terminato (Z0 = 100 Ω). Calcolare:
Il produttore fornisce il seguente grafico (con misure imperiali...):
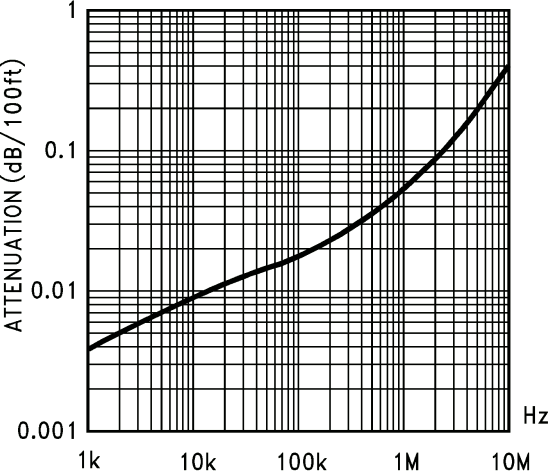
Dal grafico leggiamo che l'attenuazione di 100 ft di cavo alla frequenza di 10 MHz è circa 0,4 dB. Quindi 300 ft hanno un'attenuazione di 1,2 dB,
La potenza d'uscita è:
Pout = Pin - α = 0 dBm - 1,2 dB = -1.2 dBm
Ovviamente la potenza d'uscita è minore di quella di ingresso. Perché?
Se richiesto (ma in genere non lo è...) possiamo anche calcolare che la potenza di ingresso è 1 mW e la potenza di uscita 0,75 mW: basta applicare le equivalenze tra misure logaritmiche e lineari.
Il testo del problema non fornisce la velocità di propagazione del segnale. Esso può essere:
Scegliamo la terza opzione, in mancanza di meglio. Il tempo di propagazione tP è:
tP = 90 / 200·106 = 450 ns
L'impedenza caratteristica del cavo è un dato (Z0 = 100 Ω). Quindi per un uso corretto deve essere:
La tensione sinusoidale di ingresso ad una linea AWG22 terminata lunga 1 km ha ampiezza efficace 5 V e frequenza 1 MHz. Determinare l'ampiezza del segnale di uscita ed il tempo di propagazione (nota 1).
Il cavo ha lunghezza 3280 ft (!).
L'attenuazione per un cavo lungo 100 ft è circa 0,05 dB, come si può leggere nel grafico relativo ad AWG22; quindi l'attenuazione è:
α = 0,05 · 3280 / 100 = 1,6 dB
La tensione di ingresso è circa 14 dBV.
La tensione di uscita è quindi circa 12,4 dBV (circa 4,2 V).
Il tempo di propagazione:
t = 1 000 / 2·108 = 5 µs
Una linea ha attenuazione di 10 dB e impedenza caratteristica 50 Ω; è correttamente terminata. L'ingresso è una tensione sinusoidale con ampiezza massima 12 V. Determinare la potenza del segnale di uscita (nota 1).
VINRMS = 12 / √2 = 8.5 V
PIN = 8.52 / 50 = 1,44 W = 31.6 dBm
POUT = 31.6 - 10 = 21.6 dBm (= 10(21.6/10) = 144 mW = 0,144 W))
VINRMS = 8.5 V = 18.6 dBV
VOUTRMS = 8.6 dBV = 2,7 V
POUT = 0,144 W (= 21.6 dBm = -8.4 dBW)
VINP = 21.6 dBV
VOUTP = 11.6 dBV = 3,8 V
VOUTRMS = 2,7 V
POUT = 0,144 W (= 21.6 dBm)
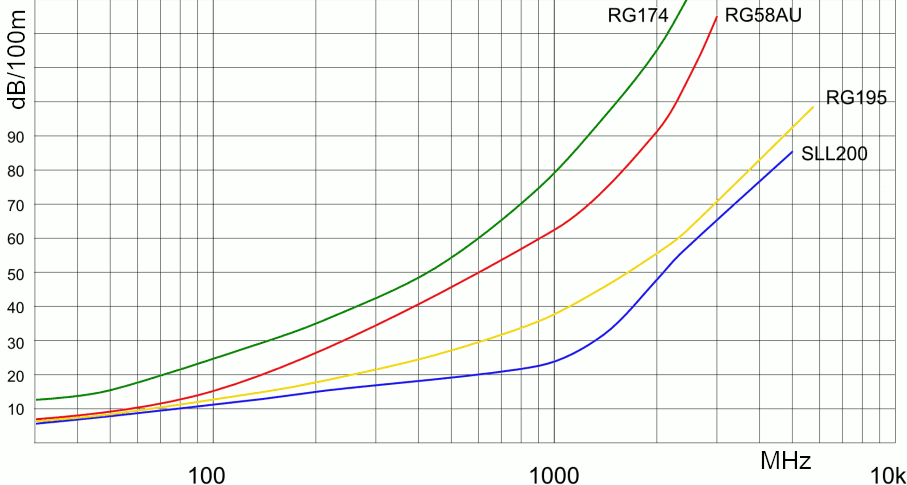
Un cavo di tpo RG174 è utilizzato per trasmettere segnali con frequenza di 100 MHz e banda 50 MHz. Il trasmettitore ha una potenza di 20 dBm. Il grafico di apertura mostra quanto vale l'attenuazione di 100 m di cavo, al variare della frequenza.
Calcolare:
Dal grafico (curva verde) possiamo vedere che, alla frequenza di 100 MHz, l'attenuazione di 100 m di cavo è circa α100m = 25 dB/100 m. L'attenuazione totale è quindi α = 100 dB.
In questo calcolo è stata introdotta un'approssimazione in quanto l'attenuazione andrebbe calcolata per tutte le frequenze comprese tra 75 MHz e 125 MHz cioè per tutte le frequenza comprese nell'intervallo di 50 MHz nell'intorno di 100 MHz.
La potenza del segnale ricevuto in uscita al cavo va calcolato con la formula del bilancio di potenza. Non essendo presenti amplificatori questa divente semplicemente la differenza tra potenza di ingresso e attenuazione:
SOUT = SIN - α = -80 dBm
Il rumore termico dipende da temperatura (in assenza di dati ipotizzata a 17 °C) e banda:
N = 10 · log(1,38 · 290) + 10 · log( 50·106 ) - 200 = -97 dBm
Il rapporto segnale rumore all'uscita della linea di trasmissione:
SNR = -80 + 97 = 17 dB
C = 17 · 50·106 / 3 = 280 Mbit/s
Possiamo ipotizzare una velocità di v = 200·106 m/s (nota 2)
TP = 400 / 200·106 = 2 µs
Trovare la capacità di canale ed il tempo di percorrenza per i cavi SLL200, RG195 e RG58AU. Tutti i dati sono quelli del precedente esempio.
Risultati:
| α [dB] | SOUT [dBm] | SNR [dB] | C [Mbit/s] | Tp [ns] | |
| SLL200 | 48 | -28 | 69 | 1143 | 1600 |
| RG195 | 52 | -32 | 65 | 1077 | 1900 |
| RG58AU | 60 | -40 | 57 | 944 | 2000 |
Un segnale con potenza 0 dBW e frequenza 1 GHz è trasmesso a 200 m con un cavo RG195. Quale è la potenza del segnale ricevuto? Cosa cambia se si utilizza un cavo SLL200?
Se la potenza viene portata a 2 W, quale potenza viene ricevuta nelle stesse condizioni?
Il cavo richiede, per essere collegato alle apparecchiature, un connettore (anzi: due) la cui perdita di inserzione vale tra 2 dB. Come cambia la potenza del segnale ricevuto considerando anche questa attenuazione?
Un'antenna WiFi dual band è posta sul tetto di un edificio ed è collegata al trasmettitore, posto all'interno, con 10 m di cavo coassiale.
Quale tipo di cavo conviene utilizzare tra quelli presenti in questo grafico?
Facendo le opportune ipotesi, quanto vale l'attenuazione dovuta al cavo e ai connettori?
La massima EIRP legalmente ammessa in Europa per un segnale a WiFi 2.4 GHz è 20 dBm. Quale può essere la massima potenza in uscita al trasmettitore?
La massima EIRP legalmente ammessa in Europa per un segnale WiFi a 5.2 GHz è 30 dBm. Quale può essere la massima potenza in uscita al trasmettitore?
Pagina creata nel marzo 2021
Ultima modifica: 5 febbraio 2026
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)
