
In questa pagina vedremo come utilizzare MPLAB MINDI (oppure SIMetrix/SIMPLIS Elements) per analizzare il comportamento di un filtro. Useremo inoltre uno strumento per progettare filtri passivi.
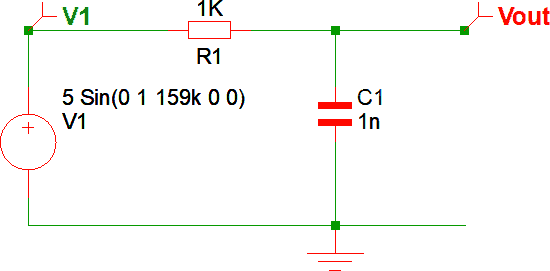
Disegnare il seguente circuito in MPLAB MINDI. Si tratta di un filtro passa basso (LPF) del primo ordine (nota 4). L'obbiettivo è disegnare la risposta in frequenza del filtro, cioè il grafico semilogaritmico che lega la frequenza con il guadagno in unità logaritmiche.
La frequenza di taglio può essere calcolata con la seguente formula, valida solo per i filtri RC del primo ordine:
fT = 1 / ( 2·π·C·R )
Prima di procedere è utile disegnare a mano l'andamento qualitativo della risposta in frequenza.
Simulare il circuito in modalità Transient e misurare la tensione efficace di ingresso (V1) e di uscita (Vout).
Escludere la parte iniziale del grafico in quanto i primi periodi sono diversi dagli altri.
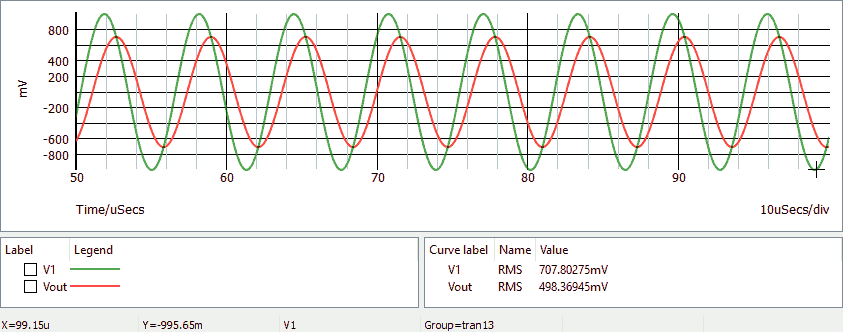
Le misure ed i calcoli devono essere inseriti in un foglio elettronico simile al seguente:

Usando il foglio elettronico rappresentare su grafico semilogaritmico i punti della tabella e confrontare tale grafico con la risposta in frequenza asintotica.
Descrivere cosa rappresenta e come leggere il grafico disegnato. Utilizzare gli stessi criteri richiesti per l'attività 5.
[ Avanzato ] Oltre al guadagno, misurare la fase ed inserire i valori trovati nel grafico semi-logaritmico del guadagno.
In questa attività esamineremo un HPF (nota 4) del primo ordine; esso è costituito da un resistore ed un condensatore scambiati di posizione rispetto al circuito dell'attività 1:
La formula da utilizzare per trovare la frequenza di taglio fT è la stessa vista nell'attività 1.
Procedere allo stesso modo descritto nella attività 1 e disegnare la funzione di trasferimento.
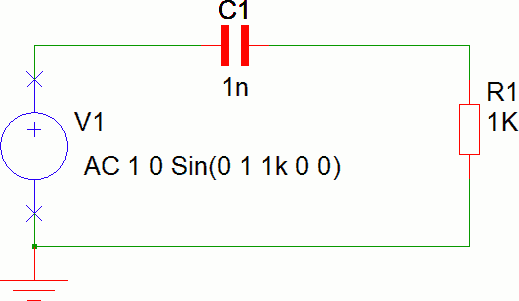
La risposta in frequenza di un filtro la la possiamo ottenere con una modalità molto più rapida di quanto visto nelle precedenti attività 1 e 2, attraverso la simulazione AC.
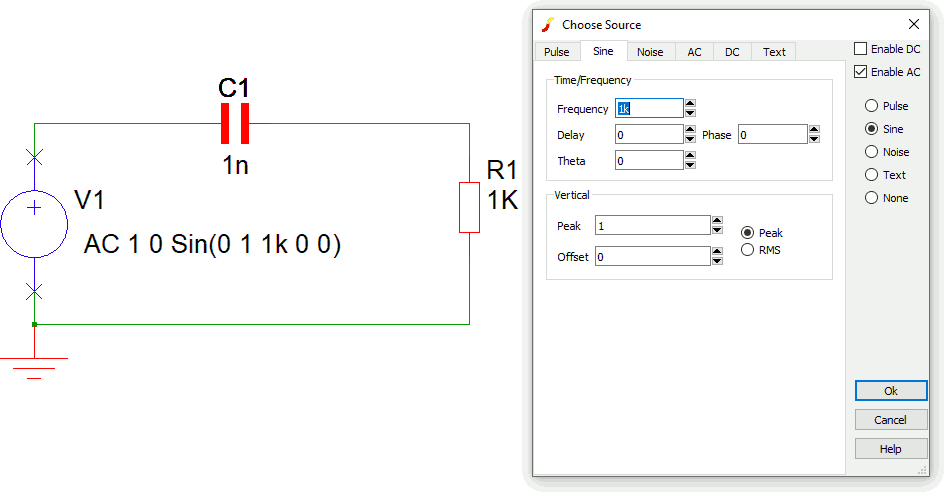
L'elemento più significativo per il generatore è il segno di spunta su Enable AC.
La simulazione va impostata in modalità AC, come di seguito mostrato. In particolare occorre impostare la frequenza minima e massima, indicativamente due decadi prima e due decadi dopo fT.
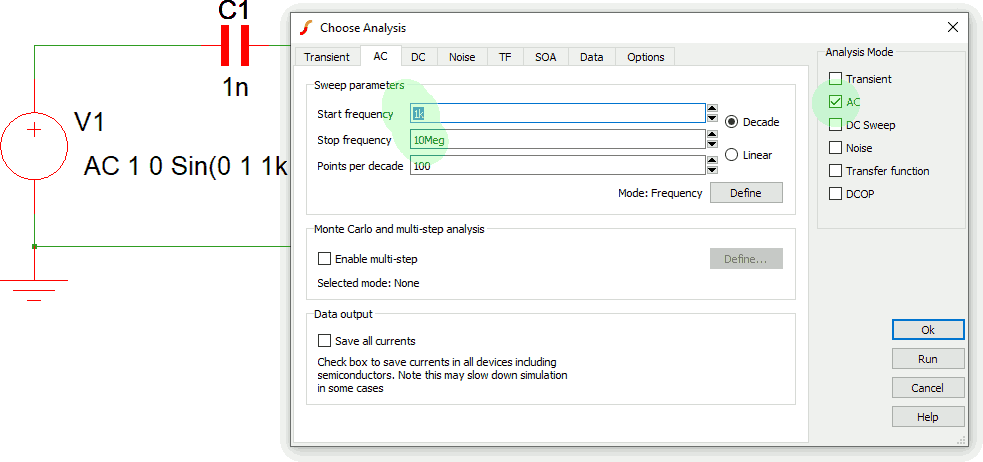
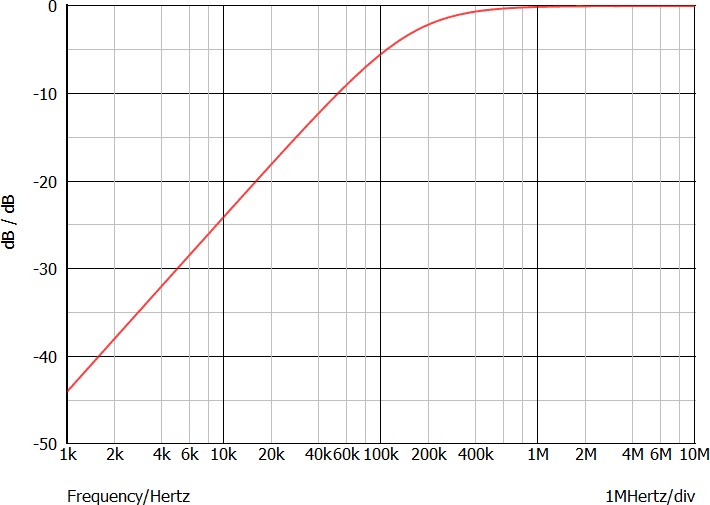
Occorre scegliere come sonda Probe AC/Noise → Fixed dB Probe ai capi di R1, l'uscita del quadripolo (nota 8).
[ Avanzato ] La sonda Probe AC/Noise → Fixed Phase Probe mostra come cambia la fase al cambiare della frequenza:
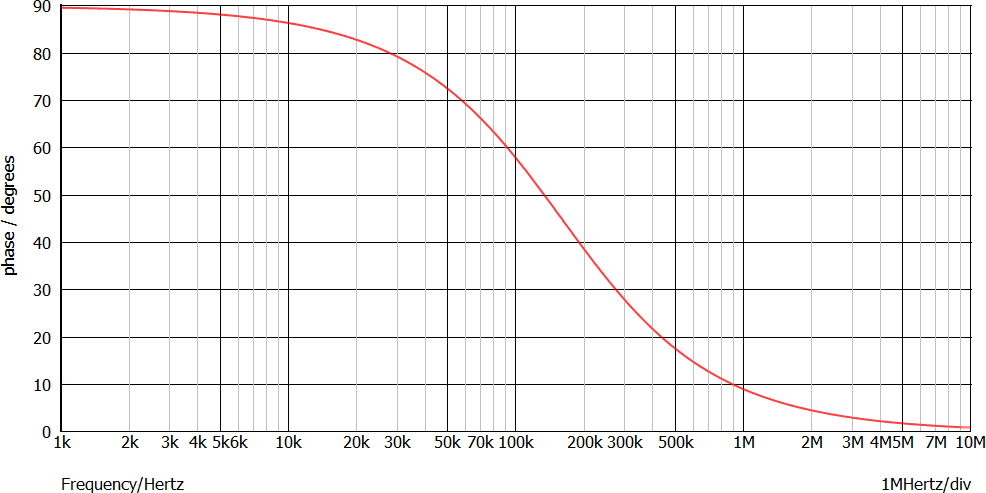
Essa varia tra 0° e 90°.
Convenzionalmente si dice che le frequenze superiori a 160 kHz "passano" all'uscita del filtro, frequenze inferiori "non passano".
Tale valore può essere definito, a seconda dei contesti e dei dati disponibili, in uno dei seguenti modi, tutti più o meno coincidenti dal punto di vista numerico:
Progettare un filtro passa alto del primo ordine con frequenza di taglio pari ad 1 MHz, utilizzando la formula riportata nell'attività 1 (nota 5).
Disegnare la risposta in frequenza senza far uso di un programma di simulazione (e neppure di un righello o un foglio a quadretti...). Come riferimento potete utilizzare questo esempio ed i seguenti.
Simulare il circuito con SIMetrix/SIMPLIS Elements in modalità Transient e disegnare la risposta in frequenza con Excel/Calc o altro foglio elettronico, come descritto nell'attività 1. Evidenziare la frequenza di taglio.
Simulare il circuito con SIMetrix/SIMPLIS Elements in modalità AC e visualizzare la risposta in frequenza, come descritto nell'attività 2bis; evidenziare la frequenza di taglio.
La progettazione di filtri di ordine superiore al primo è cosa spesso complessa. Una soluzione approssimata è quella di porre più filtri in cascata scegliendo per il secondo un valore di resistenza 10 volta maggiore, per il terzo 100 volte maggiore e così via. Occorre ovviamente cambiare di conseguenza il valore dei condensatori (nota 4).
Il seguente è un LPF del secondo ordine:
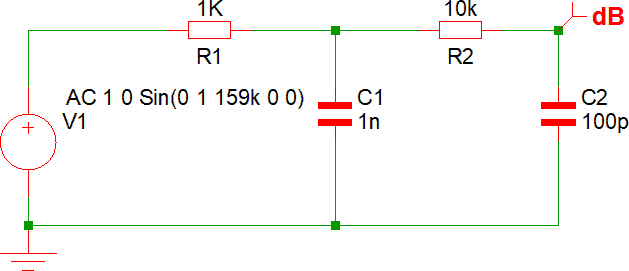
La stessa tecnica è utilizzabile anche, per esempio, per realizzare filtro passa banda:
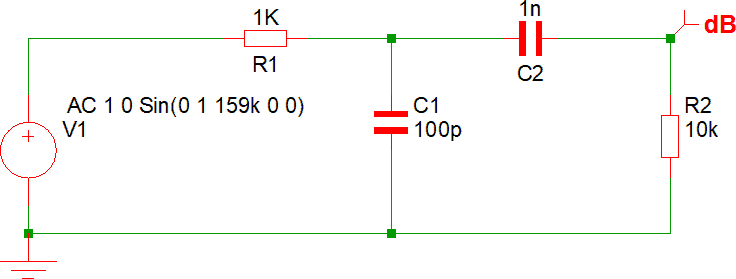
Utilizzando il sito https://markimicrowave.com/technical-resources/tools/lc-filter-design-too (oppure in alternativa https://rfdesigntools.pythonanywhere.com/tool/filter_design) per progettare un filtro con le seguenti caratteristiche:
In questo caso, a differenza delle precedenti attività, progetteremo un filtro adattato con impedenza caratteristica pari a 50 Ω.
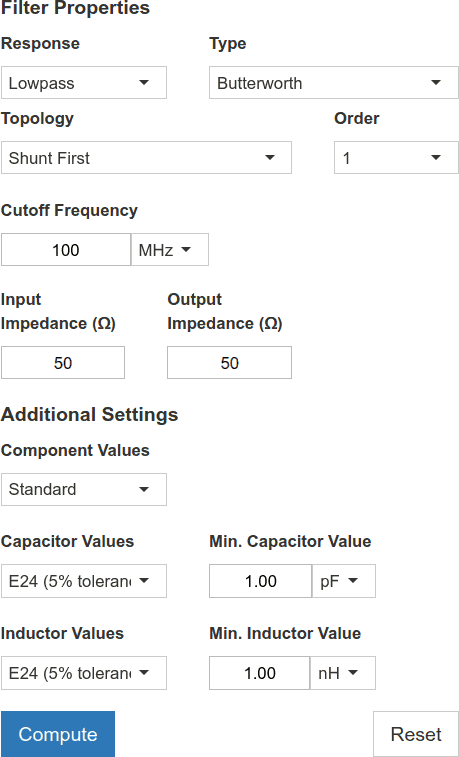
Disegnare il circuito con SIMetrix/SIMPLIS Elements e simularlo
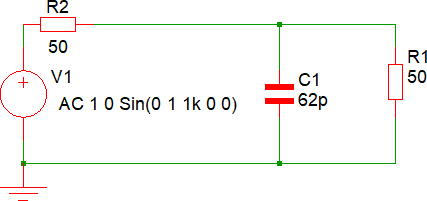
La risposta in frequenza risultante dovrebbe essere simile alla seguente:
Progettare un filtro con le stessa caratteristiche dell'attività 4, ma del secondo ordine.
Ripetere le stesse misure del punto precedente.
Progettare un filtro con le stessa caratteristiche dell'attività 4, ma del quarto ordine.
Ripetere le stesse misure dei punti precedenti.
Individuare come l'ordine del filtro è legato:
Porre in ingresso al filtro dell'attività 6 un segnale ad onda quadra con frequenza 100 MHz, con tensione compresa tra -1 V e +1 V.
Disegnare manualmente la risposta in frequenza asintotica del filtro, come già fatto nelle attività precedenti.
Simulare il filtro in modalità AC, come già fatto nelle attività precedenti.
Simulare (nota 7) il circuito in modalità Transient:
Progettare un filtro passa banda con banda passante compresa tra 2 MHz e 5 MHz del 4 ordine.
Disegnare manualmente la risposta in frequenza asintotica del filtro.
Simulare il filtro in modalità AC.
Considerare in ingresso un'onda quadra con frequenza 5 MHz, VH = 10 V, VL = 0 V. Simulare (nota 7) il circuito in modalità Transient e mostrare l'uscita sia nel dominio del tempo che in quello della frequenza.
Pagina creata nell'ottobre 2020.
Ultima modifica: 10 gennaio 2026
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)