Unità logaritmiche: esercizi

Home → Tutorial → Appunti scolastici → Quadripoli → Unità logaritmiche → Esercizi

Questa pagina contiene alcuni esercizi sulle unità logaritmiche. La descrizione teorica ed alcuni esempi possono essere trovati alla pagina Unità logaritmiche.

Attenzione agli "zeri" e alle unità di misura!

Esercizio 1

Potenze

Convertire le seguenti potenze da unità lineari ad unità logaritmiche:

100 W
3 mW
0,1 W
0,01 mW
2000 mW
0,04 mW
8 W
50 µW

[ 20 dBW (oppure 50 dBm); 4,8 dBm; 20 dBm; -20 dBm; 33 dBm; -14 dBm; 39 dBm; -13 dBm ]

Convertire le seguenti potenze da unità logaritmiche ad unità lineari:

20 dBm
-20 dBm
-23 dBm
5 dBW
12 dBm

Per controllare questi risultati, applicare le formule inverse.

Tensioni

Convertire le seguenti tensioni in unità logaritmiche (dBV):

3 V
-1 V
0,25 V
110 V
2 V

[ 9,5 dBV; 0 dBV; -12 dBV; 40,8 dBV; 6 dBV ]

Convertire le seguenti tensioni in unità lineari:

3 dBV
-5 dBV
10 dBV
100 dBµV

Per controllare questi risultati, applicare le formule inverse.

Varie...

Convertire le seguenti grandezze da lineari a logaritmiche

8 mW
10 V
10 mV
2 W
-3 V
10 µW

Convertire le seguenti grandezze da logaritmiche a lineari

7 dBm
-5 dBm
8 dBV
100 dBm
5 dBW
100 dBV
-6 dBV
0 dBµV
0 dBu

Per controllare questi risultati, applicare le formule inverse.

Esercizio 2

Date le seguenti tensioni sinusoidali in ingresso ed uscita ad un quadripolo:

Tensione di picco di ingresso: 10 mV
Tensione di picco di uscita: 3 V

Calcolare:

Guadagno di tensione (in unità lineari ed in unità logaritmiche)
Attenuazione di tensione (in dB e come numero puro)
Potenza di ingresso ed uscita, in unità lineari (tutte le resistenza sono uguali e pari a 75 Ω)
Potenza di ingresso ed uscita, in unità logaritmiche
Guadagno di potenza (in unità lineari ed in unità logaritmiche)
Attenuazione di potenza (in unità lineari ed in unità logaritmiche)

[ 49.5 dB; 300
-49.5; 0,003
661 nW; 60 mW
-31.8 dBm; 17,7 dBm
49.5 dB; 90 000
-49.5 dB; 1,1E-5 ]

Esercizio 3

Come il precedente esercizio:

Tensione efficace di ingresso: 40 mV
Tensione efficace di uscita: 1 V
Z₀ = 75 Ω

[ 28 dB; 25
-28 dB; 0,04
21 µW; 13 mW
-16,7 dBm; 11.2 dBm
28 dB; 625
-28 dB; 0.0016 ]

Esercizio 4

Un segnale è somma di tre sinusoidi:

1 V_RMS, 10 kHz
2 V_RMS, 30 kHz
1,5 V_RMS, 200 kHz

Disegnare su grafico semilogaritmico:

Lo spettro delle tensioni, in dBV
Lo spettro delle potenze, in dBm. Tutte le resistenze sono di 50 Ω

Soluzione

Esercizio 5

Con i dati dell'esempio 3, calcolare i guadagni di tensione e potenza, sia con unità lineari che logaritmiche.

Come posso verificare la coerenza di quanto qui trovato con i risultati dell'esempio 3?

[ 0,5; 0,25; -6 dB; -6 dB ]

Esercizio 6

Un amplificatore d'antenna adattato sia in ingresso che in uscita ha guadagno pari a 60 dB. Determinare quanto vale la potenza di uscita se la potenza in ingresso è pari a -70 dBm.

[ -10 dBm ]

Esercizio 7

Di seguito sono mostrate l'uscita (in rosso) e l'ingresso (in verde) di un quadripolo.

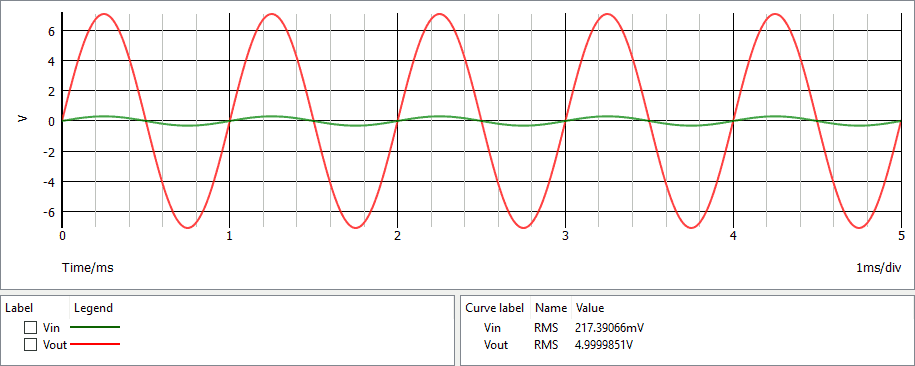
Due sinusoidi

Determinare:

La tensione efficace in ingresso ed uscita, in volt e dBV
La potenza in ingresso ed uscita, in mW e dBm. Tutte le impedenze sono uguali e valgono 100 Ω
Il guadagno di tensione, in unità lineari e logaritmiche
L'attenuazione di tensione, in unità lineari e logaritmiche
Il guadagno di potenza, in unità lineari e logaritmiche
L'attenuazione di potenza, in unità lineari e logaritmiche

Esercizio 8

Disegnare il grafico dell'esempio 4 su scala lineare, sia per la potenza che per frequenza.

Soluzione

Esercizio 9

Con i dati dell'esempio 2, calcolare le attenuazioni di tensione e potenza su scala lineare e logaritmica.

Come posso verificare tali risultati?

[ 0,002; -54 dB; 0.000004; -54 dB ]

Esercizio 10

Il guadagno di un quadripolo è pari a 20 dB. L'ingresso è costituito da tre sinusoidi con le seguenti caratteristiche:

f1 = 1 MHz, P1 = 10 dBm
f2 = 3 MHz, P2 = 20 dBm
f3 = 10 MHz, P2 = -10 dBm

Disegnare lo spettro di potenza del segnale di ingresso su grafico semilogaritmico
Disegnare lo spettro di potenza del segnale di uscita su grafico semilogaritmico

Soluzione (punto 2)

Esercizio 11

Il guadagno di un quadripolo, variabile con la frequenza, è descritto dal seguente grafico.

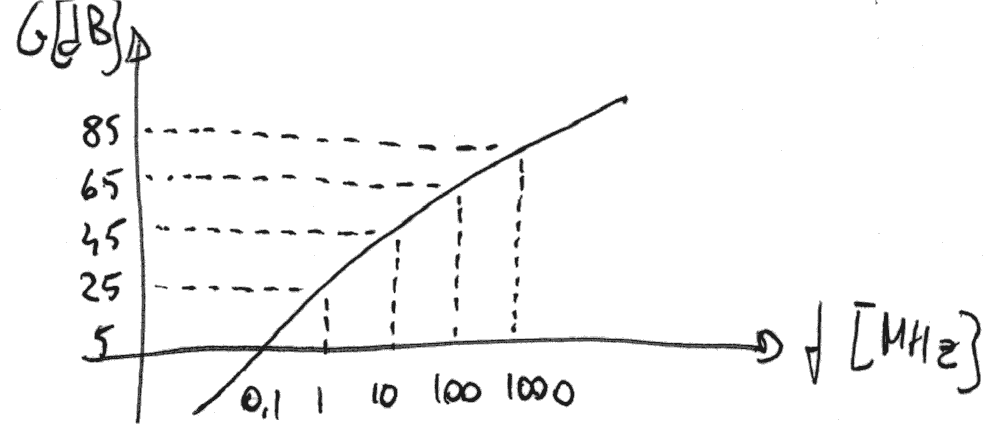
L'ingresso è costituito da tre sinusoidi con le seguenti caratteristiche:

f1 = 1 MHz, P1 = 10 dBm
f2 = 10 MHz, P2 = 20 dBm
f3 = 100 MHz, P2 = 0 dBm

Disegnare lo spettro di potenza del segnale di ingresso su grafico semilogaritmico
Disegnare lo spettro di potenza del segnale di uscita su grafico semilogaritmico

Soluzione (punto 2)

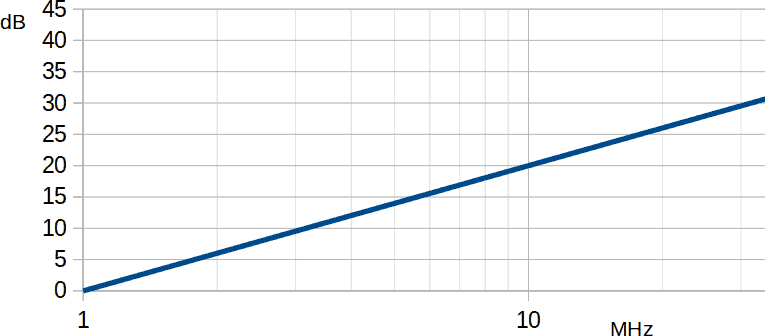
Esercizio 12

Il guadagno di un quadripolo, variabile con la frequenza, è descritto dal seguente grafico.

Esercizio 12

L'ingresso è costituito da un'onda quadra con ampiezza 5 V e frequenza 3 MHz,

Disegnare lo spettro di tensione del segnale di ingresso su grafico semilogaritmico
Disegnare lo spettro di tensione del segnale di uscita su grafico semilogaritmico

Soluzione (punto 2)

Pagina creata nel settembre 2022
Ultima modifica: 18 ottobre 2024