• Pagina principale
• Novità
• Tutorial
• Progetti
• Non solo elettronica
• Contatti
• Trova nel sito

Home → Tutorial → Appunti scolastici → Circuiti DC → Teorema di Thévenin → Esercizi

Il teorema di Thevenin è utile per semplificare circuiti complessi; per utilizzarlo occorre:

• Individuare il bipolo lineare a cui applicare il teorema, eventualmente togliendo parti del circuito originale. Questa operazione non è necessaria se il circuito da studiare è già sotto forma di bipolo
• calcolare la resistenza interna del generatore reale equivalente (R_EQ), vista dai terminali del bipolo dopo aver annullato i generatori indipendenti
• calcolare la tensione del generatore (V_EQ), pari alla tensione misurata a vuoto ai capi del bipolo.

Esempio 1 (bipolo)

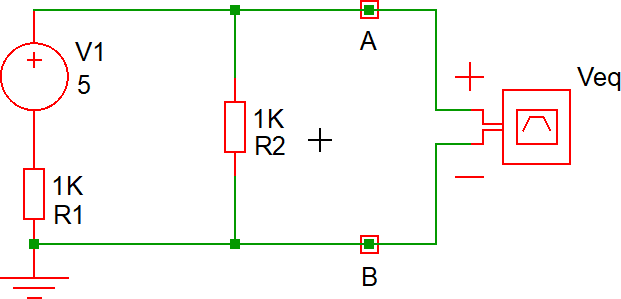
Dato il seguente bipolo, determinare il suo circuito equivalente secondo Thevenin.

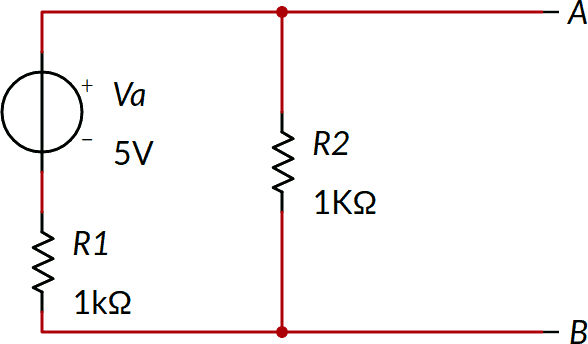
Il bipolo è lineare, quindi possiamo applicare il teorema di Thévenin.

Prima parte: VEQ

Occorre determinare la tensione tra i morsetti A e B nella situazione disegnata, cioè a vuoto. Tale tensione coincide con la tensione V2 ai capi di R2.

R1 ed R2 sono in serie in quanto attraversate dalla stessa corrente (nota 3):

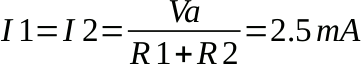
Troviamo la tensione ai capi di R2 con la legge di Ohm:

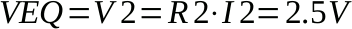
Alla stessa conclusione si poteva giungere più velocemente applicando la formula del partitore di tensione.

Seconda parte: REQ

Dopo aver annullato il generatore Va, il circuito diventa il seguente:

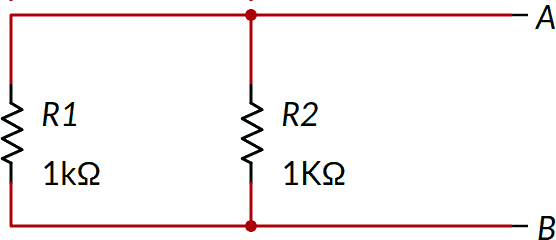
R1 ed R2 sono in parallelo (nota 2). REQ è pertanto di 500 Ω.

Conclusione

Il circuito equivalente secondo Thévenin di quello proposto è pertanto il seguente:

Qualunque circuito collegato ai morsetti A e B del circuito equivalente avrà esattamente lo stesso comportamento di uno collegato al circuito originario.

Verifica dei risultati

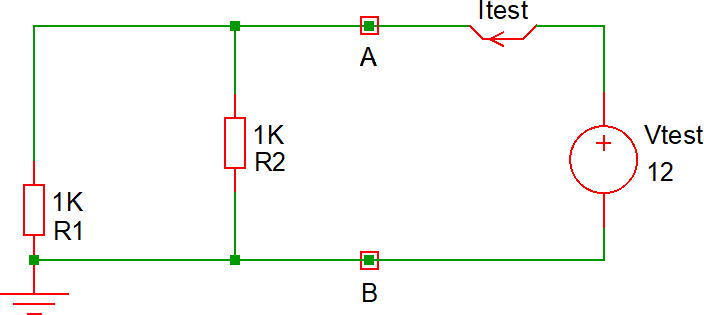
Per verificare la correttezza del risultato è possibile utilizzare un simulatore, applicando direttamente le definizioni. Quanto mostrato di seguito fa riferimento a SIMetrix/SIMPLIS Elements.

Per la misura della tensione equivalente VEQ è sufficiente collegare una sonda differenziale direttamente ai due morsetti A-B: la tensione letta è la VEQ ed ovviamente coincide con quanto sopra calcolato (2.5 V).

Più articolato trovare il valore della REQ. Occorre:

• Annullare tutti i generatori (nell'esempio vi è solo V1)
• Collegare tra i morsetti A-B un generatore di test che eroga una qualunque tensione (Vtest = 12 V nell'esempio seguente)
• Misurare la corrente Itest erogata dal generatore di test (24 mA nell'esempio seguente)
• Calcolare la REQ con la legge di Ohm: R = Vtest / Itest (nell'esempio: 500 Ω, valore ovviamente coincidente con quanto sopra calcolato)

Esempio 2 (bipolo)

Dato il seguente bipolo, determinare il suo circuito equivalente secondo Thevenin. 

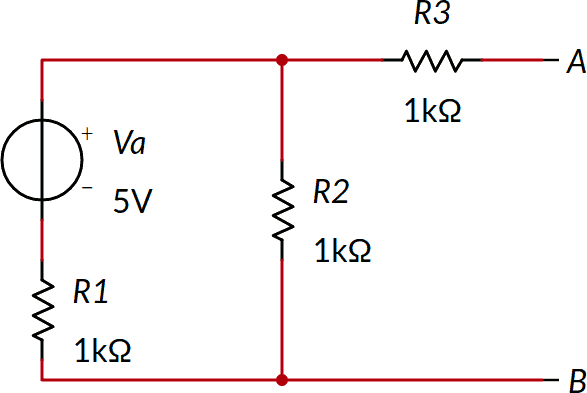
Il bipolo è lineare, quindi possiamo applicare il teorema di Thévenin.

Prima parte: VEQ

Occorre determinare la tensione ai morsetti A e B nella situazione disegnata, cioè a vuoto. Disegniamo il verso di tensioni (in blu) e correnti (in verde).

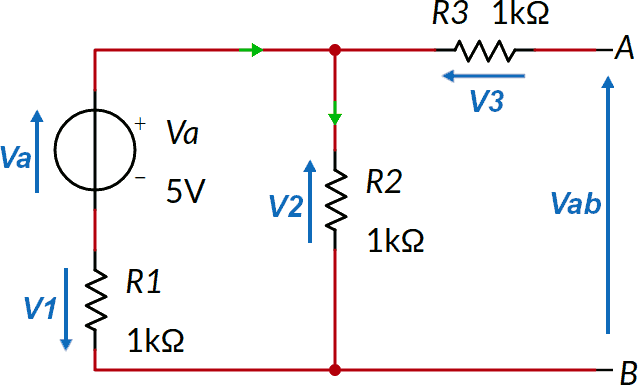
Scriviamo l'equazione di Kirchhoff alla maglia di sinistra.

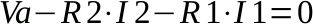
Le due correnti I1 e I2 sono uguali in quanto la corrente I3 è nulla perché il circuito è aperto, a vuoto, come richiesto dal teorema. Indichiamo tale corrente con I12, calcoliamola e calcoliamo V2 ai capi di R2:

 

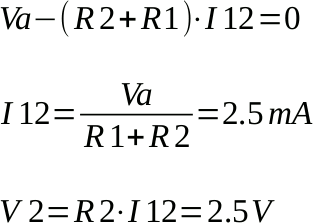
Scriviamo infine l'equazione alla maglia di destra:

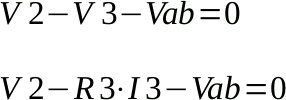
I3 è nulla, quindi Vab = V2 = 2,5 V (nota 3).

Seconda parte: REQ

Dopo l'eliminazione di Va, il circuito diventa il seguente:

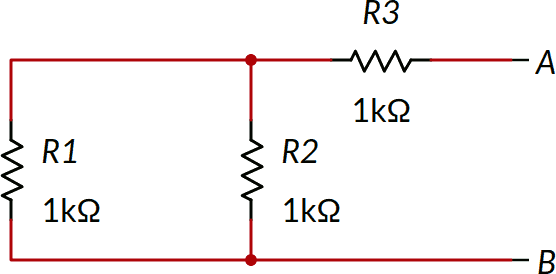
R1 è in parallelo a R2; quindi R12 = 500 Ω. R12 è in serie con R3 e quindi REQ è quindi pari a 1.5 KΩ.

Conclusione

Esempio 3 (bipolo)

Dato il seguente bipolo, determinare il suo circuito equivalente secondo Thevenin. 

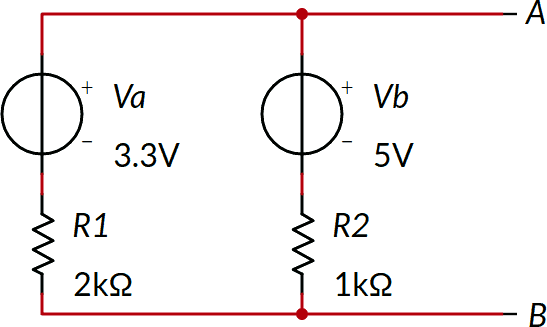
Il bipolo è lineare, quindi possiamo applicare il teorema di Thévenin.

Prima parte: VEQ

Useremo i principi di Kirchhoff. Indichiamo i versi di tensioni e correnti.

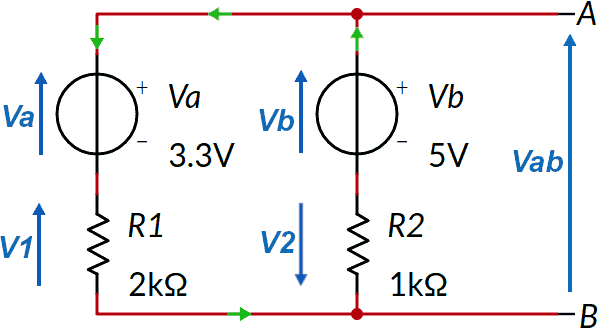
Alcune osservazioni:

• Nei due rami orizzontali collegati ai morsetti A e B non passa corrente (infatti sono a vuoto). Tutti i componenti sono quindi tra di loro in serie. Indicheremo semplicemente con I la corrente comune a tutti i componenti, in verde nel disegno. Il verso è arbitrario.
• Va e Vb hanno i versi derivanti dalla loro polarità. Si noti che Va non rispetta la convenzione dei generatori... Contrariamente alla prima impressione si tratta quindi di un utilizzatore, per esempio un accumulatore che si sta caricando (nota 4).

Scriviamo l'equazione alla maglia di sinistra e ricaviamo la corrente I:

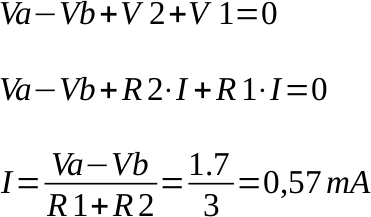
Troviamo Vab scrivendo l'equazione alla maglia di destra:

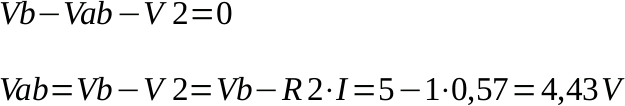
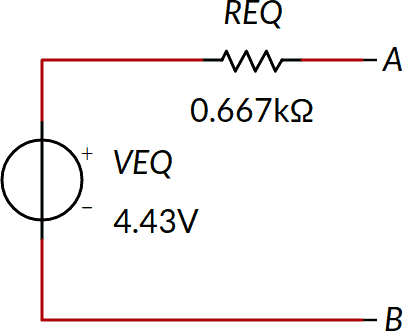
Quindi VEQ = 4,43 V.

Seconda parte: REQ

Dopo aver annullato i due generatori, R1 ed R2 sono in parallelo. Quindi REQ = 0.667 KΩ.

Conclusione

Il bipolo equivalente è il seguente:

Esempio 4 (circuito generico)

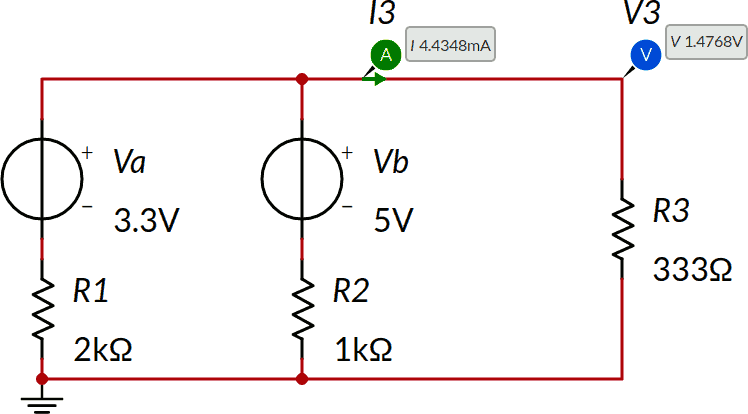
Consideriamo il seguente circuito e calcoliamo la tensione V3 ai capi di R3 e la corrispondente corrente I3. I risultati sono già mostrati nello schema.

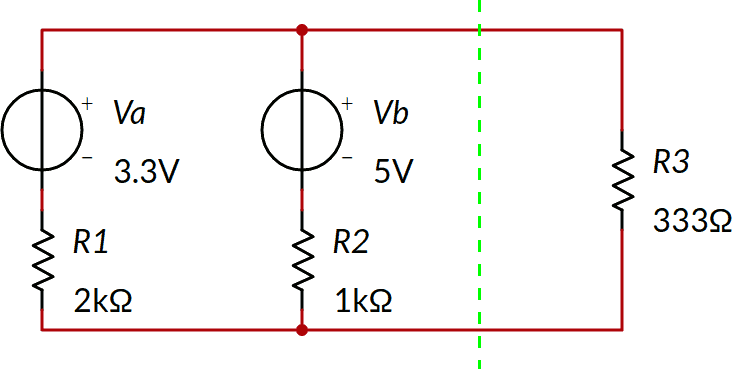
Non abbiamo un bipolo per il quale trovare il generatore reale equivalente agli effetti esterni. Possiamo però tagliare lungo la linea tratteggiata mostrata nello schema seguente ottenendo a sinistra un bipolo a cui applicheremo il teorema di Thevénin e a destra R3.

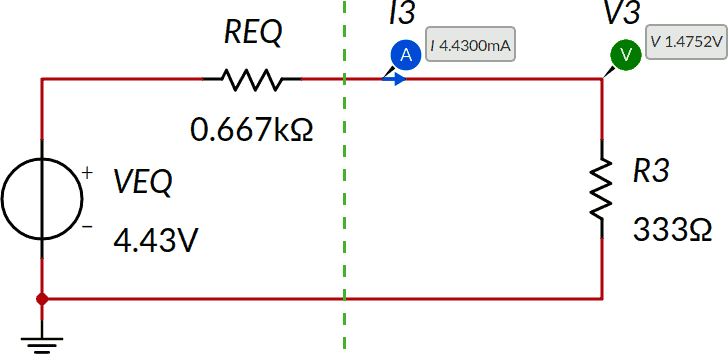
Il bipolo alla sinistra della linea tratteggiata è lineare, quindi possiamo applicare il teorema di Thévenin.

Il teorema di Thévenin afferma che la corrente in R3 (effetto esterno) non cambierà sostituendo il bipolo alla sinistra con il suo equivalente. Il bipolo equivalente è già stato calcolato nell'esempio 3. Di conseguenza il nuovo circuito è mostrato di seguito, con indicato I3 e V3, coincidenti con quanto proposto.

Esempio 5 (circuito generico)

Consideriamo il seguente circuito e calcoliamo la tensione VLED ai capi del LED e la corrispondente corrente ILED. I risultati sono già mostrati nello schema.

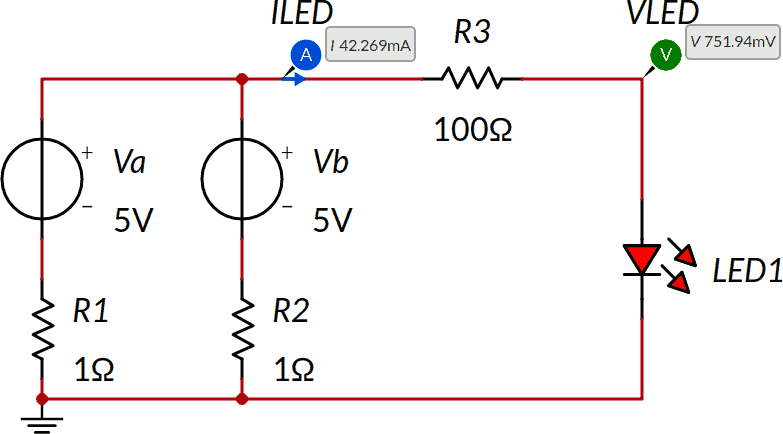
Non abbiamo un bipolo per il quale trovare il generatore reale equivalente agli effetti esterni. Possiamo però per esempio tagliare lungo la linea tratteggiata mostrata nello schema seguente ottenendo a sinistra un bipolo lineare e a destra il LED.

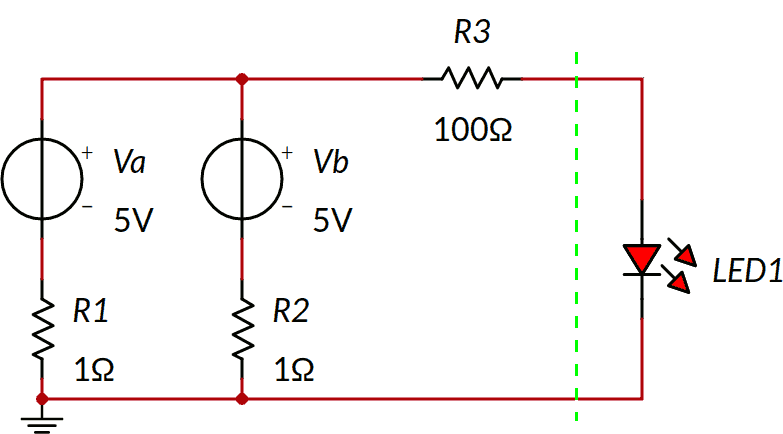
Il bipolo alla sinistra della linea tratteggiata è lineare, quindi possiamo applicare il teorema di Thévenin.

Si noti che il circuito sulla destra (il circuito esterno al bipolo) è costituito da un LED, elemento non lineare. Il teorema di Thevenin non richiede alcuna caratteristica speciale a tale circuito esterno, ma solo al bipolo che dovrà essere semplificato.

Il calcolo del bipolo equivalente è lasciato come esercizio. Di seguito il risultato e la verifica dell'equivalenza (nota 5)

Una soluzione alternativa

Per ricavare un bipolo si potrebbe in alternativa a quanto mostrato effettuare il "taglio" lungo la linea tratteggiata blu di seguito mostrata:

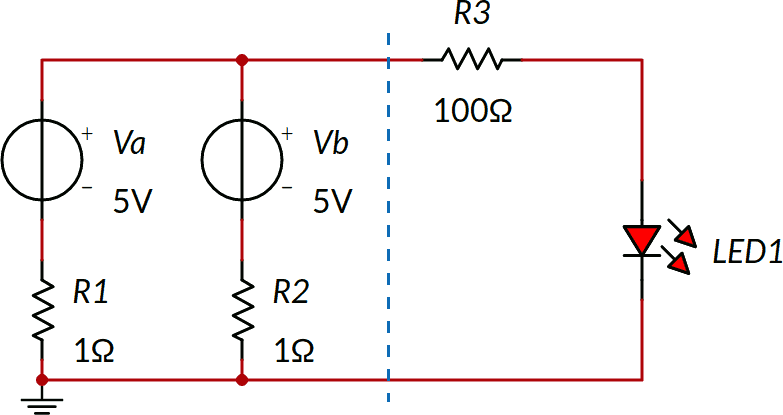
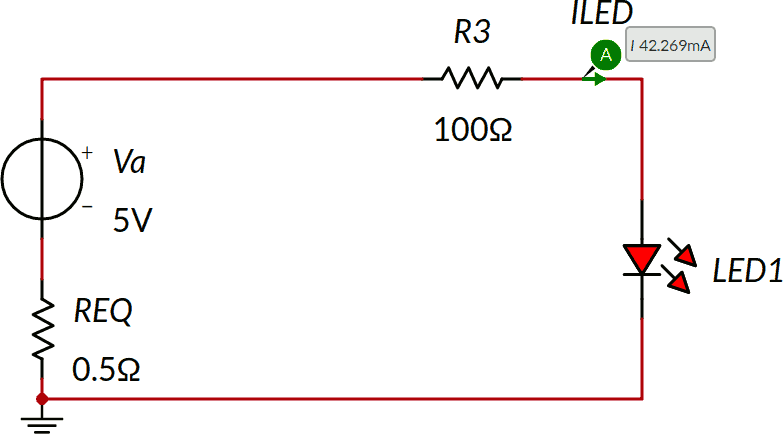
In questo caso il bipolo equivalente alla sinistra sarà costituito da VEQ = 5 V e REQ = 0,5 Ω (dimostrazione lasciata come esercizio).

Il circuito complessivo diventa di conseguenza quello di seguito mostrato, evidentemente equivalente per quanto riguarda ILED a quello precedentemente trovato.

Esercizio 6

Trovare il circuito equivalente secondo Thévenin del seguente bipolo:

 

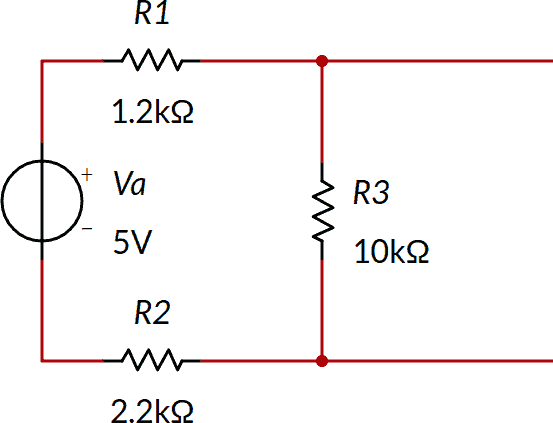
Collegare un resistore R4 da 5.6 kΩ tra i morsetti del bipolo equivalente e calcolare la tensione ai suoi capi.

Esercizio 7

Trovare il circuito equivalente secondo Thévenin del seguente bipolo (nota 6):

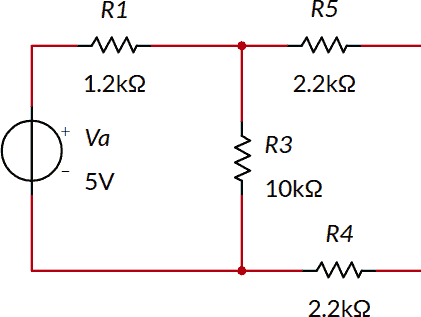
Collegare un resistore R6 tra i morsetti del bipolo equivalente. Fare variare il valore resistivo di R6 da 0 Ω a 10 kΩ e riportare su un grafico con i6 in ascissa e V6 in ordinata. Si consiglia vivamente l'uso di un foglio di calcolo...

Esercizio 8

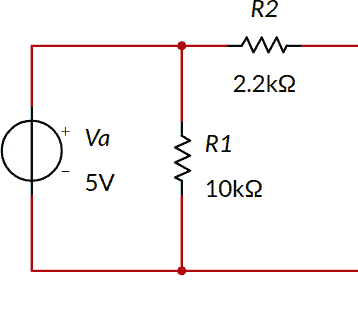
Trovare il circuito equivalente secondo Thévenin del seguente bipolo (nota 7):

Esercizio 9

Trovare il circuito equivalente secondo Thévenin del seguente bipolo (nota 9):

Esercizio 10

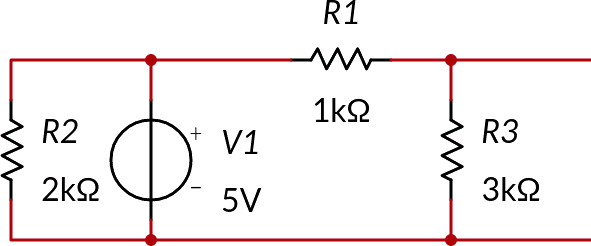
Dopo aver separato R2 dal resto del seguente circuito, trovare il bipolo equivalente al rimanente circuito (Va, Vb, R1, R3).

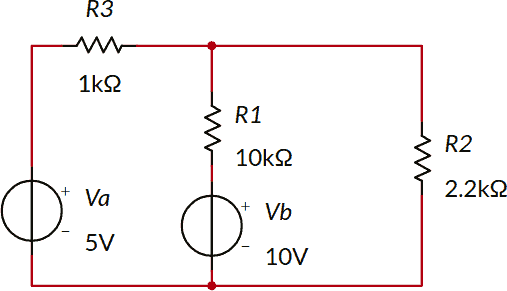
Trovare infine la corrente in R2, dopo averlo ricollegato al bipolo equivalente.

Esercizio 11

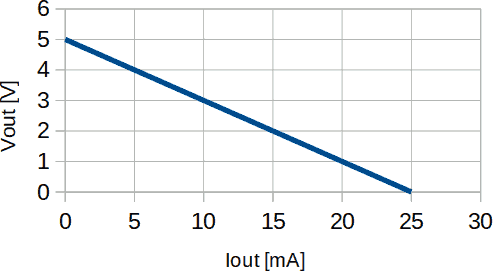
Il legame tra tensione e corrente per un bipolo lineare è rappresentato nel seguente grafico. Trovare VEQ ed REQ.

Esercizio 12

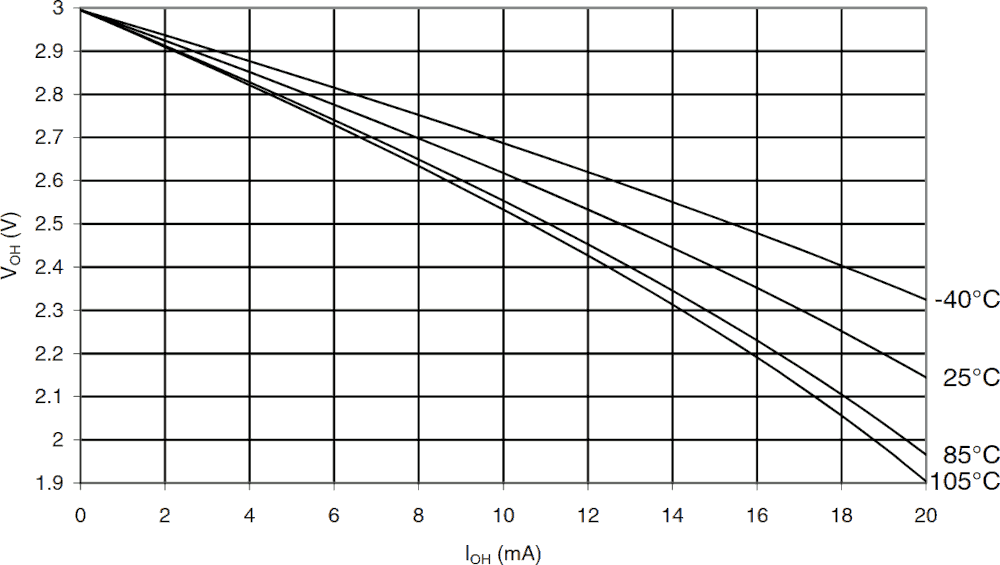
Il grafico seguente mostra la tensione e la corrente in uscita ad un circuito digitale con valore logico alto.

• Determinare la V_EQ e la R_EQ quando il valore logico è alto, alla temperatura di 25°C
• Determinare la V_EQ e la R_EQ quando il valore logico è alto, alla temperatura di 105°C

Esercizio 13

Disegnare il grafico che lega la tensione e la corrente ai capi di un generatore di tensione reale caratterizzato da:

• V_EQ = 10 V
• R_EQ = 100 Ω

 

Note

1. Il fatto che tra R1 ed R2 sia disegnato un nodo è irrilevante nell'affermare che siano in serie: verso destra non esce/entra nessuna corrente, essendo i morsetti A e B aperti (a vuoto) e quindi I2 = I1
2. Non si tratta di un errore! Questo circuito è infatti diverso dal precedente
3. Alla stessa conclusione si poteva arrivare osservando che, a vuoto, in R3 non passa corrente e quindi tale resistenza non influenza il funzionamento del circuito e, semplicemente, può essere tolta; il circuito risulta quindi identico a quello del primo esempio (solo relativamente al calcolo di VEQ!) e poteva quindi essere applicata la formula del partitore di tensione.
4. In realtà prima di fare questa affermazione dovremmo verificare di aver "indovinato" il verso della corrente
5. Non è qui presente il calcolo della corrente e della tensione, che richiede soluzioni grafiche, soluzioni approssimate oppure la soluzione di equazioni esponenziali
6. Il fatto che i resistori non attraversati da corrente non influiscano sulla VEQ è regola generale
7. Il fatto che i resistori in parallelo ai generatori di tensione ideali non influiscano sul funzionamento del circuito è regola generale

Data di creazione di questa pagina: novembre 2019
Ultima modifica: 10 ottobre 2023

---

Appunti scolastici - Versione 0.1025 - Maggio 2024
Copyright 2012-2024, Vincenzo Villa (https://www.vincenzov.net)

Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)