
Gustav Robert Georg Kirchhoff è stato un fisico prussiano del diciannovesimo secolo. In questa pagina sono descritte le due leggi che portano il suo nome, note come equazioni alle maglie ed equazioni ai nodi:
La somma algebrica delle tensioni lungo una maglia è pari a zero. Il verso di percorrenza della maglia è arbitrario come pure il punto di inizio. Le tensioni ai capi dei componenti che si attraversano percorrendo la maglia vanno sommate se concordi al verso di percorrenza, sottratte se discordi
La somma delle correnti entranti in un nodo è pari alla somma delle correnti uscenti (nota 8)
Tali leggi valgono per qualunque circuito in corrente continua (nota 2).
Consideriamo il seguente circuito, costituito da sei resistori e due generatori:
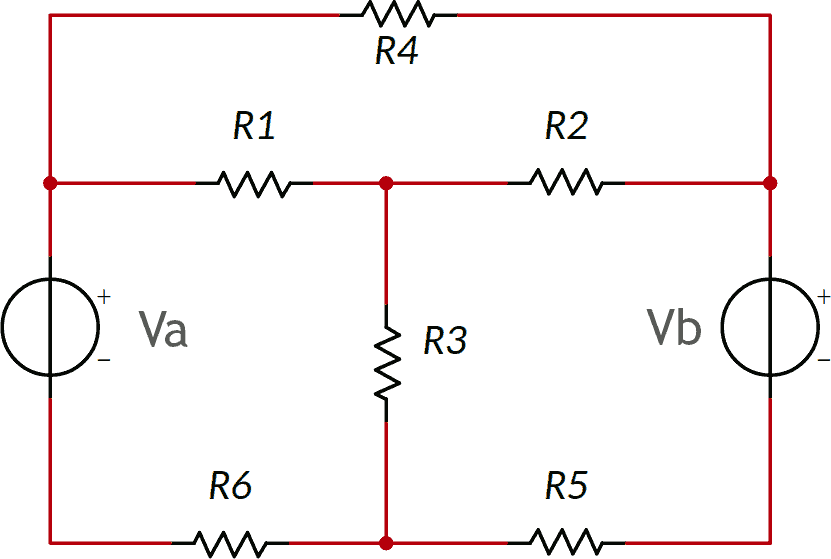
Per scrivere le equazioni di Kirchhoff occorre preliminarmente disegnare sullo schema le tensioni e le correnti presenti nel circuito e dare loro un nome, seguendo nell'ordine i seguenti passi:
Il risultato potrebbe essere simile al seguente, dove in blu abbiamo le tensioni ed in verde le correnti:
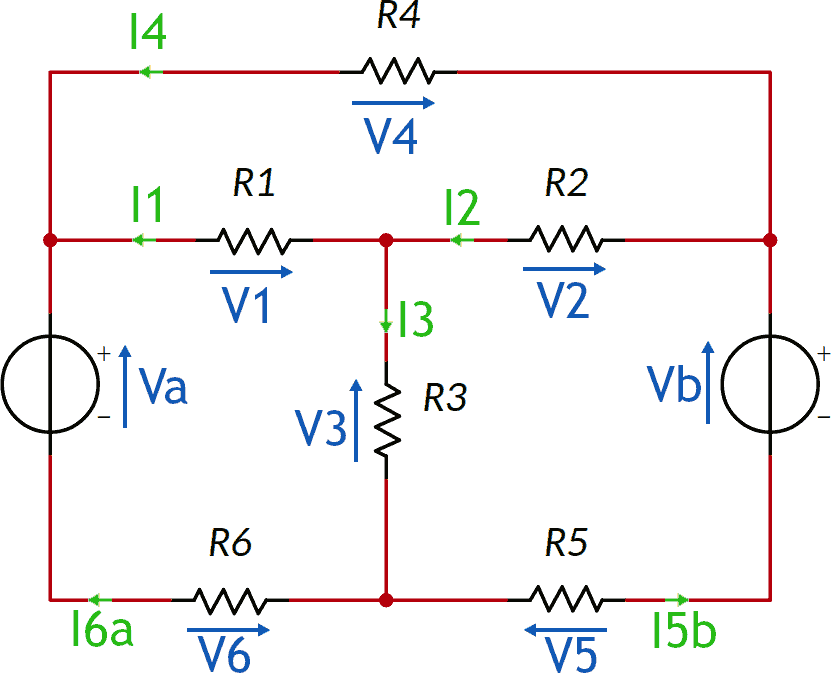
IMPORTANTE: quella disegnata NON è l'unica soluzione corretta in quanto molti versi sono stati scelti in modo arbitrario e quindi anche la scelta opposta è corretta!
A questo punto possiamo scrivere le equazioni ai nodi e alle maglie.
Nel circuito abbiamo quattro nodi. Scriviamo le equazioni ai nodi:
Nel circuito abbiamo molte maglie, forse sette (è inutile contarle...). Scriviamo le equazioni alle maglie:
In questo esempio useremo le equazioni di Kirchhoff per risolvere (nota 6) il seguente circuito; ovviamente in questo caso possiamo, più semplicemente, utilizzare la regola del partitore di tensione...
Troviamo nel seguente circuito la corrente e le due tensioni V1 e V2 ai capi di R1 ed R2
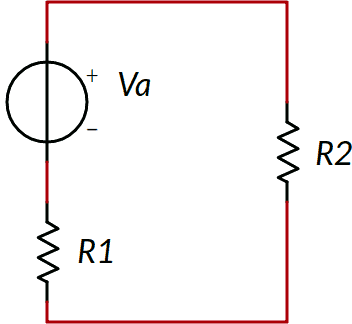
Come operazione preliminare occorre fare le stesse operazioni descritte nel precedente esempio:
Il circuito ottenuto è di seguito mostrato, con le tensioni indicate in azzurro e la corrente in verde. Per i nomi consiglio di fare scelte semplici e con cui è facile individuare errori, per esempio indicando la tensione con un nome che richiama quello del componente al quale si riferisce (per esempio V1 ai capi di R1).
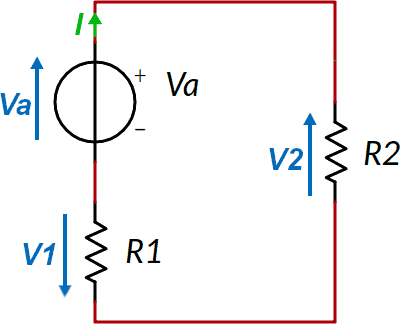
Possiamo scrivere l'equazione all'unica maglia. Occorre individuare un percorso, partendo da un punto arbitrario; muovendosi in un verso anch'esso arbitrario si sommano le tensioni incontrate se concordi al verso di percorrenza, si sottraggono se discordi. In questo esempio si è scelto come punto di partenza quello intermedio tra R1 e Va e come verso di percorrenza quello orario (nota 1):
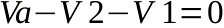
Per risolvere il circuito possiamo sostituire V1 e V2 con quanto ricavabile con la legge di Ohm (nota 3) e ricavare la corrente I:
I dati: R1 = R2 = 1 kΩ; Va = 10 V
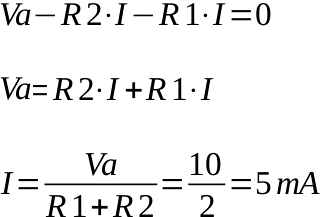
Infine utilizziamo la legge di Ohm, applicata ai due resistori, e trovare V1 = V2 = 5 V.
Consideriamo una porta logica NOT (inverter) a cui sono collegati un LED ed una resistenza. L'ingresso della porta logica è basso (L, zero logico), quindi l'uscita è alta (H, uno logico). Di seguito lo schema:
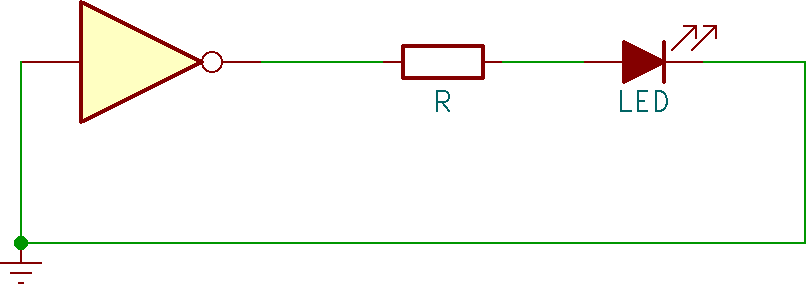
Come viene fatto normalmente, non è messo in evidenza alcun generatore di tensione anche se, per il funzionamento della porta, è richiesto il collegamento ad una alimentazione (VCC e GND).
Possiamo individuare la seguente maglia comprendente la porta logica, R ed il LED:
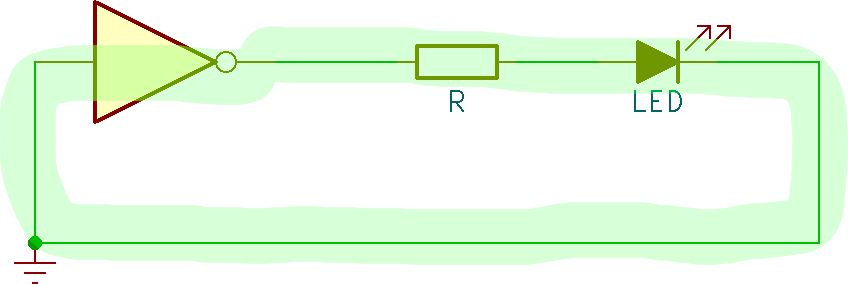
Disegniamo le tensioni e la corrente, facendo l'ipotesi che il LED sia acceso, cioè attraversato da corrente. Potrebbe sorgere qualche dubbio in merito al verso di VH: una porta logica è infatti un circuito complesso, difficile da classificare come generatore oppure utilizzatore (nota 7). Nel dubbio è sempre possibile mettere un verso arbitrario e verificare al temine di avere "indovinato".
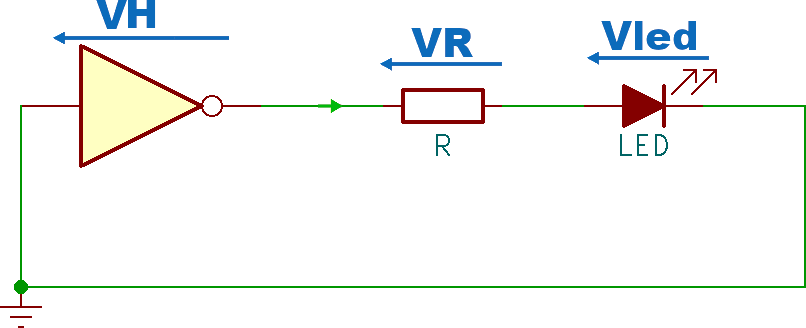
L'equazione alla maglia corrispondente è:
- VH - VR - Vled = 0
Si noti che il verso di VH non è stato scelto nel modo corretto; questo non è assolutamente un problema: semplicemente dai calcoli o dalle misure si scoprirà, al termine, che VH è una tensione negativa.
Si guardi inoltre all'esempio 6.
Consideriamo una porta logica a cui sono collegati un LED ed una resistenza. L'ingresso della porta logica è alto (H, uno logico), quindi l'uscita è bassa (L, zero logico). Di seguito lo schema:
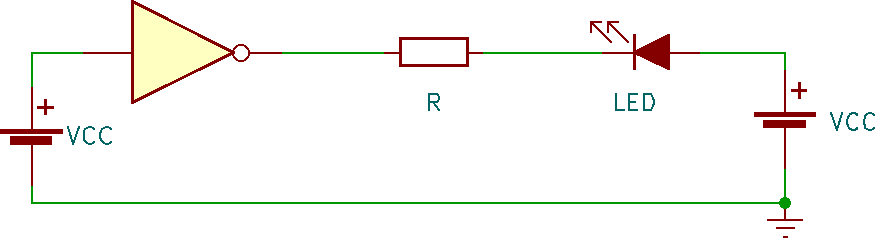
Spesso il circuito è disegnato diversamente, ma il significato rimane lo stesso:
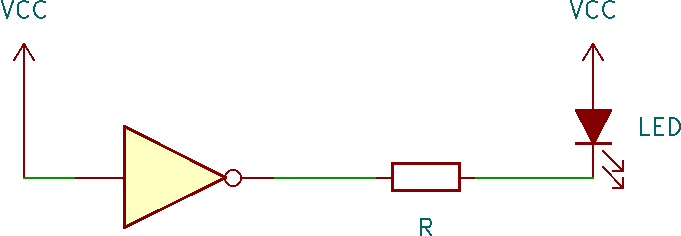
Individuiamo una maglia e disegniamo le tensioni e la corrente facendo l'ipotesi che il LED sia acceso, cioè attraversato da corrente. Potrebbe sorgere qualche dubbio sul verso di VL: una porta logica è infatti un circuito complesso, difficile da classificare come generatore oppure utilizzatore. Nel dubbio è sempre possibile mettere un verso arbitrario e verificare al temine dell'analisi di avere "indovinato".
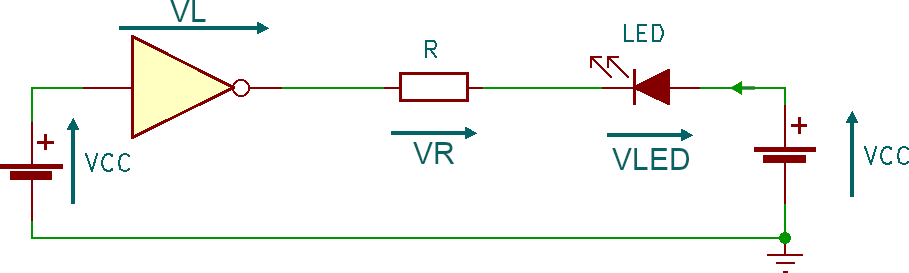
L'equazione alla maglia:
VCC + VL + VR + VLED - VCC = 0
SI noti che la tensione di alimentazione si "semplifica" e quindi non influenza il risultato finale.
Si guardi inoltre all'esempio 7.
Il principio di Kirchhoff alle maglie può essere riscritto considerando un qualunque percorso, aperto o chiuso, in cui il punto di partenza coincide con quello di arrivo:
L'obbiettivo è trovare la tensione tra i due morsetti AB.
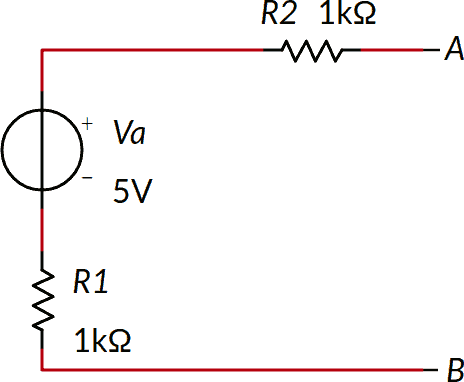
Siamo in presenza di una maglia aperta tra i due morsetti A e B; l'equazione alle maglie lungo il percorso di seguito evidenziato si scrive con gli stessi criteri già esposti.
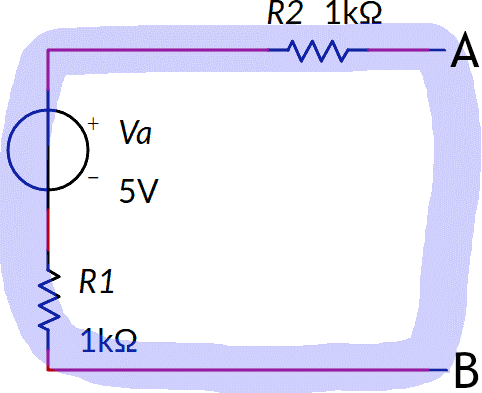
Disegnare sullo schema le tensioni e l'unica corrente, uscente dal polo positivo del generatore (in questo caso nulla), rispettando per i versi la convenzione di generatori e utilizzatori:
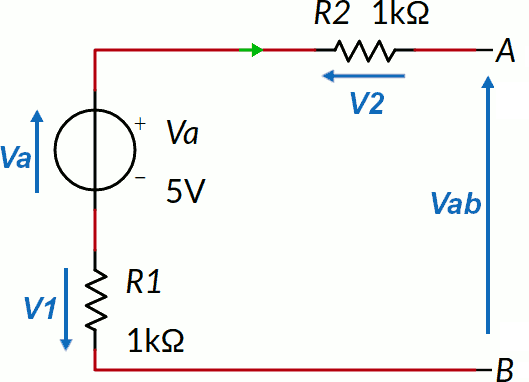
L'equazione è quindi:
Va - V2 - Vab - V1 = 0
Per risolvere il circuito possiamo:
Consideriamo il circuito mostrato nell'esempio 3. La maglia può essere ridisegnata considerando il circuito nel seguente modo:
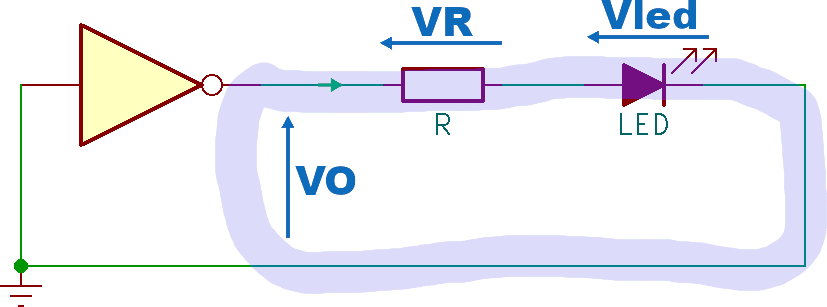
La tensione VO è quella presente tra la massa e l'uscita della porta logica e viene normalmente indicata come tensione di uscita della porta logica. A volte viene indicala come VOH per indicare che l'uscita (Out) si trova ad un livello logico alto (High).
L'equazione che ne deriva è:
VO - VR - Vled = 0
Consideriamo il circuito mostrato nell'esempio 4. La maglia può essere ridisegnata considerando il circuito nel seguente modo:
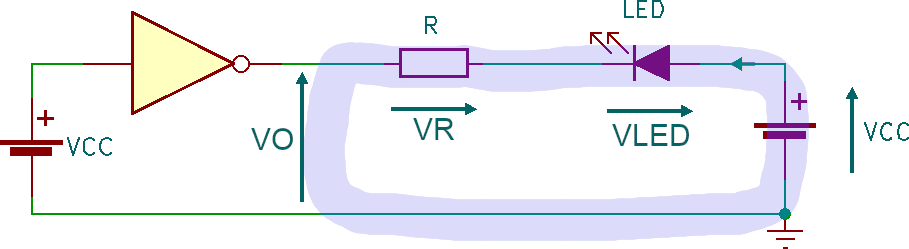
La tensione VO è quella presente tra la massa e l'uscita della porta logica e viene normalmente indicata come tensione di uscita della porta logica. A volte viene indicala come VOL per indicare che l'uscita (Out) si trova ad un livello logico basso (Low).
L'equazione che ne deriva è:
VO + VR + Vled - VCC = 0
Il principio di Kirchhoff ai nodi può essere riscritto considerando non un semplice nodo, ma una qualunque superficie chiusa che circonda una qualunque parte di un circuito:
In un certo senso possiamo affermare che una parte di circuito è diventata una "grande nodo" in cui entrano ed escono fili...
Nello stesso circuito dell'esempio 1 è evidenziata una superficie chiusa contenente tre resistori:
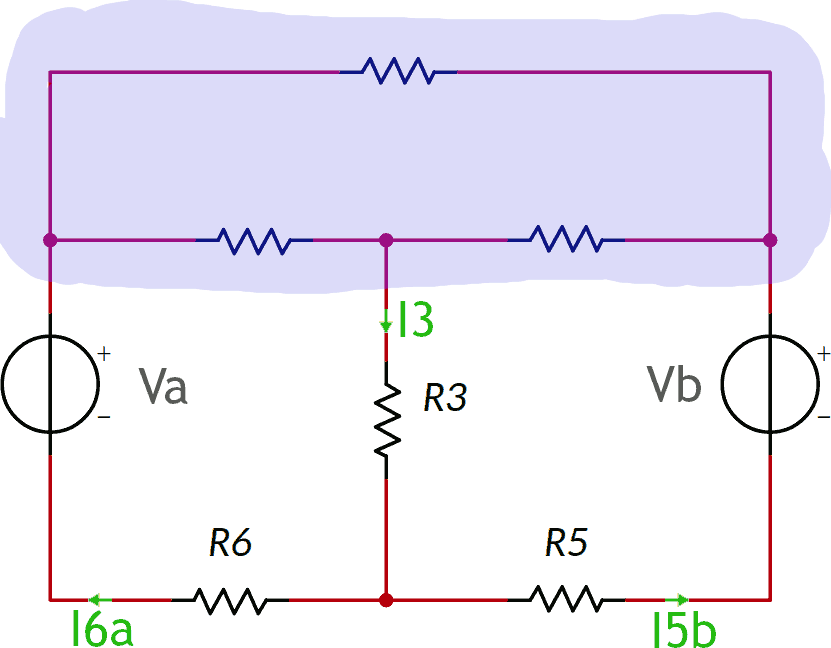
Il principio di Kirchhoff ai nodi afferma che:
I6a + I5b = I3
Il circuito integrato 74HC00 contiene quattro porte logiche NAND a due ingressi. Complessivamente ha 14 piedini, numerati da 1 a 14. Nello schema seguente è evidenziato dal rettangolo giallo; le frecce blu indicano il verso delle correnti: entrante per I14 perché collegato ad un generatore, arbitrario per i rimanenti 13 pin.
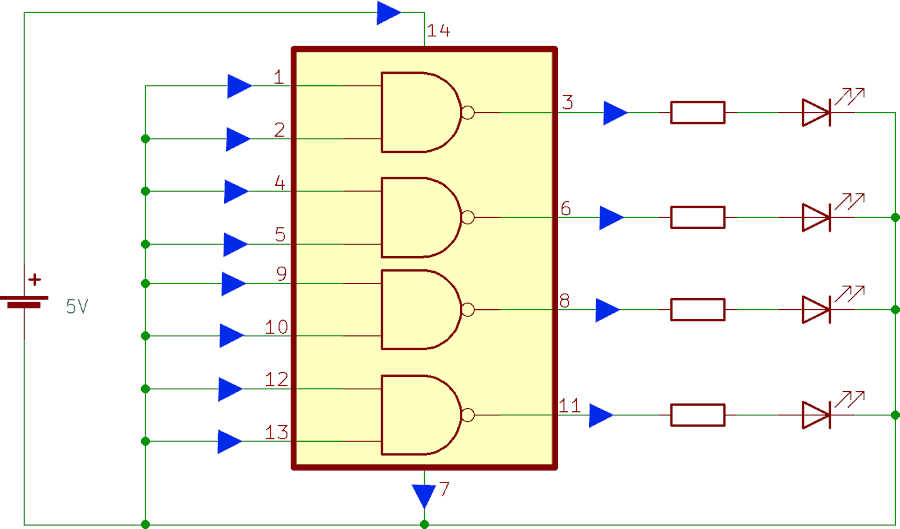
Possiamo scrivere il principio di Kirchhoff ai nodi nel seguente modo:
I14 + I1 + I2 + I4 + I5 + I9 + I10 + I12 + I13 = I3 + I6 + I8 + I11 + I7
I due principi di Kirchhoff valgono per qualunque circuito in corrente continua.
Se in un circuito non sono rispettati significa che stiamo dimenticando alcune parti dell'enunciato. Per esempio:
Questo circuito sembra mettere in difficoltà il principio di Kirchhoff alle maglie:
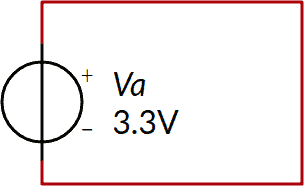
Se scriviamo l'equazione alla maglia otteniamo infatti
3.3 V = 0
cosa evidentemente non possibile.
Questa apparente contraddizione viene meno considerando che non esistono generatori ideali, ma solo generatori reali, caratterizzati da una resistenza in serie, "dimenticata" nello schema.
Il circuito seguente mostra una porta logica NOT la cui corrente di uscita Iout accende un LED.
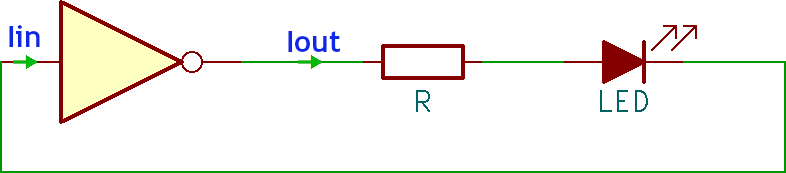
Non ci sono nodi in cui la corrente si dirama e quindi:
Iout = In
Effettuando una misura in laboratorio oppure leggendo i fogli tecnici si scopre che la corrente di ingresso della porta logica Iin è praticamente nulla; la corrente Iout nel LED acceso è invece pari a svariati mA. Evidentemente l'equazione scritta poco sopra non è corretta!
Questa apparente contraddizione viene meno considerando che la porta logica possiede anche due pin di alimentazione, da cui entra o esce corrente!
Data di creazione di questa pagina: novembre 2019
Ultima modifica: 24 ottobre 2025
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)