
La descrizione dei termini e dei concetti qui utilizzati è alla pagina Segnale sinusoidale, da studiare prima e consultare facendo gli esercizi.
Come per tutte le attività che richiedono risultati quantitativi è indispensabile indicare sempre:
Nel fare i grafici non è necessario né l'uso di software, né del "righello". Ovviamente è sempre presente un'approssimazione, ma è opportuno cercare di rispettare le scale.
Un segnale sinusoidale ha ampiezza massima 10 Vp, frequenza 50 Hz e fase nulla.
La pulsazione è ω = 2·π·50 = 314 rad/s.
La funzione matematica che descrive il segnale è quindi:
v(t) = 10 · sin (314 · t)
Il periodo è T = 1 / 50 = 20 ms.
Nel disegnare il grafico è opportuno non indicare troppi valori numerici, per non complicarne la lettura. Per esempio è sufficiente indicare il valore di picco della tensione (VP = 10 V) e il periodo (20 ms) o poco più:
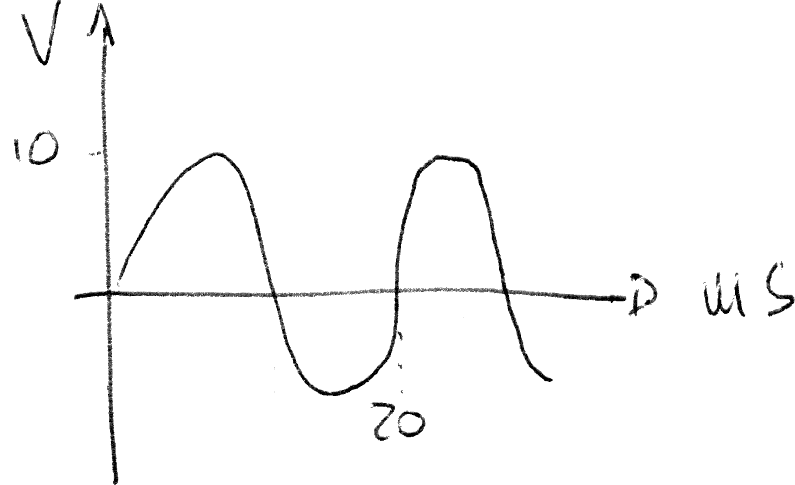
Si noti che il grafico della sinusoide inizia nell'origine degli assi essendo nulla la fase.
Immediato il disegno dello spettro: una singola linea verticale in corrispondenza di 50 Hz con lunghezza 10 V (se si vuole rappresentare il valore di picco, come qui mostrato) oppure 7,07 V (VRMS = Vp / √2 se si vuole rappresentare il valore efficace).
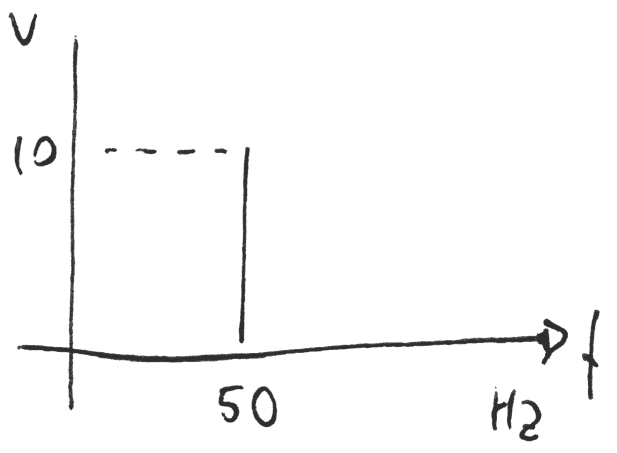
Lo stesso grafico può essere usato anche con unità logaritmiche: la lunghezza della linea sarà pari a VdBV = 20 log(10) = 20 dBV (valore di picco) oppure VdBV = 20 log(7,07) = 17 dBV (valore efficace).
Se si utilizza la rappresentazione semplificata descritta in queste pagine, nello spettro non vi è nessun riferimento alla fase.
Immediata anche la rappresentazione vettoriale: una linea orizzontale (o un punto) che parte dall'origine con lunghezza 10 VP (oppure 7,07 VRMS se vogliamo rappresentare la tensione efficace); su entrambi gli assi sono indicate tensioni.

In questo tipo di grafico non appare nessuna informazione relativa alla frequenza.
Un segnale sinusoidale ha ampiezza massima 10 V, frequenza 50 Hz e fase -45°. Rispetto all'esempio 1 è cambiata solo la fase.
La fase espressa in radianti è φ = -π/4 = -0,78 rad.
La funzione matematica che descrive il segnale è quindi:
v(t) = 10 · sin (314 · t - 0.78)
La fase è negativa e minore di 90°, quindi la sinusoide è in ritardo ("inizia" dopo l'origine degli assi). Una strada per visualizzarlo: disegnare prima il fasore ed affiancarlo al grafico nel dominio del tempo, come qui mostrato.
Per quantificare il tempo di ritardo TD possiamo considerare che 45° sono un ottavo di angolo, cioè un ottavo del periodo della sinusoide, cioè TD = 20 / 8 = 2.5 ms. In alternativa possiamo usare una delle formule che legano il ritardo TD e fase φ.
Nel grafico è sufficiente indicare il valore di picco della tensione (VP = 10 V), il periodo (20 ms) ed il ritardo (TD = 2.5 ms):
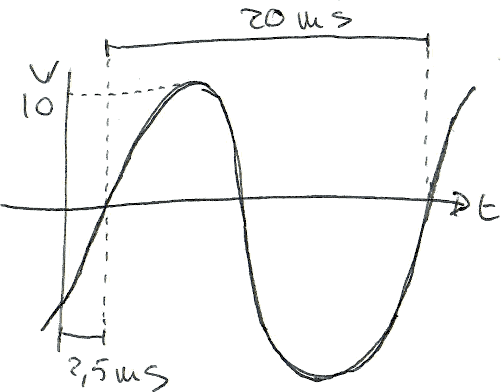
(non richiesto...) Per verificare numericamente il grafico possiamo, per esempio, calcolare la tensione per t = 2.5 ms e verificare che sia effettivamente 0 V:
v(2.5·10-3) = 10 · sin (314 · 2.5·10-3 - 0.78) = 0 V
Immediato il disegno dello spettro: è identico a quello mostrato nell'esempio 1.
Immediata anche la rappresentazione vettoriale (fasore): una freccia che parte dall'origine, inclinata di -45° (quindi verso il basso) e lunghezza 10 V:
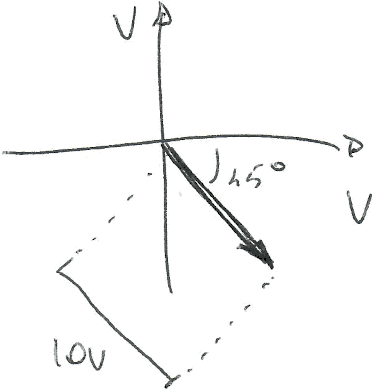
Potrebbe essere utile mettere in evidenza la proiezione del vettore sull'asse X e sull'asse Y oppure indicare un punto invece di un vettore:
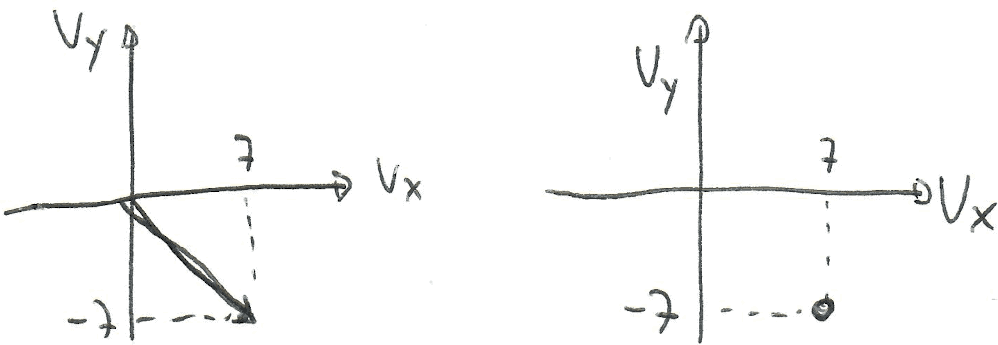
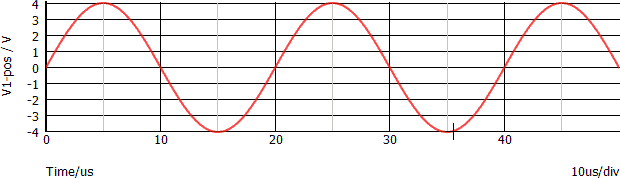
Si consideri la seguente sinusoide:
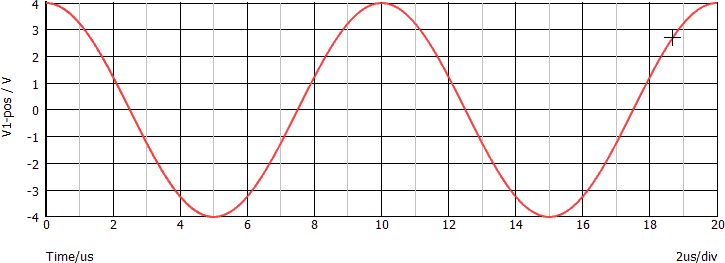
Si consideri la seguente sinusoide:
Disegnare il grafico (nel dominio del tempo e nel dominio della frequenza), la rappresentazione vettoriale e scrivere la funzione della seguente sinusoide:
Date le seguenti due sinusoidi:
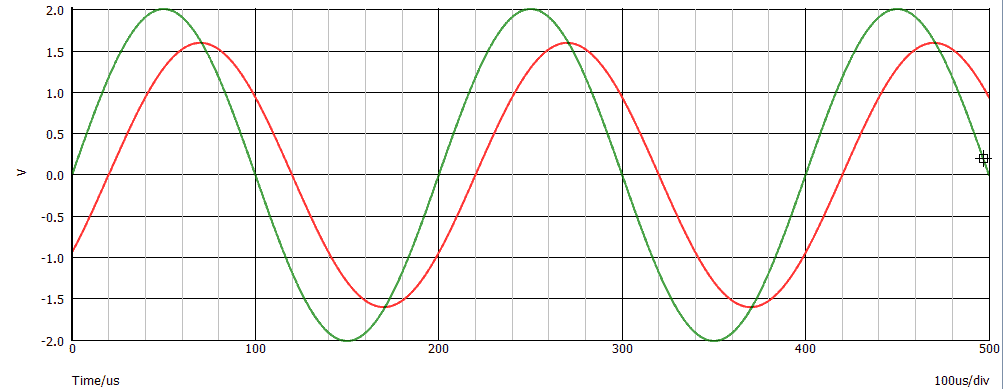
Relativamente agli ultimi due punti, possiamo utilizzare la proporzione che ci permette di trovare il modulo della fase:
0,2 / 360° = 0,02 / φ → φ = 0,02 · 360 / 0,2
Possiamo leggere sul grafico che il periodo è di circa 0,2 ms (= 200 µs) e che tra le due sinusoidi è presente un ritardo di circa 0,02 ms (= 20 µs); applicando la formula: |φ| = 36°.
Allo stesso risultato si poteva arrivare più velocemente applicando la stessa formula, ma misurando i tempi in "quadretti" invece che in secondi:
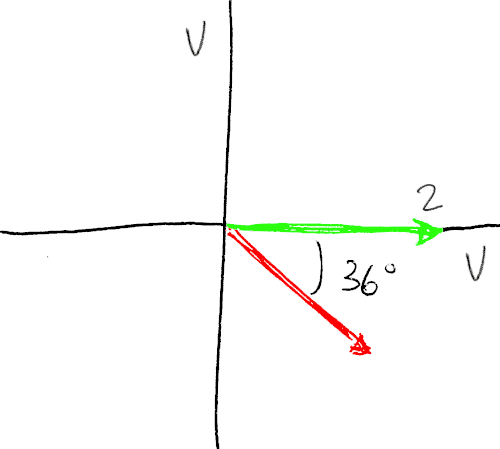
Il diagramma vettoriale delle due sinusoidi evidenzia lo sfasamento di 36° tra le sinusoidi. Il fasore "rosso" è leggermente più corto di quello "verde" e arriva dopo.
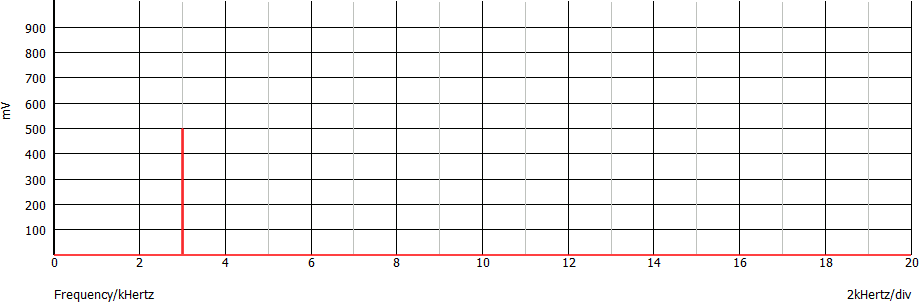
Dato il seguente spettro, relativo alla tensione picco:
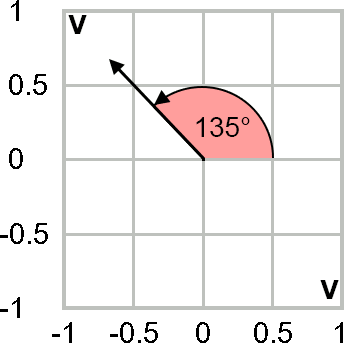
Un segnale sinusoidale con frequenza 2 MHz ha la seguente rappresentazione vettoriale relativa alla tensione di picco:
Creative Commons CC0 1.0 Universal Public Domain Dedication. https://commons.wikimedia.org/wiki - La palestra di Roper, Filadelfia, circa 1831
Data di creazione di questa pagina: aprile 2023
Ultima modifica: 4 ottobre 2025
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)