

Progettare un circuito combinatorio significa realizzare una rete di porte logiche il cui comportamento è conforme ad una descrizione data a parole ed in termini umani o, più formalmente, ad una tabella di verità.
Sono necessari tre passaggi:
Vogliamo realizzare un circuito combinatorio con due ingressi digitali A e B ed un'uscita Q. Q è alta quando entrambi gli ingressi sono uguali, bassa in caso contrario.
Creiamo la tabella di verità che corrisponde alla descrizione. In giallo sono indicati gli ingressi, con le 22 righe possibili; in azzurro è indicata l'uscita corrispondente alla descrizione:
| A | B | Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Si definisce mintermine il prodotto (nota 3) delle variabili di ingresso prese in forma normale (A) se valgono 1, prese in forma negata (A) se valgono 0. A volte è indicato con la lettera m minuscola. La tabella seguente, relativa ad una rete con due ingressi, mostra i quattro mintermini:
| A | B | m |
| 0 | 0 | A · B |
| 0 | 1 | A · B |
| 1 | 0 | A · B |
| 1 | 1 | A · B |
Per il passaggio dalla tabella di verità all'espressione booleana occorre:
| A | B | Q | ||
| 0 | 0 | 1 | ← | A · B |
| 0 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 1 | ← | A · B |
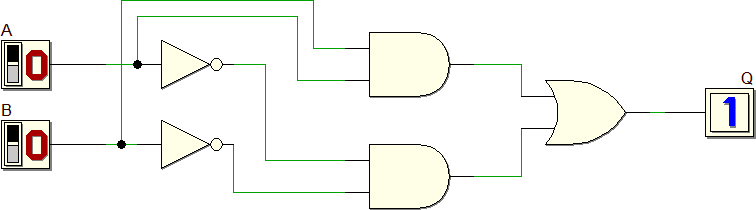
Q = (A · B) + (A · B)
Tale espressione viene chiamata Prima Forma Canonica oppure Forma Canonica SP (somma di prodotti).
La Prima Forma Canonica è l'espressione duale della Seconda Forma Canonica (nota 2) e viceversa, ovviamente.
Si definisce maxtermine la somma (nota 3) delle variabili di ingresso prese in forma normale (A) se valgono 0, prese in forma negata (A) se valgono 1. A volte è indicato con la lettera M maiuscola. La tabella seguente è relativa ad una rete con due ingressi e mostra i quattro maxtermini:
| A | B | M |
| 0 | 0 | A + B |
| 0 | 1 | A + B |
| 1 | 0 | A + B |
| 1 | 1 | A + B |
Per il passaggio dalla tabella di verità all'espressione booleana occorre:
| A | B | Q | ||
| 0 | 0 | 1 | ||
| 0 | 1 | 0 | ← | A + B |
| 1 | 0 | 0 | ← | A + B |
| 1 | 1 | 1 |
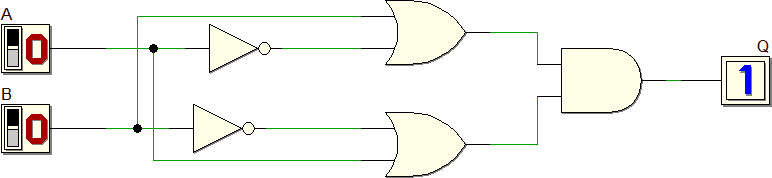
Q = (A + B) · (A + B)
Tale espressione viene chiamata Seconda Forma Canonica oppure Forma Canonica PS (prodotto di somme).
La Seconda Forma Canonica è l'espressione duale della Prima Forma Canonica (nota 2) e viceversa, ovviamente.
Le due forme canoniche sono ovviamente diverse come pure sono diversi i due circuiti. Il comportamento è però identico (nota 4).
Nei circuiti complessi è possibile scrivere direttamente il codice VHDL che descrive la tabella di verità e lasciare al software di sintesi l'onere di trovare la rete. Di seguito un esempio, sempre relativo a questa tabella di verità. L'ingresso è un array di due elementi
library IEEE;
use IEEE.std_logic_1164.all;
entity COMPARATORE is
port (
I : in std_logic_vector (1 downto 0;
Q : out std_logic);
end entity COMPARATORE ;
architecture RTL of COMPARATORE is
begin
with I select
Q <= '1' when '00',
'1' when '11',
'0' when others;
end architecture RTL;
Vogliamo realizzare un circuito combinatorio che somma aritmeticamente tre numeri di un bit ciascuno:
Creiamo la tabella di verità che corrisponde alla descrizione:
Per scrivere velocemente tutte le otto combinazioni degli ingressi A, B e C sono possibili due tecniche:
L'ordine delle righe non ha particolare importanza, anche se è utile per evitare confusione, dimenticanze o righe duplicate (nota 1).
La tabella, non ancora completata:
| A | B | C | MSB | LSB |
| 0 | 0 | 0 | ||
| 0 | 0 | 1 | ||
| 0 | 1 | 0 | ||
| 0 | 1 | 1 | ||
| 1 | 0 | 0 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 | ||
| 1 | 1 | 1 |
Possiamo quindi scrivere il valore delle uscite, leggendo la descrizione data a parole. L'ultima colonna, la somma in decimale, è stata inserita solo per chiarezza:
| A | B | C | MSB | LSB | |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 2 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 2 |
| 1 | 1 | 0 | 1 | 0 | 2 |
| 1 | 1 | 1 | 1 | 1 | 3 |
Se preferiamo, possiamo leggere la tabella precedente come costituita da due tabelle, ciascuna con una sola uscita:
| A | B | C | MSB |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| A | B | C | LSB |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Si definisce mintermine il prodotto (nota 3) delle variabili di ingresso prese in forma normale (A) se valgono 1, prese in forma negata (A) se valgono 0. A volte è indicato con la lettera m minuscola. La tabella seguente, relativa ad una rete con tre ingressi, mostra gli otto mintermini:
| A | B | C | m |
| 0 | 0 | 0 | A · B · C |
| 0 | 0 | 1 | A · B · C |
| 0 | 1 | 0 | A · B · C |
| 0 | 1 | 1 | A · B · C |
| 1 | 0 | 0 | A · B · C |
| 1 | 0 | 1 | A · B · C |
| 1 | 1 | 0 | A · B · C |
| 1 | 1 | 1 | A · B · C |
Per il passaggio dalla tabella di verità all'espressione booleana occorre:
| A | B | C | MSB | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 1 | ← | A · B · C |
| 1 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | ← | A · B · C |
| 1 | 1 | 0 | 1 | ← | A · B · C |
| 1 | 1 | 1 | 1 | ← | A · B · C |
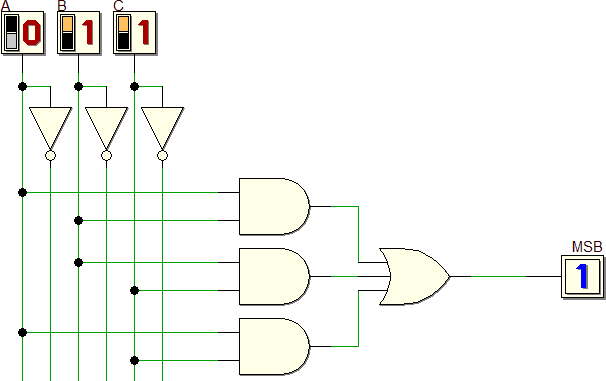
MSB = (A·B·C) + (A·B·C) + (A·B·C) + (A·B·C)
Tale espressione algebrica viene chiamata Prima Forma Canonica oppure Forma Canonica SP (somma di prodotti). La rete elettrica corrispondente a tale espressione è costituita dalla prima parte dello schema riportato più sotto.
La Prima Forma Canonica è l'espressione duale della Seconda Forma Canonica (nota 2) e viceversa, ovviamente.
La scrittura della prima forma canonica relativa a LSB è lasciata come esercizio. L'espressione algebrica e lo schema corrispondente è riportato nell'immagine riportata più sotto.
Si definisce maxtermine la somma (nota 3) delle variabili di ingresso prese in forma normale (A) se valgono 0, prese in forma negata (A) se valgono 1. A volte è indicato con la lettera M maiuscola. La tabella seguente, relativa ad una rete con tre ingressi, mostra gli otto maxtermini:
| A | B | C | M |
| 0 | 0 | 0 | A + B + C |
| 0 | 0 | 1 | A + B + C |
| 0 | 1 | 0 | A + B + C |
| 0 | 1 | 1 | A + B + C |
| 1 | 0 | 0 | A + B + C |
| 1 | 0 | 1 | A + B + C |
| 1 | 1 | 0 | A + B + C |
| 1 | 1 | 1 | A + B + C |
Per il passaggio dalla tabella di verità all'espressione booleana occorre:
| A | B | C | MSB | ||
| 0 | 0 | 0 | 0 | ← | A + B + C |
| 0 | 0 | 1 | 0 | ← | A + B + C |
| 0 | 1 | 0 | 0 | ← | A + B + C |
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | ← | A + B + C |
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 1 |
MSB = (A+B+C) · (A+B+C) · (A+B+C) · (A+B+C)
Tale espressione viene chiamata Seconda Forma Canonica oppure Forma Canonica PS (prodotto di somme).
La Seconda Forma Canonica è l'espressione duale della Prima Forma Canonica (nota 2) e viceversa, ovviamente.
L'ultimo passaggio è il disegno della rete a partire da una qualunque delle due forme canoniche (nota 4); in genere conviene scegliere la più piccola, se esiste. Nel caso di questo esempio è indifferente (il numero di 1 coincide con il numero di 0) e viene mostrata la rete completa ottenuta con la Prima Forma Canonica:
Il codice per la sintesi VHDL:
library IEEE;
use IEEE.std_logic_1164.all;
entity SOMMA is
port (
I : in std_logic_vector (2 downto 0;
MSB : out std_logic);
LSB : out std_logic);
end entity SOMMA ;
architecture RTL of SOMMA is
begin
with I select
MSB <= '1' when '011',
'1' when '101',
'1' when '110',
'1' when '111',
'0' when others;
with I select
LSB <= '1' when '001',
'1' when '010',
'1' when '100',
'1' when '111',
'0' when others;
end architecture RTL;
A volte l'uscita di una tabella di verità può non avere importanza, cioè vale indifferentemente 1 oppure 0. In tal caso l'uscita si indica con una X. Questo avviene tipicamente quando una certa combinazione di ingressi non può esistere: in tal caso è inutile indicare 1 oppure 0.
Nello scrivere la forma canonica, si considera la X come 1 oppure 0 a seconda di cosa è più conveniente. In pratica nello scrivere la prima forma canonica si considerano le X come 0; nello scrivere la seconda forma canonica si considerano la X come 1.
La seguente tabella indica il comportamento di fronte ad un semaforo: F=1 indica che l'auto deve fermarsi, F=0 indica che non bisogna fermarsi. Gli ingressi R, G e V indicano quali lampade sono accese.
Ovviamente se il semaforo funziona correttamente è accesa una sola lampadina alla volta:
La tabella corrispondente è la seguente:
| R | G | V | F |
| 0 | 0 | 0 | X |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | X |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | X |
| 1 | 1 | 0 | X |
| 1 | 1 | 1 | X |
Per scrivere la prima forma canonica, conviene considerare tutte le X=0:
F = (R·G·V) + (R·G·V)
Per scrivere la seconda forma canonica, conviene invece considerare tutte le X=1:
F = R + G + V
In questo caso le due forme canoniche NON sono più equivalenti
L'uso delle forme canoniche ha diversi vantaggi:
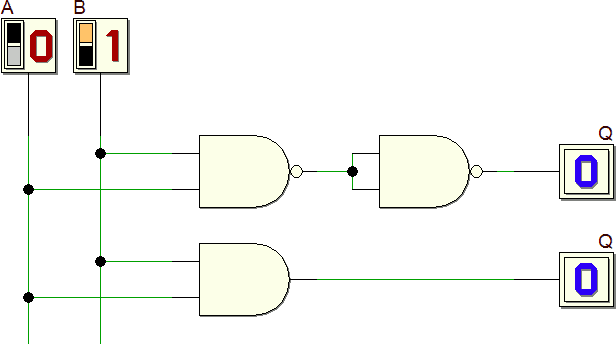
Ha lo svantaggio importante che il circuito prodotto è piuttosto grande (molte porte con molti ingressi). Per esempio, anche intuitivamente, è facile verificare che il seguente circuito produce lo stesso risultato della prima parte della rete progettata al punto precedente pur usando meno porte ciascuna delle quali ha meno ingressi:
Svariati sono i metodi che permettono di ottenere reti logiche ottimali, nessuno dei quali verrà qui spiegato:
Pagina creata nel settembre 2020
Ultima modifica: 7 febbraio 2023
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)