
Utilizzando circuito MSI, decoder e multiplexer in particolare, è possibile progettare reti combinatorie anche di una certa complessità. In questa pagina vedremo con due semplici esempi come procedere e successivamente come questi concetti sono impiegati in circuiti combinatori programmabili.
Il funzionamento del decoder è descritto in questa pagina. La sua struttura interna è la seguente, riferita ad un decoder da 2 a 4 senza enable:
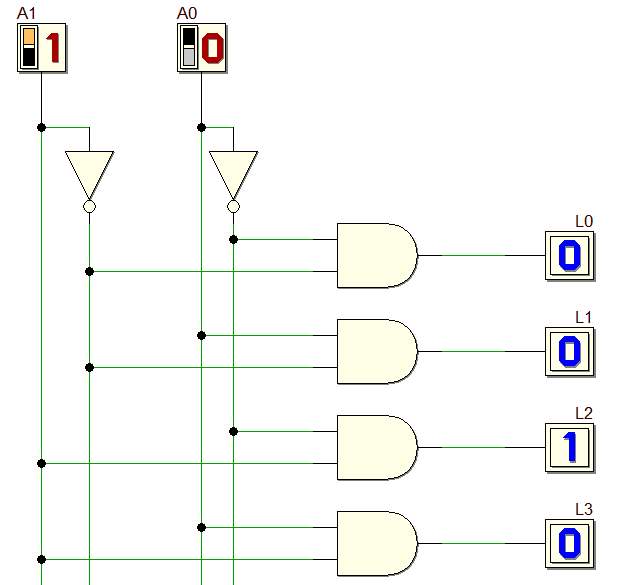
Confrontando tale struttura a quella ottenuta dalla prima forma canonica si osserva una notevole analogia: manca semplicemente la porta OR che collega le uscite delle AND corrispondenti ai mintermini per i quali l'uscita vale 1 per ottenere lo stesso circuito.
Realizziamo il circuito corrispondente alla seguente tabella di verità usando un decoder:
| A | B | C | Q |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Nello scrivere la tabella di verità è necessario:
Per realizzare il circuito è necessario utilizzare un decoder con tre ingressi (e quindi 8 uscite) perché tre sono le variabili di ingresso della tabella di verità.
Di seguito la soluzione: gli ingressi della porta OR sono collegati alle uscite 3 (011), 5 (101), 6 (110) e 7 (111) del decoder, cioè quelle corrispondenti agli "1" nella tabella di verità.
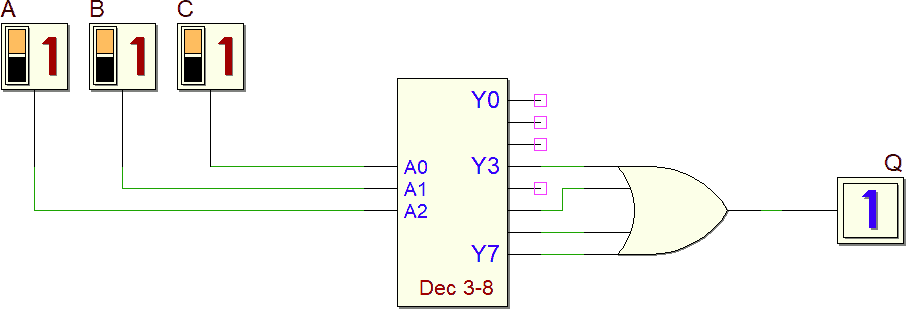
Nello schema precedente non è disegnato l'eventuale Enable; se presente deve essere opportunamente collegato per permettere il funzionamento del decoder.
Disegnare la rete corrispondente alla seguente tabella usando un decoder:
| A | B | C | Q |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Per verificare la corretta esecuzione dell'esercizio utilizzare un simulatore digitale come Deeds.
La struttura appena descritta in genere non è in genere utilizzata per realizzare circuiti combinatori usando singoli circuiti integrati, ma costituisce la base per realizzare Programmable Logic Array o simili dispositivi, antenati dei moderni CPLD.
Di seguito una parte semplificata di un vecchio circuito integrato programmabile PAL16L8:

Il produttore vende il componente senza alcun collegamento elettrico tra le righe e le colonne (nota 1); è l'utilizzatore che effettua la programmazione del componente creando gli opportuni collegamenti.
I multiplexer sono utilizzati per la sintesi di una tabella di verità, spezzandola in sottotabelle più piccole e quindi più facili da realizzare. Tali sottotabelle devono contenere un numero di righe potenze di due e devono avere tutte la stessa dimensione.
Consideriamo la seguente tabella. Per fare la sintesi dividiamo la tabella in quattro sottotabelle, ciascuna formata da due righe.
| A | B | C | Q |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| A | B | C | Q | |
| 0 | 0 | 0 | 0 | Q = 0 |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | Q = C |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | Q = C |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | Q = 1 |
| 1 | 1 | 1 | 1 |
Utilizziamo un multiplexer con due ingressi di selezione e quattro ingressi dati (MUX 4-1):
Di seguito lo schema corrispondente:
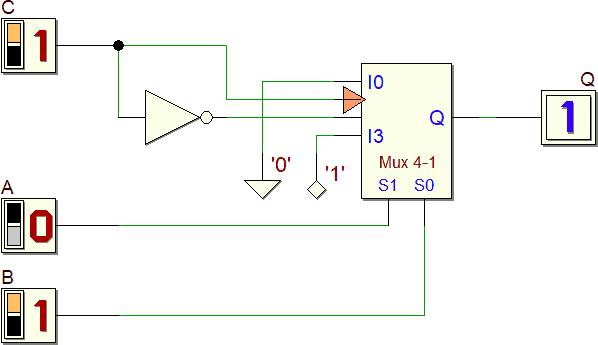
La stessa tabella del precedente esercizio può essere sintetizzata con un MUX 2-1 suddividendo a metà la tabella originale:
| A | B | C | Q | |
| 0 | 0 | 0 | 0 | Q = B · C |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | Q = B + C |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
Il valore di Q nelle singole sottotabelle può essere ricavato con un po' di intuito oppure usando il metodo delle forme canoniche o altre tecniche.
De seguito la realizzazione circuitale:
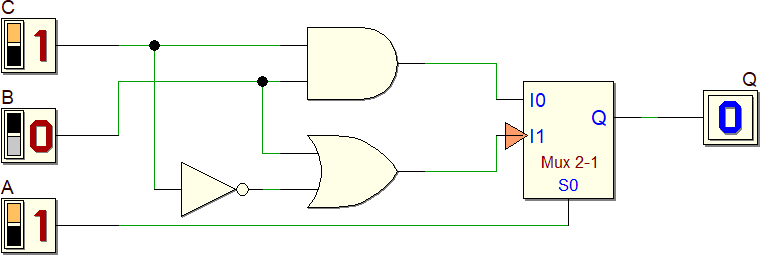
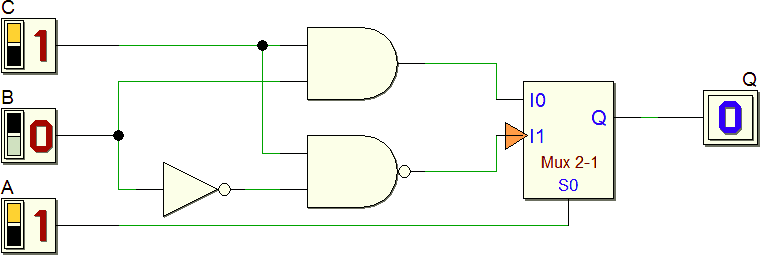
Sono possibile anche altre soluzioni, per esempio la seguente:
Disegnare la rete corrispondente alla seguente tabella usando un multiplexer con 2 ingressi dati e un ingresso di selezione:
| A | B | C | Q |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Per verificare la corretta esecuzione dell'esercizio utilizzare un simulatore digitale come Deeds.
Disegnare la rete corrispondente alla tabella dell'esercizio 5a usando un multiplexer con 4 ingressi dati (due ingressi di selezione).
Disegnare la rete corrispondente alla tabella dell'esercizio 5a usando un multiplexer con 8 ingressi dati (tre ingressi di selezione).
Dalla pagina www.digitalelectronicsdeeds.com...labtopics fare l'esercizio Analysis and design of multiplexer-based combinational networks
Pagina creata nel novembre 2020
Ultima modifica: 13 febbraio 2024
Appunti scolastici - Versione 0.1032 - Maggio 2025
Copyright 2012-2025, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)