In questa pagina descrivo gli elementi base di un circuito digitale sequenziale: latch e flip-flop.
Formalmente un circuito digitale sequenziale è una rete di porte logiche le cui uscite in un certo istante dipendono dal valore logico presente agli ingressi in quello stesso istante e negli istanti precedenti.
In alternativa, possiamo affermare che in una rete sequenziale il valore delle uscite dipende dagli ingressi e dallo stato del circuito, definizione molto simile a quella di un automa di Mealy.
L'immagine di apertura al solito nulla c'entra con il contenuto della pagina. La parte sinistra è riservata a chi comprende l'idioma che si parla(va) dalle mie parti; la parte destra è invece comprensibile a chi preferisce esprimersi, per citare il ragionier Fantozzi, come gli abitanti della perfida Albione.
Consideriamo il seguente circuito, costituito da due porte NOR:
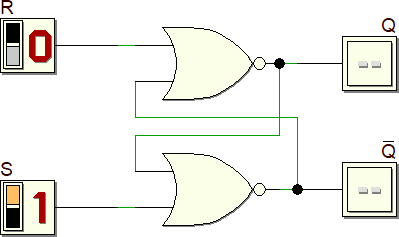
I due ingressi vengono spesso chiamati Set e Reset, con il significato traducibile con imposta (a uno) e ripristina (a zero). Il nome assegnato alle due uscite Q e Q suggerisce che il loro valore è uno opposto all'altro.
Vediamo il funzionamento. Quando gli ingressi R ed S sono diversi, il comportamento sembra tipico di un normale circuito combinatorio:
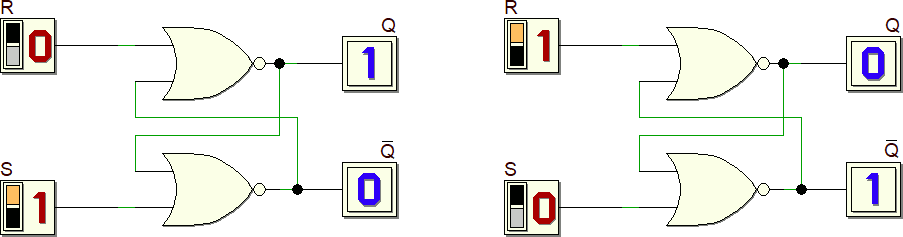
Quando entrambi gli ingressi R ed S sono bassi il valore di Q dipende dall'ordine con cui sono stati precedentemente cambiati gli ingressi R ed S oppure, se vogliamo, dallo stato memorizzato all'interno del circuito.
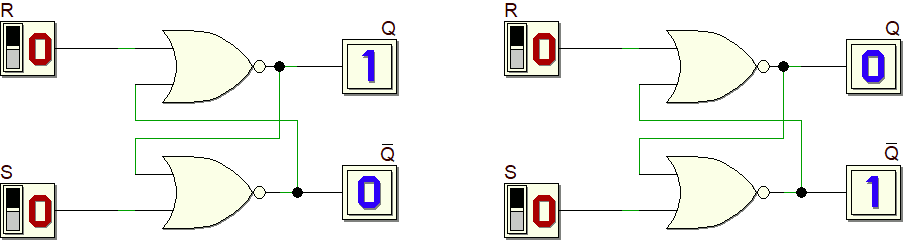
Quello realizzato è spesso indicato come latch SR o anche latch RS (nota 1).
Nelle figure precedenti manca una combinazione degli ingressi (R = 1 e S = 1). Non è riportata perché non utile a livello applicativo in quanto risulta Q = Q; a volte è indicato come stato non persistente (si veda uno dei seguenti esercizi) oppure, spiegazione meno convincente, è indicata come non valida.
Possiamo descrivere questa rete con la seguente tabella di verità:
| R | S | Q | Q | |
| 0 | 0 | Qn-1 | Qn-1 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 0 | nota 3 |
Il simbolo Qn-1 indica il valore precedente di Q, che è stato memorizzato. In altri termini significa che l'uscita rimane invariata.
Possiamo descrivere questa rete con un diagramma temporale:
Osservazioni relative al diagramma temporale:
Sono disponibili come circuiti integrati sia latch R S che latch R S.
Spesso sono presenti ingressi aggiuntivi:
In genere gli ingressi PR e CL sono utilizzati per impostare il valore iniziale memorizzato nel latch. Spesso sono attivi bassi.
Di seguito la tabella di verità di un latch SR con ingresso di Enable attivo alto:
| S | R | En | Q | Q |
| X | X | L | Qn-1 | Qn-1 |
| 1 | 0 | H | 1 | 0 |
| 0 | 1 | H | 0 | 1 |
| 0 | 0 | H | Qn-1 | Qn-1 |
| 1 | 1 | H | 0 | 0 |
Alla pagina www.digitalelectronicsdeeds.com.../labtopics.html sono disponibili i seguenti Labs:
Si analizzi in particolare il funzionamento del latch D, spesso chiamato transparent latch:
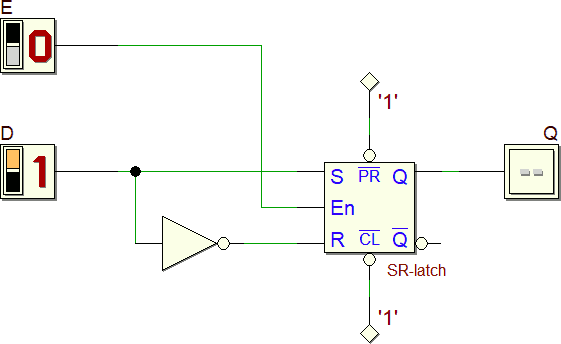
Un chiarimento lessicale (nota 1)
Analizzare i fogli tecnici del 74HC75 (transparent latch) del 74HC279 (latch SR)
Un Flip Flop (FF) è un circuito sequenziale le cui uscite cambiano esclusivamente in corrispondenza di uno dei fronti del segnale di clock CK (nota 2); in corrispondenza dell'altro fronte, del livello alto oppure del livello basso del clock le uscite non cambiano.
Il segnale di clock è evidenziato nel simbolo da un triangolo se il fronte attivo è quello di salita (Positive Edge Triggered, PET o anche Rising Edge triggered) oppure un triangolo ed un cerchio (nota 5) se il fronte attivo è quello di discesa (Negative Edge Triggered, NET o anche Falling Edge triggered)).
Di seguito il simbolo di un Flip Flop JK, tra i vari FF quello forse di impiego più generale:
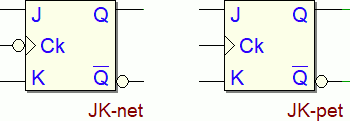
Di seguito la sua tabella di verità, relativa ad un FF JK attivato dal fronte di salita del clock (Positive-edge triggered):
| J | K | CK | Q | Q | |
| X | X | 0 | Qn-1 | Qn-1 | 1 |
| X | X | 1 | Qn-1 | Qn-1 | 2 |
| X | X | ↓ | Qn-1 | Qn-1 | 3 |
| 1 | 0 | ↑ | 1 | 0 | 4 |
| 0 | 1 | ↑ | 0 | 1 | 5 |
| 0 | 0 | ↑ | Qn-1 | Qn-1 | 6 |
| 1 | 1 | ↑ | Qn-1 | Qn-1 | 7 |
Esaminiamo la tabella di verità:
In genere, oltre agli ingressi J e K, sono presenti ingressi asincroni, cioè non sincronizzati dal clock:
PR e CL non possono essere attivi contemporaneamente.
A volte è presente anche un ingresso di Enable (E oppure En) che abilita il funzionamento del FF
Di seguito il simbolo, come presente in Deeds:
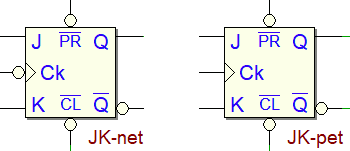
Osserviamo infine il seguente diagramma temporale esemplificativo:
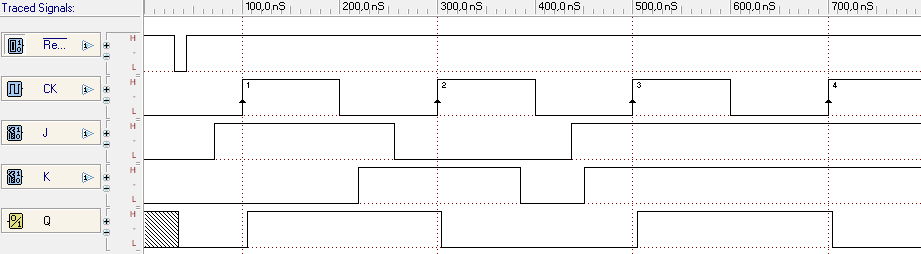
Alla pagina www.digitalelectronicsdeeds.com.../labtopics.html è disponibile il seguente Lab:
Analizzare il seguente circuito e descrivere il suo funzionamento, anche in relazione alla tabella sopra riportata:
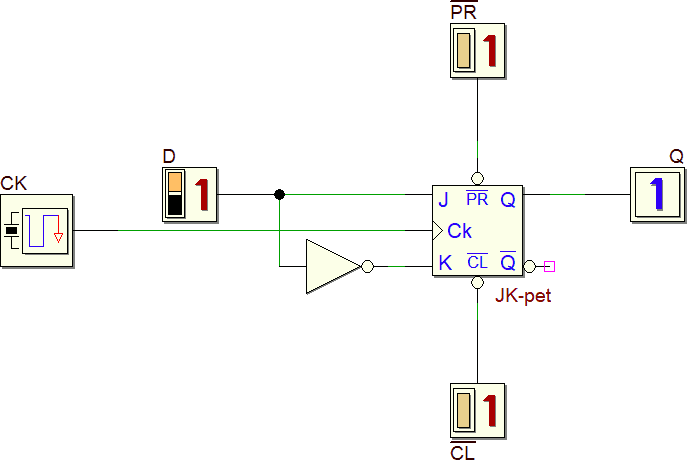
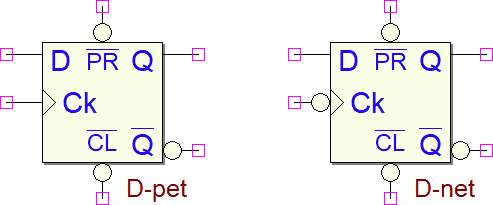
Questa configurazione è di uso piuttosto frequente e indicata come Flip Flop D. Di seguito il simbolo e la tabella di verità relativa a D-pet:
| PR | CL | D | CK | Q | Q |
| 1 | 1 | X | 0 | Qn-1 | Qn-1 |
| 1 | 1 | X | 1 | Qn-1 | Qn-1 |
| 1 | 1 | X | ↓ | Qn-1 | Qn-1 |
| 1 | 1 | 0 | ↑ | 0 | 1 |
| 1 | 1 | 1 | ↑ | 1 | 0 |
| 0 | 1 | X | X | 1 | 0 |
| 1 | 0 | X | X | 0 | 1 |
| 0 | 0 | X | X | - | - |
L'ultima riga (PR e CL attivi contemporaneamente) non è ammessa e produce risultati imprevedibili e/o non significativi
Alla pagina www.digitalelectronicsdeeds.com.../labtopics.html sono inoltre disponibili i seguenti Labs:
Analizzare i fogli tecnici del 74HC112 (FF JK NET) e del 74HC74 (FF D PET).
I due circuiti integrati contenenti latch o FF più utilizzati sono il 74HC373 ed il 74HC374, molto simili tra di loro; gli altri presenti in questa pagina sono piuttosto vecchi e praticamente introvabili sul mercato. Analizzare i fogli tecnici di 74HC373 e 74HC374, individuando le differenze nel loro comportamento.
Pagina creata nel novembre 2020.
Ultima modifica: 2 marzo 2024
Appunti scolastici - Versione 0.1025 - Maggio 2024
Copyright 2012-2024, Vincenzo Villa (https://www.vincenzov.net)
Creative Commons | Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)
